简介:本文介绍了如何使用MATLAB编程语言开发电动汽车续航里程模型,该模型通过分析放电深度(DoD)与行驶距离的关系来预测不同条件下的车辆续航里程。项目首先收集电池规格和性能数据,进行预处理,然后基于驾驶周期分析数据,并通过曲线拟合和插值建立DoD与行驶距离的函数关系。模型结果可以可视化展示,并可扩展考虑其他因素如温度、负载、驾驶风格来提高预测精确度。最后,该模型可用于实际电动汽车的续航预测,以减少驾驶员的“电量焦虑”。附带的ZIP压缩包包含实现该模型的MATLAB脚本和数据文件。 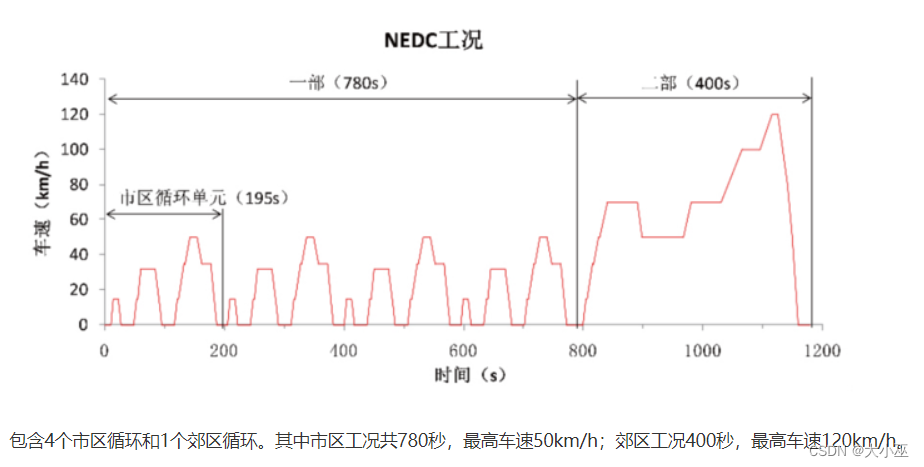
1. 电动汽车续航里程模型开发
在电动汽车技术不断进步的今天,续航里程成为消费者和制造商关注的焦点。为了提高电动汽车的续航能力,开发者和工程师需要深入理解电池放电行为和影响因素。本章将为读者介绍如何开发一个准确的电动汽车续航里程模型,从而为电池管理系统(BMS)优化和车辆设计提供有力的支持。
续航里程模型的开发是一个复杂的过程,它依赖于大量的实验数据和精确的数学建模。我们将首先探讨电池的放电深度(DoD)对行驶距离的影响,随后介绍如何使用MATLAB进行数据处理和分析,并最终构建出一个可视化的预测模型。
模型的准确性和可靠性是至关重要的,因此我们将特别关注于如何通过MATLAB工具箱来提高模型的精度,并在多变的实际驾驶条件中进行测试和验证。本章将为接下来的章节奠定基础,从理论到实践,逐步深入至模型开发的每个细节。
2. 放电深度(DoD)与行驶距离关系分析
2.1 放电深度(DoD)的基本概念
2.1.1 DoD的定义及重要性
放电深度(Depth of Discharge, DoD)是衡量电池在一次放电周期中放电量的参数,它代表了电池容量的利用程度。在电动汽车领域,DoD通常以百分比表示,计算公式为:
[ DoD = \frac{放电量}{总电池容量} \times 100\% ]
DoD的重要性在于它与电池的寿命和性能息息相关。一般情况下,电池的循环寿命与DoD成反比关系,即DoD越大,电池循环次数越少,寿命越短。然而,DoD也是决定电动汽车行驶距离的关键因素之一。电池的全寿命周期中,尽量避免深度放电是延长电池寿命的有效方法。因此,理解DoD对电动汽车续航里程的影响,对设计和优化电池管理系统至关重要。
2.1.2 DoD与电池性能的关系
DoD的大小直接影响电池的可用能量和输出功率。较低的DoD可以提高电池的可循环性,延长其使用寿命,但这通常也意味着每次充电后能够驱动车辆行驶的距离减少。反之,较高的DoD虽然可以提高单次行驶距离,但长期来看会加速电池的老化过程,减少电池的总使用寿命。
在电动汽车的实际使用中,合理地控制DoD值可以平衡续航里程和电池寿命之间的关系,达到最佳的经济效益。此外,DoD还与电池的热管理紧密相关,过度放电可能引起电池过热,影响其安全性和稳定性。因此,电动汽车的电池管理系统(BMS)通常会根据车辆的实际运行状况动态调整DoD值,以确保电池的安全高效工作。
2.2 行驶距离的测量方法
2.2.1 现场测试与数据分析
测量电动汽车行驶距离的最直接方式是现场测试。通过模拟实际驾驶情况,可以记录下电动汽车从完全充电到电量耗尽的全过程,并记录相应的行驶里程。这样的数据对验证电池的标称容量和实际续航能力有重要的参考价值。
数据分析在测试过程中也是不可或缺的一部分。通过对行驶过程中的电压、电流、温度等参数进行记录和分析,可以进一步了解电池在不同驾驶状态下的表现,识别影响续航里程的关键因素。例如,剧烈加速和频繁刹车等驾驶行为会增加能耗,降低行驶距离。数据分析可以通过专业软件进行,但MATLAB等工具提供了强大的自定义分析能力,可以实现更深入的数据挖掘和模式识别。
2.2.2 行驶距离的影响因素
电动汽车的行驶距离除了受到DoD的影响外,还受到多种因素的影响,包括但不限于:
- 车辆负载 :车辆的重量直接影响能耗,载重越大,能量消耗越快。
- 环境温度 :电池在低温环境下性能会下降,影响续航里程。
- 驾驶习惯 :激进的驾驶习惯会导致能耗增加。
- 路况 :不平坦的路面或者爬坡都会增加电池的负担。
- 电池健康状况 :电池老化后容量会下降,影响续航能力。
为了准确地测量行驶距离,测试时应尽量模拟实际使用情况,同时控制上述变量,确保数据的准确性和可重复性。通过多元回归分析等统计方法,研究这些因素如何独立及相互作用地影响续航里程,对于优化电池性能和提高电动汽车的整体效能具有重要的指导意义。
3. MATLAB数据分析和图形化功能应用
3.1 MATLAB在数据处理中的作用
3.1.1 数据输入和预处理步骤
在进行电动汽车续航里程的分析时,数据的输入和预处理是至关重要的步骤。数据的准确性直接影响到后续分析和模型构建的质量。MATLAB提供了多种数据输入方式,包括但不限于手动输入、读取外部文件(如CSV、Excel文件等)、数据采集接口等。数据预处理的步骤通常包括数据清洗、数据标准化、缺失值处理和数据归一化等。在MATLAB中,可以通过编写脚本自动完成这些预处理步骤,提高效率。
% 示例代码:数据输入和预处理
% 假设有一个CSV文件,包含电动汽车的行驶数据
filename = 'electric_vehicle_data.csv';
% 读取CSV文件数据
data = readtable(filename, 'Delimiter', ',', 'ReadVariableNames', true);
% 数据预处理,例如处理缺失值
data(ismissing(data)) = median(data, 'omitnan');
% 数据标准化
data.StandardizedData = (data.Var1 - mean(data.Var1)) / std(data.Var1);
在上述代码中,我们首先读取了一个CSV文件,并处理了其中的缺失值。然后,我们选取了文件中的一个变量 Var1 进行标准化处理。这样处理后的数据可以用于进一步的分析和图形化展示。
3.1.2 数据分析方法和MATLAB工具箱
MATLAB提供了丰富的数据分析方法和工具箱,如统计工具箱(Statistics and Machine Learning Toolbox),它为用户提供了大量用于数据分析和机器学习的函数和算法。这些工具箱可以进行描述性统计、假设检验、回归分析、分类、聚类等多种分析方法。此外,MATLAB还支持自定义算法开发,方便研究人员进行更深入的数据分析。
% 示例代码:使用统计工具箱进行描述性统计分析
meanDistance = mean(data.StandardizedData);
medianDistance = median(data.StandardizedData);
stdDistance = std(data.StandardizedData);
% 输出结果
fprintf('平均行驶距离:%f\n', meanDistance);
fprintf('中位数行驶距离:%f\n', medianDistance);
fprintf('标准差行驶距离:%f\n', stdDistance);
以上代码计算了标准化数据的平均值、中位数和标准差。这些基本的统计信息对于理解数据集的基本特性至关重要。
3.2 MATLAB图形化界面的创建
3.2.1 图形化界面设计原则
在设计MATLAB的图形化界面时,应遵循一些基本原则,以确保界面的友好性和易用性。这些原则包括:简洁性(界面应避免过多的元素和信息过载),直观性(用户应能一目了然地理解如何操作界面),一致性(界面的各个部分和操作应保持一致性,以便用户学习和使用),及时反馈(用户操作后应有明确的反馈)以及容错性(设计应能减轻或避免用户的误操作)。在MATLAB中,可以通过App Designer工具来创建符合这些原则的图形化用户界面(GUI)。
3.2.2 利用MATLAB绘制放电深度与行驶距离图
MATLAB的图形化功能非常适合于快速绘制数据图表。对于研究放电深度(DoD)与行驶距离之间的关系,MATLAB提供了一整套绘图函数,可以轻松地将数据可视化。下面的示例代码展示了如何使用MATLAB绘制放电深度与行驶距离的关系图。
% 示例代码:绘制放电深度(DoD)与行驶距离的关系图
% 假设data中包含DoD和Distance两个变量
plot(data.DoD, data.Distance);
xlabel('放电深度 (DoD)');
ylabel('行驶距离');
title('放电深度与行驶距离关系图');
grid on;
在这段代码中,我们使用了plot函数将DoD数据和Distance数据绘制成线图。通过x轴和y轴的标签以及标题,用户可以清楚地了解到图表所表达的关系。MATLAB的图形化功能不仅限于线图,还支持柱状图、散点图、曲面图等多种类型的图表,非常适合于数据的可视化分析。
4. 驾驶周期对能耗和DoD影响的分析
4.1 驾驶周期的定义和分类
4.1.1 常见驾驶周期介绍
驾驶周期是定义一系列行驶速度和时间数据的组合,它代表了车辆在现实世界中的驾驶情况。一个典型的驾驶周期包含加速、匀速、减速和停车等阶段,用以模拟车辆在日常行驶中的能量消耗和排放情况。常见的驾驶周期有:
-
城市行驶周期(Urban Driving Cycle) :此周期主要模拟城市中的交通状况,包含了频繁的启停和低速行驶。例如,美国的FTP-72城市驾驶周期,以及欧洲的NEDC(New European Driving Cycle)。
-
公路行驶周期(Highway Driving Cycle) :公路驾驶周期则关注在较为理想的交通条件下,车辆的行驶状态。例如,美国的Highway Fuel Economy Test(HWFET)。
-
全球轻型车辆测试程序(WLTP) :WLTP是最新提出的国际标准化测试程序,旨在更准确地反映现代车辆在各种行驶条件下的能耗和排放水平。
4.1.2 驾驶周期与能耗的关联
驾驶周期的不同会影响车辆的能耗,因为它决定了电池放电的深度以及放电速率。驾驶周期内包含的启停次数越多、速度变化幅度越大,则能耗越高。同时,对于电动汽车而言,驾驶周期影响行驶距离的一个重要因素是放电深度(DoD)。
放电深度是指电池从满电状态到当前状态所释放出的能量百分比。高放电深度通常意味着更高的能耗和续航里程的减少。因此,研究驾驶周期对能耗和DoD的影响,对于电动汽车的续航里程预测模型至关重要。
4.2 分析驾驶周期影响的MATLAB实现
4.2.1 驾驶周期数据的采集和处理
为了研究不同驾驶周期对能耗和DoD的影响,首先需要采集相关数据。数据采集可以通过车载传感器进行,也可以使用专业的测试仪器进行模拟驾驶周期的测试。
数据处理包括数据清洗、数据归一化等步骤。数据清洗的目的是去除不合理的数据点,比如速度超出了正常的行驶范围。数据归一化则使得不同驾驶周期下的数据能够在相同的基准下进行比较。
以下是一个简化的MATLAB代码示例,用于处理和归一化驾驶周期数据:
% 假设data为原始采集的驾驶周期数据,其列包括时间(s)、速度(km/h)、加速度(m/s^2)
% 首先进行数据清洗,排除不合理数据点
valid_idx = data(:,1) > 0 & data(:,2) >= 0 & data(:,2) <= 100;
clean_data = data(valid_idx, :);
% 进行数据归一化处理,例如速度数据归一化至0-1范围
speed_normalized = (clean_data(:,2) - min(clean_data(:,2))) / (max(clean_data(:,2)) - min(clean_data(:,2)));
% 将处理后的数据保存至新变量中,用于进一步分析
normalized_data = [clean_data(:,1), speed_normalized, clean_data(:,3)];
4.2.2 MATLAB脚本分析驾驶周期对DoD的影响
接下来,我们可以通过MATLAB编写脚本来分析驾驶周期对DoD的影响。脚本的关键在于模拟电池放电过程,并计算在不同的驾驶周期下的DoD。
以下是一个简化的MATLAB脚本示例,用于模拟电池放电过程并计算DoD:
% 假设batteryCapacity为电池容量,Ah(安时),initialStateOfCharge为初始荷电状态,百分比
% 使用循环模拟驾驶周期的每个阶段
SoC = initialStateOfCharge;
for cycle_idx = 1:size(normalized_data, 1)
% 根据时间差计算每个阶段的持续时间
delta_time = normalized_data(cycle_idx, 1);
% 根据速度和加速度估计能耗(假设能耗与速度和加速度成正比)
energyConsumed = delta_time * (normalized_data(cycle_idx, 2)^2 + normalized_data(cycle_idx, 3)^2);
% 更新荷电状态(SoC)
SoC = SoC - energyConsumed / batteryCapacity;
% 计算当前的DoD
DoD = 100 * (1 - SoC);
% 可以将每个阶段的DoD输出到文件或绘制图形
end
通过上述MATLAB脚本,我们可以得到不同驾驶周期下,电池的放电深度变化情况。在实际分析中,还可以引入更多复杂的因素,比如温度、车辆负载等,以得到更精确的结果。
在下一章中,我们将进一步讨论如何利用曲线拟合和插值技术在MATLAB中对这类数据进行更加细致的分析。
5. 利用MATLAB进行曲线拟合和插值
5.1 曲线拟合的基本原理和方法
5.1.1 曲线拟合的数学模型
曲线拟合是数据分析和科学计算中的一项基本技能,用于找出两个变量之间的关系,这种关系可以通过数学函数的形式来表达。具体来说,它尝试找到最适合一组观测数据点的曲线方程,通常是在最小二乘意义上寻找最佳拟合曲线,以最小化预测值和实际数据点之间的差异。
常见的曲线拟合模型包括线性回归、多项式回归、指数回归等。每种模型都有其适用情况和局限性。线性回归是基础且最简单的模型,适合数据点分布呈现直线关系时使用。多项式回归通过一个或多个自变量的高次幂来适应数据,适合曲线拟合;但其系数数量随着次数的提高而大幅增加,导致模型变得复杂和过拟合。指数回归通常用于处理呈指数增长或衰减的数据集。
5.1.2 MATLAB中曲线拟合工具箱的使用
MATLAB提供了强大的曲线拟合工具箱(Curve Fitting Toolbox),可以方便地进行各类数据的曲线拟合工作。工具箱中包含了诸如拟合、绘图、评估拟合优度等一系列函数,用户可以根据具体需求选择合适的函数进行操作。
拟合过程通常分为以下几步: 1. 数据准备:将需要拟合的数据导入MATLAB中,准备进行处理。 2. 选择模型:确定拟合的模型类型,比如多项式、高斯、指数等。 3. 进行拟合:使用MATLAB的 fit 函数进行曲线拟合操作。 4. 分析结果:通过拟合得到的模型函数,用以预测或分析其他数据。 5. 优化和验证:通过相关统计指标如R平方、均方误差等对模型进行验证和调整。
下面是一个简单的代码块,展示如何使用MATLAB进行一次简单的线性拟合:
% 假定有一组数据点x和y
x = [1, 2, 3, 4, 5];
y = [2, 3, 5, 7, 11];
% 使用MATLAB的fit函数进行线性拟合
[p, s] = fit(x', y', 'poly1'); % 'poly1'代表线性拟合
% p为拟合得到的模型参数,s为拟合结果的统计信息
% 然后可以使用p和拟合函数对新的数据点进行预测
在此代码中, fit 函数使用了多项式模型中的'poly1',即一次多项式(线性回归)。函数返回参数 p (模型参数)和 s (拟合统计信息)。这些参数可以用于进一步分析或预测新数据点的值。
通过曲线拟合,我们可以得到电池放电深度与行驶距离之间的关系模型,进而对电动汽车的续航能力进行预测。但需要注意,拟合得到的模型并不能保证在所有情况下都是准确的,特别是在超出已有数据范围的情况下。因此,进行模型验证和精度评估是非常必要的。
5.2 插值技术的原理及MATLAB实现
5.2.1 插值的基本概念和种类
插值是数学中一种重要的数值分析手段,它用来估计两个已知数据点之间未知数据点的值。基本原理是假设数据点之间存在某种连续性,通过已知点来推算未知点的值。
插值方法有很多种,包括线性插值、多项式插值、样条插值等。线性插值是最简单的插值方法,通过两个相邻数据点之间画直线来估计未知值,适合数据变化比较平滑的情况。多项式插值使用多项式函数通过所有已知数据点,适用于数据变化复杂的情况,但可能会导致龙格现象。样条插值则使用分段多项式,通过每个数据点并满足一定的平滑性条件,它在避免过拟合和维持平滑性方面有很好的表现。
5.2.2 MATLAB中的插值函数和应用
MATLAB提供了多种插值函数,例如 interp1 、 interp2 、 interp3 和 spline 等。这些函数可以处理一维、二维甚至三维数据的插值。
以 interp1 函数为例,它可以对一维数据进行插值。使用示例如下:
% 已知数据点
x = [1, 2, 3, 4];
y = [1, 4, 9, 16];
% 进行插值,求解x=2.5时的y值
xq = 2.5;
yq = interp1(x, y, xq, 'linear');
% 输出插值结果
disp(['插值结果为: ', num2str(yq)]);
在这个例子中, interp1 函数使用了线性插值方法(由参数'linear'指定), xq 是我们要查询的点。函数返回了 xq 对应的 y 值 yq 。MATLAB中还有其他参数可以用来指定不同的插值方法,以及控制插值的精度和平滑度。
插值技术在电动汽车的续航里程预测模型中有广泛应用。例如,通过已知的电池放电深度(DoD)和行驶距离数据,我们可以利用插值技术计算出在任意DoD值下对应的预测行驶距离,从而增强模型的预测能力和适应性。
此外,在MATLAB中进行插值时,还可以通过创建图形化的用户界面(GUI),使用户能够通过图形交互式地选择数据点和插值方法,从而进行更加直观和方便的数据分析。在下一章节中,我们将深入讨论如何利用MATLAB创建图形化界面,并在驾驶周期影响分析的背景下展示如何实现这一过程。
6. 续航里程预测模型的可视化展示
续航里程是电动汽车用户和制造商最关心的性能指标之一。为了更直观地理解和展示续航里程预测模型,这一章节将详细介绍如何构建、验证预测模型,并使用MATLAB工具将其结果可视化。模型的构建和验证是后续可视化的基础,而可视化技术的运用则能够提供直观的视觉效果,从而帮助用户和决策者更好地理解和应用模型。
6.1 预测模型的构建和验证
构建准确的续航里程预测模型是实现有效可视化展示的前提。在这个过程中,我们需要确保模型能够准确反映电池放电特性、车辆动力学、环境条件等要素对续航里程的影响。
6.1.1 模型的数学表达和构建步骤
续航里程预测模型的构建首先需要明确其数学表达式。这通常包括基于物理或经验的电池放电模型、车辆行驶的动力学模型、以及可能影响续航里程的环境因素模型。一个基本的模型构建步骤可能包含以下部分:
- 数据采集:收集历史行驶数据,包括电池状态、驾驶模式、环境条件等。
- 数据分析:分析数据,确定模型的主要影响因素。
- 参数估计:利用数据估计模型参数,可以采用回归分析、机器学习等方法。
- 模型验证:用测试数据集对模型进行验证,确保其预测精度。
6.1.2 模型的验证方法和标准
模型验证是确保模型预测能力的重要环节。常用的验证方法包括:
- 划分数据集为训练集和测试集,利用训练集进行模型训练,用测试集对模型进行评估。
- 使用交叉验证方法确保模型对数据集具有更好的泛化能力。
- 计算模型预测结果与实际数据之间的误差,常用的统计指标包括均方误差(MSE)和决定系数(R²)。
6.2 模型结果的可视化技术
模型构建完成后,我们需要将模型结果以直观的方式展示给用户。有效的可视化不仅可以帮助用户理解模型的预测结果,而且有助于进行进一步的分析和决策。
6.2.1 高效的图形展示方法
高效的图形展示方法可以包括:
- 曲线图:展示续航里程随时间或行驶距离的变化情况。
- 散点图:显示不同条件下的实际续航里程与预测续航里程的对比。
- 热力图:展示不同环境条件和驾驶模式对续航里程影响的热力分布。
6.2.2 MATLAB中实现模型结果的可视化
在MATLAB中实现模型结果的可视化,我们可以使用以下方法:
% 假设我们有模型预测的续航里程数据和实际测量数据
predictedRange = [250, 280, 300, 290, 270]; % 预测续航里程
actualRange = [245, 275, 310, 280, 265]; % 实际续航里程
% 创建一个图表窗口
figure;
% 绘制散点图,展示预测值和实际值
scatter(1:length(predictedRange), predictedRange, 'b', 'filled');
hold on;
scatter(1:length(actualRange), actualRange, 'r', 'filled');
% 添加图例和标题
legend('预测续航里程', '实际续航里程');
title('续航里程预测与实际对比');
xlabel('测试案例');
ylabel('续航里程 (公里)');
% 显示网格
grid on;
% 保持图形
hold off;
通过上述MATLAB代码块,我们可以生成一张直观的散点图来对比预测续航里程与实际测量结果。这样的图形展示方法便于理解模型的有效性,为进一步优化模型提供了直观的参考。
在后续的章节中,我们将讨论如何将影响续航里程的其他因素考虑进去,并对模型进行扩展与优化。
简介:本文介绍了如何使用MATLAB编程语言开发电动汽车续航里程模型,该模型通过分析放电深度(DoD)与行驶距离的关系来预测不同条件下的车辆续航里程。项目首先收集电池规格和性能数据,进行预处理,然后基于驾驶周期分析数据,并通过曲线拟合和插值建立DoD与行驶距离的函数关系。模型结果可以可视化展示,并可扩展考虑其他因素如温度、负载、驾驶风格来提高预测精确度。最后,该模型可用于实际电动汽车的续航预测,以减少驾驶员的“电量焦虑”。附带的ZIP压缩包包含实现该模型的MATLAB脚本和数据文件。
























 302
302

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








