动态规划（js）

基本思想：

主要是一种迭代的思想，将大问题划分成为若干个子问题，并将子问题保存起来，找到问题之间的递推公式并求得最终解，常用来求解最优解问题，递归分治也是将大问题划分成小问题并求得最终解的思想，它与动态规划的区别在于前者主要解决划分不相交的子问题，而后者的子问题往往是相交的，如果这时候用递归会造成很多的重复运算，动态规划是一种牺牲空间换时间的算法。

例题：

斐波那契数列

描述

输入描述：

一个正整数n

返回值描述：

输出一个正整数。

示例1

输入：4

返回值：3

说明：根据斐波那契数列的定义可知，fib(1)=1,fib(2)=1,fib(3)=fib(3-1)+fib(3-2)=2,fib(4)=fib(4-1)+fib(4-2)=3，所以答案为3。

递归解法：

function Fibonacci(n)
{
    if(n == 1) {
        return 1;
    } else if(n == 2) {
        return 1;
    } else {
        //这里会造成很多重复计算，时间复杂度2的n次方
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}

动态规划：

function Fibonacci(n)
{
    let dp = [];
    dp[1] = 1;
    dp[2] = 1;
    for(let i = 3; i <= n; i ++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

这是一个很典型的问题，同时题目也告诉了我们递推公式：dp[i]=dp[i-1]+[i-2]，dp[i]表示输出斐波那契数列的第i项，我们的dp[i-1]和dp[i-2]此时已经保存在数组中了，因此直接可以得到最终结果，时间复杂度为n。

跳台阶

描述

示例1

function jumpFloor(n)
{
    let dp = [];
    dp[1] = 1;
    dp[2] = 2;
    for(let i = 3; i <= n; i ++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

思路：

要求n级台阶总共有多少种跳法，可以把这个大问题划分成小问题，首先定义一个dp数组，用来保存小问题的解，dp[i]表示上i个台阶总共有多少种跳法，我们最终要求dp[n]，那肯定要找它的递推公式，这是每一个动态规划算法的核心所在，要找递推公式，那肯定是要有初始值的，不然怎么递推，这里我们可以从最小的问题开始想，假设只有1级台阶此时只有一种跳法，那么dp[1]=1，当有2级台阶时dp[2]=2，这俩很容易得到的就是初始值，接下来要求dp[3]，一直到dp[n]，这里就要用递推公式了，假设有n级台阶，当青蛙从第1级开始选择跳1阶的时候，那么后面就还有n-1个台阶，n-1个台阶总共有dp[n-1]种跳法，当青蛙从第1级开始选择跳2阶的时候，那么后面还有n-2个台阶，n-2个台阶总共有dp[n-2]种跳法，青蛙是从第1级开始选择跳的，它只能选择跳1阶或者2阶作为开始，那么当有n个台阶时总共有dp[n-1]+dp[n-2]种跳法，即dp[n]=dp[n-1]+dp[n-2]，这就是我们推导出来的递推公式，然后在循环中把dp[3]直到dp[n]全都存起来，最终就得到了我们想要的结果，时间复杂度n

最小花费爬楼梯

描述

示例1

示例2

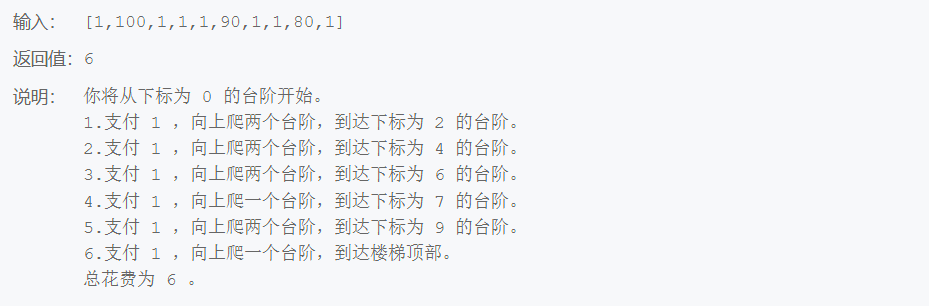
function minCostClimbingStairs( cost ) {
    let len = cost.length;
    let dp = [];
    dp[0] = 0;
    dp[1] = 0;
    for(let i = 2; i <= len; i ++) {
        dp[i] = Math.min((dp[i-2]+cost[i-2]),(dp[i-1]+cost[i-1]));
    }
    return dp[len];
}

思路：

首先建立有一个dp数组存值，dp[i]表示前i个台阶并爬到楼顶的最小花费，然后找它的递推公式，这里分两种情况，一种是上到第i-1个台阶，再往上上两阶台阶到达楼顶，那么第i-1个台阶作为开始要加上一个它的花费（cost[i-2]）,（因为它作为i-2个台阶的楼顶）要计算的是dp[i-2] + cost[i-2]，这是到达i个台阶楼顶的一种情况，另外一种情况是第i个台阶作为开始（意味着它是i-1个台阶的楼顶），再往上上一阶到达楼顶要计算的是dp[i-1]+cost[i-1]，所以i个台阶的最小花费是这两种情况的最小值，因此递推公式是dp[i] = Math.min((dp[i-2]+cost[i-2]),(dp[i-1]+cost[i-1]))。

最长公共子序列(二)

描述

示例1

示例2

function LCS( s1 ,  s2 ) {
    let arr1 = [...s1];
    let arr2 = [...s2];
    let arr = new Array(s1.length+1).fill('').map(() => {return new Array(s2.length+1).fill('')});
    for(let i = 1; i <= arr1.length; i ++) {
        for(let j = 1; j<= arr2.length; j ++) {
            if(arr1[i-1] == arr2[j-1]) {
                arr[i][j] = arr[i-1][j-1] + arr1[i-1];
            } else {
                let str = arr[i-1][j].length >= arr[i][j-1].length ? arr[i-1][j] : arr[i][j-1];
                arr[i][j] = str;
            }
        }
    }
    
    return arr[s1.length][s2.length] == '' ? -1 : arr[s1.length][s2.length];
}

思路：

使用动态规划，先定义二维数组用来保存要迭代的内容，arr[i][j]表示字符串1的前i个字符和字符串2的前j个字符中的最长公共子序列，我这个二维数组是从下标为1开始存的，所以多申请一个空间，思路是可以让两个字符串中的每一个字符做比较，如果相等就等于主对角线元素加上这个字符，如果两个字符串的i和j不相等，就取arr[i][j-1]和arr[i-1][j]中的最大值

这是这两个字符串求最长公共子序列的比较过程，可以看到，行和列的最后一个元素就是最长公共子序列，当然题目中说明仅仅有一个最长公共子序列，所以你可以弄俩字符串自己填下矩阵，是一样的，所以递推公式是：如果arr1[i-1] == arr2[j-1]（下标是从1开始的所以减1），那么 arr[i][j] = arr[i-1][j-1] + arr1[i-1]，否则arr[i][j] =arr[i-1][j].length >= arr[i][j-1].length ? arr[i-1][j] : arr[i][j-1]，初始值就是边界上的那些空字符串，它们在定义二维数组的时候就已经初始化过了。两个字符串各自从前往后出字符那么这个公共字符就保存在主对角线上，如果不相等，比如上图中的第5行和第5列自然要比较abc和bc这俩字符串的最长公共子序列和ab和bca的最长公共子序列哪个最长并保存，时间复杂度n的平方。

最长回文子串

描述

示例1

示例2

示例3

function getLongestPalindrome(str) {
  let arr = [...str];
  let max = 1;
  let dp = new Array(arr.length + 1).fill(0).map((item) => { return new Array(arr.length + 1).fill(0) });
  for (let i = 1; i <= arr.length; i++) {
    dp[i][i] = 1;
  }
  //i从后往前去迭代，直到i=1 j=arr.length填满矩阵的所有内容，就可以得出整个字符串的最长回文子串，时间复杂度n的平方
  for (let i = arr.length - 1; i > 0; i--) {
    for (let j = i + 1; j <= arr.length; j++) {
      if (arr[i - 1] == arr[j - 1]) {
        if (j - i <= 2) {
          dp[i][j] = 1;
          if (j - i + 1> max) {
            max = j - i + 1;
          }

        } else {
          dp[i][j] = dp[i + 1][j - 1];
          if (dp[i][j] == 1) {
            if (j - i + 1> max) {
              max = j - i + 1;
            }
          }
        }
      } else {
        dp[i][j] = 0;
      }
    }
  }
  return max;
}

思路：

这里使用动态规划，可以列二维数组画矩阵，dp[i][j]表示从i到j的子串是不是回文，是则填1否则填0，只需要判断i所对应的元素和j所对应的元素是否相等，如果相等看dp[i+1][j-1]（字符串i到j的掐头去尾子串）是不是相等，如果相等那么dp[i][j]是回文子串，否则它不是，每次当两头相等的时候都用max记录字符串长度并不断更新，这个就是它最长回文子串的长度。

总结

动态规划最主要最难的就是找到它的递推方法即前后之间的状态关系，这个只能多练习勤思考