机器学习之逻辑回归（二）

逻辑回归

线性回归模型的作用是来预测，如果我们的任务是分类呢，可以对线性回归模型进行改造，找一个单调可微的函数将输出值转换为0/1，从而达到分类的效果。对数几率函数是一个常用的这样的函数，$y=\frac{1}{1+e-x}$,图像如下，函数处处可微，且函数值处于0-1之间，

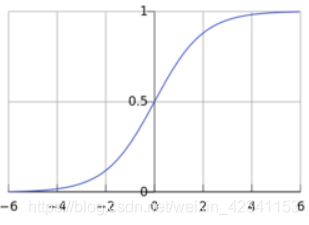
这样我们的函数模型可以写作：

$$y=\frac{1}{1+e^{-(w^{T}x+b)}}$$

上式可以变化为：

$$ln\frac{y}{1-y}=w^{T}x+b$$

若将y视为样本x作为正例的可能性，1-y是反例可能性，两者的比值称为“几率”（odds），反映了x作为正例的相对可能性。

我们通过“极大似然法”来估计w和b，给定数据集${(x_i,y_i)}_{i=1}^m$,对数回归模型最大化“对数似然”

$$l(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)$$

即令每个样本属于其真实标记的概率越大越好，为便于讨论令$\beta =(w:b)$，$\hat{x}=(x;1)$,则$w^{T}x+b$ 可写作${\beta }^T\hat{x}$，再令$p_1(\hat{x};\beta )=p(y=1|\hat{x};\beta )$,$p_0(\hat{x};\beta )=p(y=0|\hat{x};\beta )=1-p_1(\hat{x};\beta )$,则上式后面的似然项可写作：

$$p(y_i|x_i;w,b)=y_i{p}_1(\hat{x};\beta )+(1-y_i)p_0(\hat{x};\beta )$$

将其带入得：

$$l(\beta )=\sum _{i=1}^m(-y_i{\beta }^T\hat{x}+ln(1+e^{{\beta }^T\hat{x}}))$$

上式是一个凸函数，因此可以用梯度下降的方法求得最优解：

$${\beta }^{\ast }={\mathrm{argmin}}_{\beta }l(\beta )$$

以牛顿法为例：

$${\beta }^{t+1}={\beta }^t-(\frac{{\partial }^{2}l(\beta )}{\partial \beta \partial {\beta }^T}{)}^{-1}\frac{\partial l(\beta )}{\partial \beta }$$

其中一二阶导数分别为：

$$\frac{\partial l(\beta )}{\partial \beta }=-\sum _{i=1}^m\widehat{x_i}(y_i-p_1(\widehat{x_i};\beta ))$$

$$\frac{{\partial }^{2}l(\beta )}{\partial \beta \partial {\beta }^T}=\sum _{i=1}^m\widehat{x_i}{\widehat{x_i}}^T{p}_1(\widehat{x_i};\beta )(1-p_1(\widehat{x_i};\beta ))$$

以上；