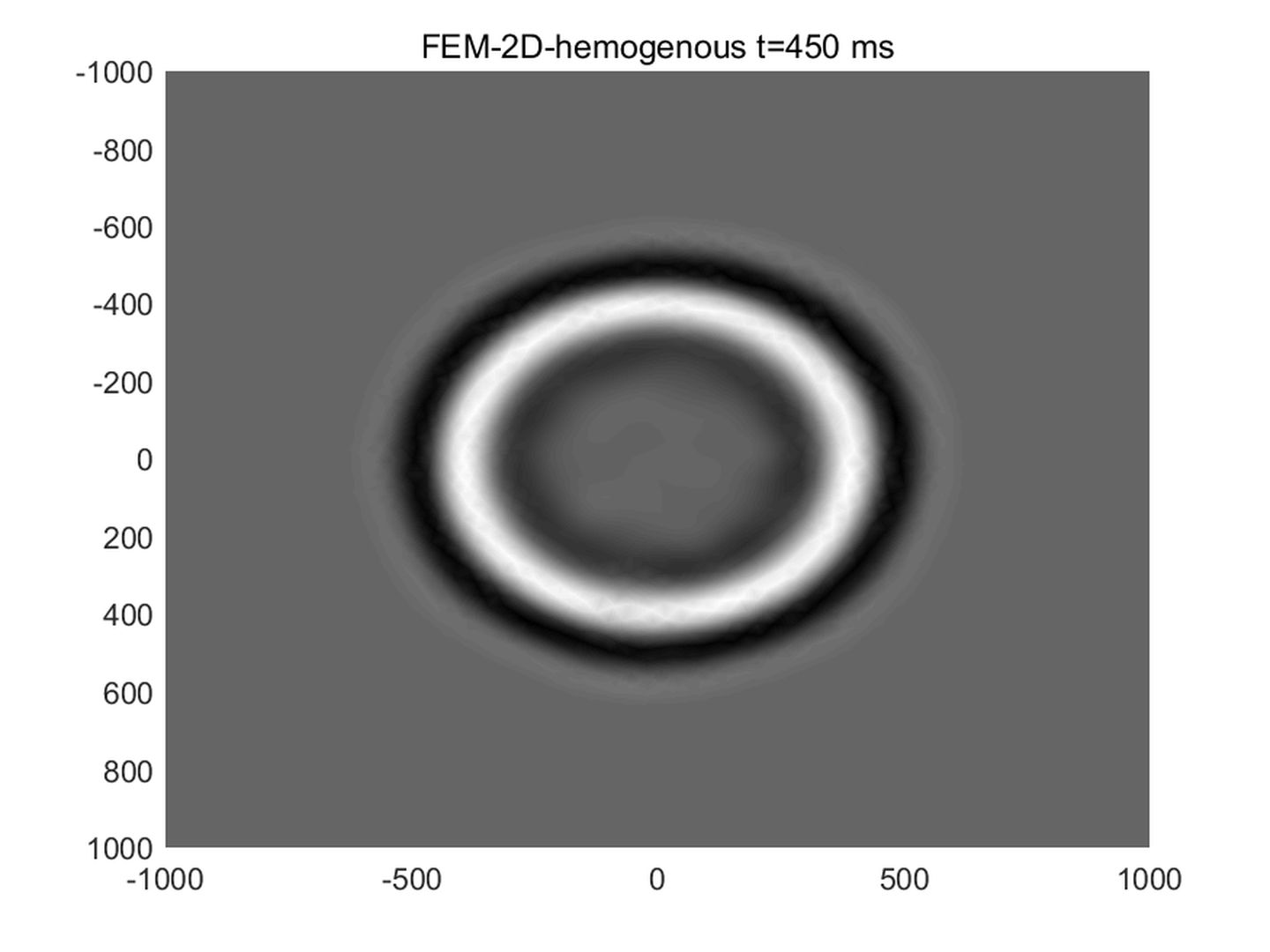
2.1 前言
承接上一篇文章,前面我们已经介绍了一维声波方程有限元求解:
蓝不是蓝:有限单元法(Finite Element Method)实现声波方程模拟(Part 1)zhuanlan.zhihu.com
这一部分将一维问题提升到二维问题。不知道大家有没有发现,在一维问题中,我们是通过矩阵相乘的方式来求解,得到的解
2.2 二维声波方程有限元求解
2.2.1 算法推导
对于二维声波方程,我们先写成一个简写形式:
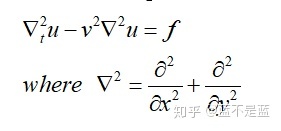
我们同样使用伽辽金(Galerkin )方法将该微分方程变成弱形式。并引入一个二维基函数
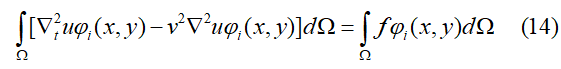
对上式关于空间项的积分使用分部积分法则:
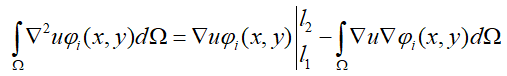
将上式代入公式(14)后得到:
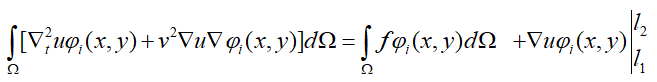
这里我们仍然使用一维情况下类似的边界条件:
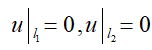
消掉边界条件这一项后,再利用基函数插值近似我们的解(
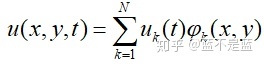
最终得到的公式为:
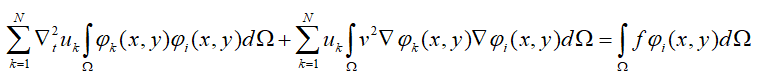
时间项我们采用二阶差分格式,则上式的隐式差分格式为:
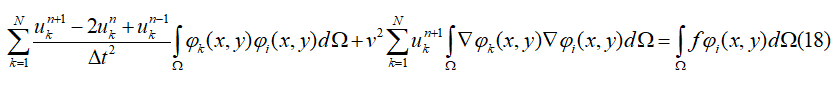
简写成矩阵形式:
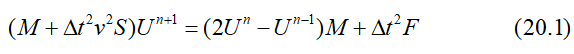
同样的,简写成矩阵形式的显式差分格式为:
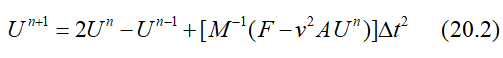
其中的质量矩阵
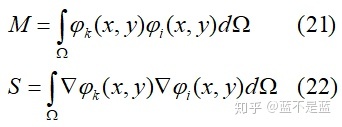
那么,我们先利用公式(21)和(22)求出
2.2.2 网格剖面
在这里我们使用三角形单元构建一个非结构化网格,事实上如果让我们自己来构建一个很复杂的非结构化网格是比较费力的,我们可以使用MATLAB自带的网格生成函数来帮助我们完成网格生成。
这部分代码为:
function [p,e,t] = unstructured()
[p, e, t] = initmesh('squareg', 'hmax', 0.08);%单元初始化
[p,e,t] = refinemesh('squareg',p,e,t);%单元加密
end其中
| 返回值 | 含义 |
|---|---|
| p | 在点矩阵p中,第一行和第二行包含网格中节点编号对应的x和y坐标。 |
| e | 在边界矩阵e中,第一行和第二行包含每一段边界起始点和结束点的索引,第三和第四行包含起始和结束参数值,第五行包含边界段编号,第六和第七行包含左侧和右侧子域编号。 |
| t | 在三角形单元矩阵t中,前三行包含三角形三个角点的索引,按逆时针顺序给出,第四行包含子域编号。 |
上述代码生成的网格为:
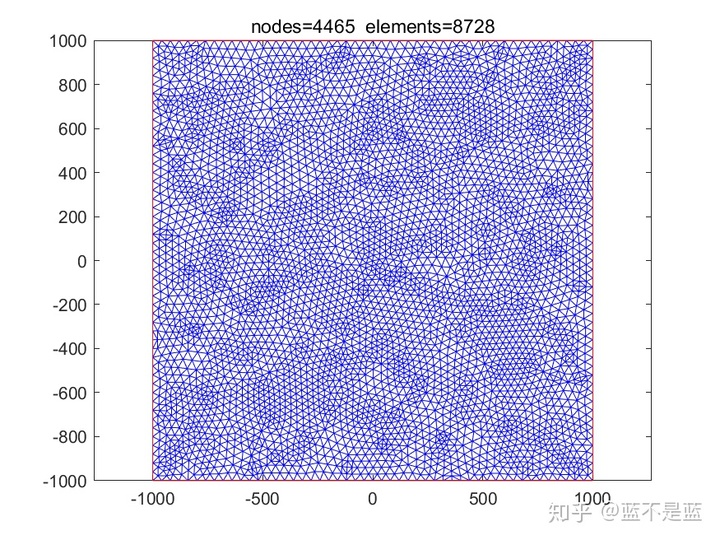








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3367
3367











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








