2020年CSP-J-T1-优秀的拆分(power)
题目描述
一般来说,一个正整数可以拆分成若干个正整数的和。例如,1 = 1,10 = 1 + 2 + 3 + 4等。
对于正整数n的一种特定拆分,我们称它为“优秀的”,当且仅当在这种拆分下,n被分解为了若干个不同的2的正整数次幂。
注意,一个数x能被表示成2的正整数次幂,当且仅当x能通过正整数个2相乘在一起得到。
例如,10 = 8 + 2 = 2^3 + 2^1 是一个优秀的拆分。但是,7 = 4 + 2 + 1 = 2^2 + 2^1 + 2^0就不是一个优秀的拆分,因为1不是2的正整数次幂。
现在,给定正整数n,你需要判断这个数的所有拆分中,是否存在优秀的拆分。若存在,请你给出具体的拆分方案。
输入格式
输入文件名为 power.in。
输入文件只有一行,一个正整数n,代表需要判断的数。
输出格式
输出文件名为 power.out。
如果这个数的所有拆分中,存在优秀的拆分。那么,你需要从大到小输出这个拆分中的每一个数,相邻两个数之间用一个空格隔开。
可以证明,在规定了拆分数字的顺序后,该拆分方案是唯一的。
若不存在优秀的拆分,输出“-1”(不包含双引号)。
输入输出样例
输入样例1:
6
输出样例1:
4 2
输入样例2:
7
输出样例2:
-1
说明
【样例 1 解释】
6 = 4 + 2 = 2^2 + 2^1是一个优秀的拆分。注意,6 = 2 + 2 + 2不是一个优秀的拆分,因为拆分成的3个数不满足每个数互不相同。
【数据范围与提示】
对于20%的数据,n ≤ 10。
对于另外20%的数据,保证n为奇数。
对于另外20%的数据,保证n为2的正整数次幂。
对于80%的数据,n ≤ 1024。
对于100%的数据,1 ≤ n ≤ 10^7。
耗时限制1000ms 内存限制256MB
解析
考点:进制转换
本质上来说,本题是进制转换, 但不允许拆分出来的 2 进制的最低位为 1。由于 2 进制 的最低位为 1,得到的 10 进制是奇数,因此奇数不可能有符合条件的拆分。
举例能拆分的正偶数,比如: 10,拆分 2 进制后是 1010,那么这个拆分其实是值为 1 的 这些 2 进制位对应的十进制,也就是:8 2。
参考代码:
#include <bits/stdc++.h>
using namespace std;
/*
定义:分解为了若干个不同的 2 的正整数次幂
性质:是偶数,奇数不存在优秀的拆分
思路:
如果 n 是偶数,将 n 进行进制转换
10 -> 1010
*/
int a[110],n,k = 0;//k 表示 a 数组的下标
int main(){
cin>>n;
//特判奇数的情况
if(n % 2 != 0){
cout<<-1;
return 0;
}
//进制转换
int t = 1;//表示 2 的次方
while(n != 0){
if(n % 2 != 0){
k++;
a[k] = t;
}
t = t * 2;
n = n / 2;
}
//逆序输出结果
for(int i = k;i >= 1;i--){
cout<<a[i]<<" ";
}
return 0;
}2020年CSP-J-T2-直播获奖(live)
题目描述
NOI2130 即将举行。为了增加观赏性,CCF决定逐一评出每个选手的成绩,并直播即时的获奖分数线。本次竞赛的获奖率为w%,即当前排名前w%的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了p个选手的成绩,则当前计划获奖人数为max(1, [p * w%]),其中w是获奖百分比,[x]表示对x向下取整,max(x, y) 表示x和y中较大的数。
如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮CCF写一个直播程序。
输入格式
输入文件名为live.in。
第1行两个正整数n, w。分别代表选手总数与获奖率。
第2行有n个非负整数,依次代表逐一评出的选手成绩。
输出格式
输出文件名为 live.out。
只有一行,包含n个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
输入输出样例
输入样例1:
10 60 200 300 400 500 600 600 0 300 200 100
输出样例1:
200 300 400 400 400 500 400 400 300 300
输入样例2:
10 30 100 100 600 100 100 100 100 100 100 100
输出样例2:
100 100 600 600 600 600 100 100 100 100
说明
【样例 1 解释】
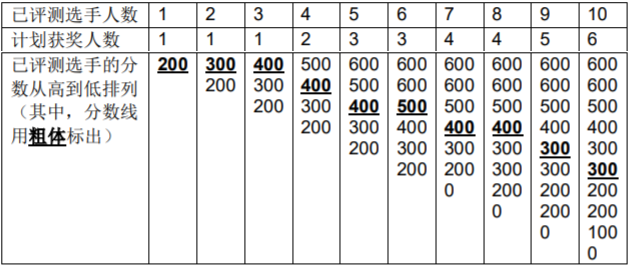
注意,在第9名选手的成绩评出之后,计划获奖人数为5人,但由于有并列,因此实际会有6人获奖。
【数据范围与提示】
测试点编号n
第1~3测试点:n=10
第4~6测试点:n=500
第7~10测试点:n=2000
第11~17测试点:n=10000
第18~20测试点:n=100000
对于所有测试点,每个选手的成绩均为不超过600的非负整数,获奖百分比w是一个正整数且 1 ≤ w ≤ 99。
在计算计划获奖人数时,如用浮点类型的变量(如 C/C++中的 float、double,Pascal 中的 real、double、extended 等)存储获奖比例 w%,则计算 5 × 60% 时的结果可能为 3.000001,也可能为 2.999999,向下取整后的结果不确定。
因此,建议仅使用整型变量,以计算出准确值。
耗时限制1000ms 内存限制256MB
解析
考点:数组标记,优先队列
解法一:数组标记,时间复杂度(保留了常数):O(600×n)
本题是求, 在有 i 人的情况下, 前 w%人的最低分数线是多少。
本题要注意,数据比较多,因此要注意防止超时:
1. 用 scanf 和 printf 提升读写效率(也可以快读快写)
2. 用数组计数法,统计有 i 个人的情况下,每个分数有多少人(本题分数最多是 600), 从大到小数出前 w%人, 就知道分数线是多少了。
参考代码
#include <bits/stdc++.h>
using namespace std;
/*
1.获奖人数为 k = max(1, int(p × w%))
2.选手的成绩均为不超过 600 的非负整数
思路:使用数组统计每个分值得分的人数
从大到小统计出 k 个人,最后一次循环对应的分值就是要求的获奖分数
*/
int a[610];
int n,w,x;
int main(){
scanf("%d%d",&n,&w);
int k;//获奖人数
int ans;//统计人数
//读入 n 个人的分数,读一个算一个
for(int i = 1;i <= n;i++){
scanf("%d",&x);
a[x]++;//统计每个分值对应的人数
//计算获奖人数
k = max(1,int(i * w / 100.0));
ans = 0;
//从最高分的人数向下统计出>=k 个人
for(int j = 600;j >= 0;j--){
if(ans + a[j] < k) ans += a[j];//+=
else{
printf("%d ",j);
break;
}
}
}
return 0;
}解法二:优先队列
如果分数大小没有限制, 那么类似动态中位数的题目,可以采用对顶堆写法,时间复杂度 O(nlogn):
#include <bits/stdc++.h>
using namespace std;
//已经获奖,小根堆
priority_queue<int, vector<int>, greater<int> > q1;
//候选获奖,大根堆
priority_queue<int> q2;
int main(){
int n, w, num;
cin >> n >> w;
for(int i = 1; i <= n; i++) {
cin >> num;//分数
int cnt = max(1, i * w / 100);//计划获奖人数
//1.放到候选堆
q2.push(num);
//2.判断是否需要放到获奖堆里
//3. 如果需要多放,直接把q2的堆顶元素放到q1
while(cnt > q1.size() && !q2.empty() ) {
q1.push(q2.top());
q2.pop();
}
//4. 放完之后,还要要判断当前q2的堆顶是否比q1的堆顶大
while(!q1.empty() && !q2.empty() && q1.top() < q2.top()){
int t = q1.top();
q1.pop();
q1.push(q2.top());
q2.push(t);
q2.pop();
}
//5. 输出获奖分数线
cout << q1.top() << " ";
}
}
2020年CSP-J-T3-表达式(expr)
题目描述
小C热衷于学习数理逻辑。有一天,他发现了一种特别的逻辑表达式。在这种逻辑表达式中,所有操作数都是变量,且它们的取值只能为 0 或 1,运算从左往右进行。如果表达式中有括号,则先计算括号内的子表达式的值。特别的,这种表达式有且仅有以下几种运算:
1. 与运算:a & b。当且仅当a和b的值都为1时,该表达式的值为1。其余情况该表达式的值为0。
2. 或运算:a | b。当且仅当a和b的值都为0时,该表达式的值为0。其余情况该表达式的值为1。
3. 取反运算:!a。当且仅当a的值为0时,该表达式的值为1。其余情况该表达式的值为0。
小C想知道,给定一个逻辑表达式和其中每一个操作数的初始取值后,再取反某一个操作数的值时,原表达式的值为多少。
为了化简对表达式的处理,我们有如下约定:
表达式将采用后缀表达式的方式输入。后缀表达式的定义如下:
1. 如果 E 是一个操作数,则 E 的后缀表达式是它本身。
2. 如果 E 是 E1 op E2 形式的表达式,其中 op 是任何二元操作符,且优先级不高于E1、E2中括号外的操作符,则 E 的后缀式为 E1′E2′op,其中 E1′、E2′ 分别为 E1、E2 的后缀式。
3. 如果 E 是 (E1) 形式的表达式,则 E1 的后缀式就是 E 的后缀式。
同时为了方便,输入中:
a) 与运算符(&)、或运算符(|)、取反运算符(!)的左右均有一个空格,但表达式末尾没有空格。
b) 操作数由小写字母 x 与一个正整数拼接而成,正整数表示这个变量的下标。例如:x10,表示下标为 10 的变量 x10。数据保证每个变量在表达式中出现恰好一次。
输入格式
输入文件名为 expr.in。
第一行包含一个字符串 s,表示上文描述的表达式。
第二行包含一个正整数 n,表示表达式中变量的数量。表达式中变量的下
标为 1,2, … , n。
第三行包含 n 个整数,第 i 个整数表示变量 Xi 的初值。
第四行包含一个正整数 q,表示询问的个数。
接下来 q 行,每行一个正整数,表示需要取反的变量的下标。注意,每一个询问的修改都是临时的,即之前询问中的修改不会对后续的询问造成影响。
数据保证输入的表达式合法。变量的初值为 0 或 1。
输出格式
输出文件名为 expr.out。
输出一共有 q 行,每行一个 0 或 1,表示该询问下表达式的值。
输入输出样例
输入样例1:
x1 x2 & x3 | 3 1 0 1 3 1 2 3
输出样例1:
1 1 0
输入样例2:
x1 ! x2 x4 | x3 x5 ! & & ! & 5 0 1 0 1 1 3 1 3 5
输出样例2:
0 1 1
说明
【样例 1 解释】
该后缀表达式的中缀表达式形式为 (x1 & x2) | x3。
对于第一次询问,将 x1 的值取反。此时,三个操作数对应的赋值依次为0,0,1。原表达式的值为(0 & 0)|1 = 1。
对于第二次询问,将 x2 的值取反。此时,三个操作数对应的赋值依次为1,1,1。原表达式的值为(1 & 1)|1 = 1。
对于第三次询问,将 x3 的值取反。此时,三个操作数对应的赋值依次为1,0,0。原表达式的值为(1 & 0)|0 = 0。
【样例 2 解释】
该表达式的中缀表达式形式为 ( ! x1) & (! (( x2|x4) & ( x3 & (! x5) )))。
【数据范围与提示】
对于 20% 的数据,表达式中有且仅有与运算(&)或者或运算(|)。
对于另外 30% 的数据,|s| ≤ 1000,q ≤ 1000,n ≤ 1000。
对于另外 20% 的数据,变量的初值全为 0 或全为 1。
对于 100% 的数据,1 ≤ |s| ≤ 1 × 10^6,1 ≤ q ≤ 1 × 10^5,2 ≤ n ≤ 1 × 10^5。
其中,|s| 表示字符串 s 的长度。
耗时限制1000ms 内存限制256MB
解析
考点:二叉树、深搜、栈、后缀表达式
分析:
首先输入的一行字符串要先解析,利用栈来建表达式树,这就是一个小模拟。
对于非运算,直接用德·摩根定律,下传标记让子树信息都反一下,这样写方便后续处理。
德·摩根定律:
- !(P & Q) = (! P) | (! Q)
- !(P | Q) = (! P) & (! Q)
题目里有个关键信息是“每个变量在表达式中出现恰好一次”,而每个询问只改变一个变量的值,为什么要有这么一个限制条件?(当然,肯定有用啦)
这对原答案来说就产生两个可能:变或不变。这听起来是一句废话,其实蕴含的意思是: 有些变量对整个表达式起决定作用,其改变则原答案也改变;有些变量对整个表达式根本没用,其变不变原答案都不变。
说明白一点,就是:
1 & x = x,0 | x= x里的 x 就起了决定性作用,改变了 x,最终答案就改变0 & x = 0,1 | x= 1的 x 就是一个无用变量,改变了 x,最终答案不变
那我们就给树上每个结点建一个标记,对 & 来说,如果一棵子树是 0,那另外一棵子树内所有叶结点都应该打上废物标记,对|同理。
先计算出原表示答案ans,这样我们在查询的时候,没被标记的就说明它往上到根节点都不存在一种让它变成无用的运算,所以答案是!ans,如果有标记则答案依旧为ans。
时间复杂度O(n+q)。
参考代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
char s[N];
int a[N], lson[N], rson[N], ck; // 树, a[1]~a[n] 叶子节点(x?) a[n+1]~a[ck] 运算符(2:&, 3:|)
bool flag[N], c[N]; // flag[i]=1: !取反符号 c[i]=1: 改变 x_i 的值对结果无影响
int n, q;
stack<int> stk;
int dfs(int root, int f){
a[root] ^= f; // 德摩根定律,取反后,运算符改变 &->|, |->&
if(root <= n)
return a[root];
// 计算左右表达式的值
int x = dfs(lson[root], f ^ flag[lson[root]]);
int y = dfs(rson[root], f ^ flag[rson[root]]);
if(a[root] == 2) {
if(x == 0) c[rson[root]] = 1; // x=0, 改变 y 所在表达式对结果无影响
if(y == 0) c[lson[root]] = 1; // y=0, 改变 x 所在表达式对结果无影响
return x & y;
} else {
if(x == 1) c[rson[root]] = 1; // x=1, 改变 y 所在表达式对结果无影响
if(y == 1) c[lson[root]] = 1; // y=1, 改变 x 所在表达式对结果无影响
return x | y;
}
}
// 向下传递"修改无用"标记:修改 x 无用,那么修改 x 下面的子树肯定也无用
void dfs2(int root){
if(root <= n) return;
c[lson[root]] |= c[root];
c[rson[root]] |= c[root];
dfs2(lson[root]);
dfs2(rson[root]);
}
int main(){
fgets(s, N, stdin);
cin >> n;
ck = n;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 0; s[i]; i += 2){
if(s[i] == 'x'){
int x = 0;
i++;
while(s[i] != ' ')
x = x * 10 + s[i++] - '0';
i--;
stk.push(x);
} else if(s[i] == '&') {
int x = stk.top();
stk.pop();
int y = stk.top();
stk.pop();
stk.push(++ck); // 压入运算符
a[ck] = 2; // 2 ^ 1 = 3
lson[ck] = x;
rson[ck] = y;
} else if(s[i] == '|') {
int x = stk.top();
stk.pop();
int y = stk.top();
stk.pop();
stk.push(++ck); // 压入运算符
a[ck] = 3; // 3 ^ 1 = 2
lson[ck] = x;
rson[ck] = y;
} else if(s[i] == '!') {
flag[stk.top()] ^= 1; // 考虑到可能有连续取反,因此这里不能直接赋值为 1
}
}
int ans = dfs(ck, flag[ck]);
dfs2(ck);
cin >> q;
while(q--) {
int x;
cin >> x;
cout << (c[x] ? ans : ! ans) << '\n';
}
return 0;
}
补充画图说明解法二
本题要点:
1.后缀表达式对应于一棵表达式树
2.由于数据量的限制,不能每次都将整个表达式的树都计算一遍
3.优化点: 从上向下深搜,记录哪些点的值变化会导致结果的变化
思路:
1.求表达式的值
2.深搜求哪些点的值可能会影响表达式的值
3.q 次询问,每次判断当前结点的修改是否影响表达式的值



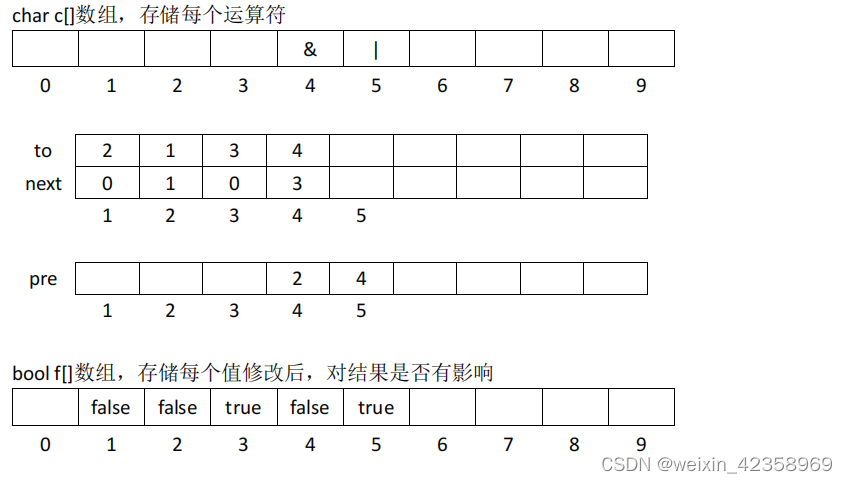
参考代码:
#include <bits/stdc++.h>
using namespace std;
/*
取反某一个操作数的值时,原表达式的值为多少
思路:
1.读入表达式,将表达式建成二叉树
2.计算出表达式的值
3.深搜,求出哪些结点的值修改后对结果有影响
*/
const int N = 1e6 + 10;
struct node{
int to,next;
}a[N];//邻接表
int pre[N],k;//存储以每个点为起点的最后一条边的编号
int num[N];//存储二叉树每个结点的值
char c[N];//存储操作符
int m;//表示 c 数组的下标
bool f[N];//标记哪些点的值修改后对结果有影响
int n;
string s,w;//w 用来存储每个操作数的下标
stack<int> st;//用于计算后缀表达式
//建边
void add(int u,int v){
k++;
a[k].to = v;
a[k].next = pre[u];
pre[u] = k;
}
//深搜求哪些结点的值修改后对结果有影响
void dfs(int x){
f[x] = true;
if(x <= n) return;//如果是叶子结点
if(c[x] == '!') dfs(a[pre[x]].to);
else{
int n1 = a[pre[x]].to,n2 = a[a[pre[x]].next].to;
if(c[x] == '&'){
if(num[n1] == 1) dfs(n2);
if(num[n2] == 1) dfs(n1);
}else if(c[x] == '|'){
if(num[n1] == 0) dfs(n2);
if(num[n2] == 0) dfs(n1);
}
}
}
int main(){
getline(cin,s);
cin>>n;
for(int i = 1;i <= n;i++){
scanf("%d",&num[i]);
}
//分析表达式,建树
int x,y;
m = n;
for(int i = 0;i < s.size();i++){
if(isdigit(s[i])){
w = w + s[i];
//如果连续数字结束
if(i==s.size()-1||!isdigit(s[i+1])){
st.push(atoi(w.c_str()));//将操作数的下标入栈
w = "";
}
}else if(s[i] == '!'){
//如果是取反操作符
m++;
c[m] = s[i];//操作符的编号是 m
x = st.top();//取栈顶元素来运算
st.pop(); //出栈
//建边
add(m,x);
num[m] = !num[x];
st.push(m);
}else if(s[i] == '&' || s[i] == '|'){
//如果是& |操作符
m++;
c[m] = s[i];
//取 2 个操作数
x = st.top();
st.pop();
y = st.top();
st.pop();
//建边
add(m,x);
add(m,y);
//计算结点的值
if(s[i] == '&') num[m] = num[x] & num[y];
else if(s[i] == '|') num[m] = num[x] | num[y];
st.push(m);
}
}
int ans = num[st.top()];
//cout<<ans;
//深搜求哪些结点的值修改后对结果有影响
dfs(st.top());//从根开始深搜
//q 次询问
int q;
cin>>q;
while(q--){
scanf("%d",&x);
if(f[x]==true) printf("%d\n",!ans);
else printf("%d\n",ans);
}
return 0;
}2020年CSP-J-T4-方格取数(number)
题目描述
设有n×m的方格图,每个方格中都有一个整数。现有一只小熊,想从图的左上角走到右下角,每一步只能向上、向下或向右走一格,并且不能重复经过已经走过的方格,也不能走出边界。
小熊会取走所有经过的方格中的整数,求它能取到的整数之和的最大值。
输入格式
输入文件名为 number.in。
第1行两个正整数 n, m。
接下来n行每行m个整数,依次代表每个方格中的整数。
输出格式
输入文件名为 number.out。
一个整数,表示小熊能取到的整数之和的最大值。
输入输出样例
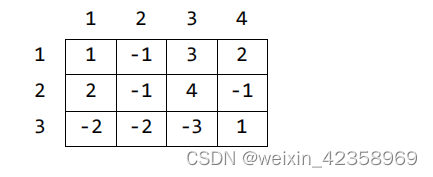
输入样例1:
3 4 1 -1 3 2 2 -1 4 -1 -2 2 -3 -1
输出样例1:
9
输入样例2:
2 5 -1 -1 -3 -2 -7 -2 -1 -4 -1 -2
输出样例2:
-10
说明
【样例1解释】
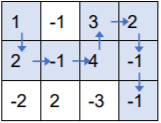
按上述走法,取到的数之和为 1 + 2 + (-1) + 4 + 3 + 2 + (-1) + (-1) = 9,可以证明为最大值。
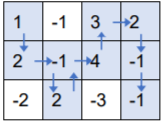
注意,上述走法是错误的,因为第2行第2列的方格走过了两次,而根据题意,不能重复经过已经走过的方格。
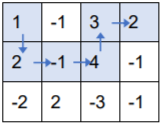
另外,上述走法也是错误的,因为没有走到右下角的终点。
【样例2解释】
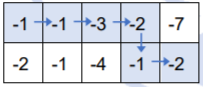
按上述走法,取到的数之和为(-1) + (-1) + (-3) + (-2) + (-1) + (-2) = -10,可以证明为最大值。因此,请注意,取到的数之和的最大值也可能是负数。
【数据范围与提示】
对于 20% 的数据,n, m ≤ 5。
对于 40% 的数据,n, m ≤ 50。
对于 70% 的数据,n, m ≤ 300。
对于 100% 的数据,1 ≤ n, m ≤ 1000。方格中整数的绝对值不超过 10^4。
耗时限制1000ms 内存限制256MB
解析:
考点:坐标DP,深搜,广搜,记忆化搜索
解法一、按层(列)广搜优先队列写法:70分左右
#include <bits/stdc++.h>
using namespace std;
int n,m;
long long f[1010],f2[1010],s[1010];
vector<long long> a[1005];
priority_queue<long long> q;
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++) {
a[i].push_back(0);
for(int j=1;j<=m;j++) {
int t;
cin>>t;
a[i].push_back(t);
}
}
for(int i=1;i<=n;i++) {
f[i]=f[i-1]+a[i][1];
}
for(int j=2;j<=m;j++) {
for(int i=1;i<=n;i++) {
s[i]=s[i-1]+a[i][j];
f2[i]=-100000000000;
}
for(int i=1;i<=n;i++) {
q.push(f[i]+s[n]-s[i-1]);
long long p=q.top();
f2[i]=max(f2[i],p+s[i]-s[n]);
}
while(!q.empty()) q.pop();
for(int i=n;i>=1;i--) {
q.push(f[i]+s[i]);
long long p=q.top();
f2[i]=max(f2[i],p-s[i-1]);
}
for(int i=1;i<=n;i++) {
f[i]=f2[i];
}
while(!q.empty()) q.pop();
}
cout<<f[n]<<"\n";
return 0;
}
解法二、记忆化搜索,满分
采用自上而下的记忆化搜索,设fi,j,0 表示从一个格子上方走到该格子的路径最大和,fi,j,1 表示从一个格子下方走到该格子的路径最大和。如果搜到以前搜过的状态则直接返回搜过的最大和(也就是 f 中的值),否则继续搜索到达该格时的最大和。
时间复杂度:O(nm)
#include<bits/stdc++.h>
using namespace std;
long long n,m,a[1005][1005];
long long f[1005][1005][3];
// 0: shang 1: xia 2 you
long long dfs(int x,int y,int dir){
if(x<1||x>n||y<1||y>m) return -0x3f3f3f3f;
if(x==n&&y==m){
return a[n][m];
}
if(f[x][y][dir]) return f[x][y][dir];
if(dir==0) return f[x][y][dir]=max(dfs(x-1,y,0), dfs(x-1,y,2))+a[x][y];
if(dir==1) return f[x][y][dir]=max(dfs(x+1,y,1), dfs(x+1,y,2))+a[x][y];
if(dir==2) return f[x][y][dir]=max(dfs(x,y+1,1),max(dfs(x,y+1,0), dfs(x,y+1,2)))+a[x][y];
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
cout << max(dfs(1,1,2), dfs(1,1,1));
return 0;
}
解法三:普通 DP
不同于其他题只能走上右或下右,该题能走上下右。
首先,我们思考,只能走右不能走左,意味着我们可以单独将每一列分开求解,而向右走其实是从某列运动到下一列,下一列再运动到下下一列……实质上是一个递推的过程。
然后对于每一列,因为不能重复经过已经走过的方格,所以要么只能往上走,要么只能往下走。
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, m, a[N][N];
long long dp[N][N], up[N], dw[N];
/*
对于每一个位置:上一步有三种行走可能
dp[i][j] = max{dp[i][j-1], dw[i][j-1], up[i][j+1]} + a[i][j];
*/
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> a[i][j];
for(int i = 1; i <= n; i++)
dp[i][1] = dp[i-1][1] + a[i][1];
for(int j = 2; j <= m; j++){
// 从上往下
dw[1] = dp[1][j-1] + a[1][j];
for(int i = 2; i <= n; i++)
dw[i] = max(dp[i][j-1], dw[i-1]) + a[i][j];
// 从下往上
up[n] = dp[n][j-1] + a[n][j];
for(int i = n-1; i >= 1; i--)
up[i] = max(dp[i][j-1], up[i+1]) + a[i][j];
// dp:从左侧过来已经包含到上面两种情况中,所以可以不写
for(int i = 1; i <= n; i++)
dp[i][j] = max(dw[i], up[i]);
}
cout << dp[n][m] << endl;
return 0;
}
简单一些的写法:
#include <bits/stdc++.h>
using namespace std;
/*
左上角走到右下角
每一步只能向上、向下或向右走一格
不能重复经过已经走过的方格
计算的结果,要用 long long
*/
const int N = 1010;
int a[N][N];//读入的每个点的值
typedef long long LL;
LL f[N][N];
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
scanf("%d",&a[i][j]);
}
}
/*
DP 求出走到每个点经过的数字和的最大值
一列一列求,对于每一列而言,要求从上向下走到每个点经过的数字和的最大值
也要求从下向上走到每个点经过的数字和的最大值
*/
memset(f,-0x7f,sizeof(f));
LL ma;//走到每个格子经过的数字和最大
f[1][0] = 0;
for(int j = 1;j <= m;j++){
//从上向下求
ma = -1e18;
for(int i = 1;i <= n;i++){
ma = max(ma,f[i][j-1]) + a[i][j];
f[i][j] = max(f[i][j],ma);
}
//从下向上求
ma = -1e18;
for(int i = n;i >= 1;i--){
ma = max(ma,f[i][j-1]) + a[i][j];
f[i][j] = max(f[i][j],ma);
}
}
cout<<f[n][m];
return 0;
}dp(f) 数组降维写法:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int n, m, a[N][N];
long long f[N], up[N], down[N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
for(int i = 1; i <= n; i++)
f[i] = f[i-1] + a[i][1];
for(int j = 2; j <= m; j++) {
up[1] = f[1] + a[1][j];
for(int i = 2; i <= n; i++)
up[i] = max(f[i], up[i-1]) + a[i][j];
down[n] = f[n] + a[n][j];
for(int i = n-1; i >= 1; i--)
down[i] = max(f[i], down[i+1]) + a[i][j];
for(int i = 1; i <= n; i++)
f[i] = max(up[i], down[i]);
}
cout << f[n];
return 0;
}






















 3072
3072











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








