OI退役笔记-003：数论（三）约数（GCD、LCM、EXGCD）

一、约数

约数，又称因数。整数 a 除以整数 b (b ≠ 0) 除得的商正好是整数而没有余数，我们就说 a 能被 b 整除，或 b 能整除 a。a 称为 b 的倍数，b 称为 a 的约数。
唯一分解定理
唯一分解定理一般指算术基本定理，可表述为：对于任一大于 1 的自然数 N，如果 N 不是质数，那么 N 可以唯一分解成有限个质数的乘积，即：

N = P₁^(a1) * P₂^(a2) * … * P_n^(an)

其中 P₁，P₂，…，P_n 表示质数（Prime）。

应用

对于一个大于 1 的正整数N，如果它可写成N = P₁^(a1) * P₂^(a2) * … * P_n^(an) 的形式，则：

它的正因数个数为：

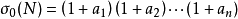
它的全体正因数之和为：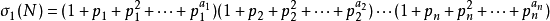
举例说明白：
180 = 2² * 3² * 5¹
个数 = (1 + 2) * (1 + 2) * (1 + 1) = 18
总和 = (1 + 2 + 4) * (1 + 3 + 9) * (1 + 5) = 546

其他的小性质：

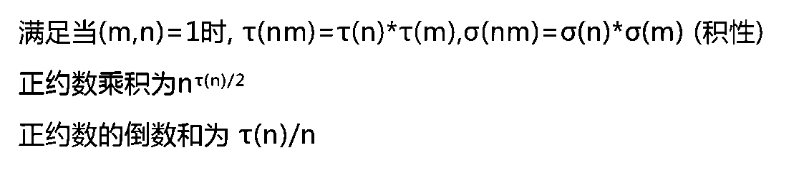
求 N 的正整数集合

求 1 ~ N 的正整数集合

二、最大公约数

gcd(a, b)：a 与 b 的最大公约数，就是 a, b 这两个正整数的最大公共因子；
lcm(a, b)：a 与 b 的最小公倍数，就是 a, b 这两个正整数的最小公共倍数。

且有定理：∀ a, b ∈ N，gcd(a, b) * lcm(a, b) = a * b，因此有：

lcm(a, b) = (a * b) / gcd(a, b)

而求 gcd(a, b) 的两种主要方法是 辗转相除法 和 辗转相减法 。

（以下不妨设b ≤ a）
辗转相减法：gcd(a, b) = gcd(b, a − b)
辗转相除法：gcd(a, b) = gcd(b, a % b)

其中，前者的复杂度是 O(n)，后者的复杂度是 O(logn)。其中 n = max(a, b)

辗转相除法的证明：

看看就好 来源：百度百科

gcd(a, b) 的实现：

实现：

// 辗转相减
int gcd(int a, int b)
{
    if (a == b)
        return a;
    else if (a > b)
        return gcd(b, a - b);
    else
        return gcd(a, b - a);
}

// 辗转相除
int gcd(int x, int y) {
	if (y == 0)
		return x ;
		
	return gcd(y, x % y);
}

辗转相减法的优化：

需加语句、头文件：

#define min(a, b)	(((a) < (b)) ? (a) : (b))

实现：

int qgcd(int a, int b) {
	
	if (a == 0)
		return b;
	if (b == 0)
		return a;
	if (!(a & 1) && !(b & 1))
		return qgcd(a >> 1, b >> 1) << 1 ;
	else if (!(b & 1))
		return qgcd(a, b >> 1) ;
	else if (!(a & 1))
		return qgcd(a >> 1, b) ;
	else
		return qgcd(abs(a - b), min(a, b)) ;
}

解释：
当 a, b 均是偶数时，显然 gcd(a, b) 有一因数 2。因此 gcd(a, b) = 2 × gcd(a / 2, b / 2)

当 a, b 一奇一偶的时候，不妨设 a 是偶数。显然 gcd(a, b) 不含因子 2。于是有 gcd(a, b) = gcd(a / 2, b)

当 a, b 同为奇数时，直接应用辗转相减法。gcd(a, b) = gcd(b, a − b)。

三、例题

约数比较模糊，也有许多推理，因此想放几道例题，但由于精力有限，先放一道例题及分析。

解这道题需要三个引理：
引理 1：1 ~ N 中最大的反质数就是1 ~ N 中约数最多的数中最小的一个。
证明：设 M 是该数，则对于 ∀ x < M，有 g(x) < g(M)；对于 ∀ M < x ≤ N，有 g(M) ≤ g(x)。

引理 2：对于本题（或大部分题），1 ~ N 中任何数的不同质因子不会超过 10 个，且所有质因子指数综合不超过 30。
扯皮 证明：最小的十个质数的乘积 > 10⁹，且 2³⁰ > 10⁹，因此在这道题中，该引理可用。

引理 3：x 为反质数的必要条件：从 2 ~ 29 这 10 个 质数都能整除 x，且分解质因数后从 2 到 29 的指数不增。
证明同 2。

确定算法：深搜

四、扩展 gcd [exgcd(a, b)]：

斐蜀定理：
对任何整数 a, b 和它们的最大公约数 gcd(a, b)，关于未知数 x 和 y 的线性方程（称为裴蜀等式）：ax + by = c
当且仅当 c 是 gcd(a, b) 的倍数时有整数解。裴蜀等式有解时必然有无穷多个解。

扩展 gcd
求解关于 x, y 的方程 ax + by = c（a, b, c ∈ Z）的整数解可以用扩展 gcd。证明裴蜀定理采用数学归纳法，证明的过程就是扩展 gcd 的特解的求解的过程。

扩展 gcd 实现：
区分概念：所要求的解是 ax + by = c，而只有 c % gcd(a, b) == 0，时有解，所以我们实际求的是 ax + by = gcd(a, b)。最后 x、y 分别乘以 c / gcd(a, b) 即可。后续会详细讲解。

int exgcd(int a, int b, int &x, int &y)
{
	// a * x + 0 * y = c (c = a)
	// x = c / a
    if (b == 0)
    {
        x = 1;
		y = 0;
		return a;
    }
    
    // gcd() 的框架
	int r = exgcd(b, a % b, x, y);
	int k = x;
	// 公式
	x = y;
	y = k - a / b * y;
	
    return r;
}

上一深度的 x 等于下一深度的y₁，上一深度的 y 等于下一深度的x₁ - (a / b) * y₁。 也就实现了 x, y 的值向上一层传递的问题，进而求出原等式的一组解。 需要注意，上面推导时用的除法都是整型除法。

由特殊解到一般解：

根据裴蜀定理求 ax + by = c 的一般解：
我们知道裴蜀定理的前提就是：a, b ∈ Z，且 c 是 gcd(a, b) 的倍数。

那么一定有：c % gcd(a, b) == 0，保证该方程存在整数解，否则不存在整数解。

我们知道 ax + by = gcd(a, b) 的特解 (x₀, y₀) 来说：
a * x₀ * (c / gcd(a, b)) + b * y₀ * (c / gcd(a, b) = gcd(a, b) * (c / gcd(a, b)) = c。
令等式ax + by = c 的特解为 (x₁, y₁)，
那么 x₁ = x₀ * (c / gcd(a, b)); y1 = y₀ * (c / gcd(a, b));
把求出的 (x₀, y₀) 都乘以 c /gcd(a, b) 就是方程 ax + by = c 的特解。

再次探讨斐蜀定理

图小见谅！

作者：Rotch
日期：2020-09-30
修改：2020-05-12
[2020-05-12]：重新调整知识结构
[2020-05-13]：重写对扩展 gcd 的讲解
[2020-05-14]：删除部分超纲内容