动态演示：B树的生长与平衡过程

本文还有配套的精品资源，点击获取

简介：B树是一种平衡多路查找树，广泛应用于数据库和文件系统中，以实现高效的数据排序和操作。本资源通过Flash动画展示B树如何动态调整结构来应对数据的插入和删除。该演示详细解释了B树的构造、插入和删除操作、查找过程、树高影响以及其平衡性质，帮助学习者通过视觉体验深入理解B树的工作原理。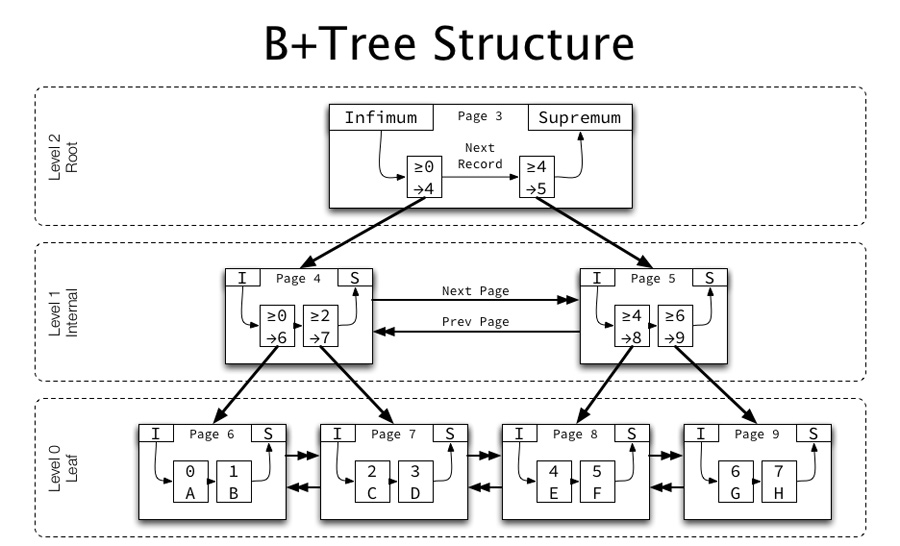

1. B树的定义与应用场景

B树是一种自平衡的树数据结构，它维护数据的排序，并允许搜索、顺序访问、插入和删除在对数时间内完成。它被设计用来有效地处理数据存储系统中的大量数据，尤其是在磁盘或其他直接访问存储设备上。由于其平衡性和多路特性，B树能够最大限度地减少磁盘I/O操作次数，因此在数据库系统和文件系统领域中广泛应用。

在数据库系统中，B树用于索引结构，加速查询操作。而在文件系统中，B树用于管理文件元数据，如索引节点（inode）。该结构的特性特别适合用于实现大型文件的存储和检索，尤其是在数据量大、读写频繁的场景下。此外，B树也用于实现数据库的事务日志记录和恢复机制。

随着数据量的不断增长，B树及其变体如B+树和B*树，成为解决大规模数据组织和检索问题的关键技术。在下一章中，我们将深入探讨B树节点的结构细节，以此来理解其高效性的根本所在。

2. B树节点结构深入剖析

在讨论数据结构时，节点是构成树形结构的基础单元。B树作为重要的索引数据结构，其节点结构设计对于维护树的平衡性和提高操作效率起着关键作用。本章将深入分析B树节点的基本组成，以及节点之间的组织形式。

2.1 B树节点的基本组成

2.1.1 节点的度和关键字数量

在B树中，一个节点的度定义为其子节点的数量上限。B树的度是固定的，即每个节点能拥有的最大子节点数。度的大小直接影响B树的高度和性能，因此通常会根据应用的特点预设一个合适的值。例如，在一个B树中，如果其度为 t ，那么这个B树被称为 t 阶B树。

节点包含的关键字数量（记为 n ）与子节点数量（记为 n+1 ）直接相关。每个非根节点都包含最少 [t/2]-1 个关键字，但不超过 t-1 个关键字，这样可以保证节点的充分利用，同时维护树的平衡。根节点作为特例，可以少于 [t/2]-1 个关键字，甚至在B树只有根节点一个节点时，根节点可以为空。

2.1.2 节点中的数据和指针

每个B树节点通常由三部分组成：节点的索引指针、数据项以及指向子节点的指针。节点中会存储一系列有序的关键字（数据项），这些关键字用于表示子节点中存储的数据范围。

索引指针指向子节点，用于快速定位数据。在数据项之间以及数据项与指针之间，B树维护了有序性，这意味着所有指向子节点的指针都按照关键字的值有序排列。当数据项数量变化时，指针的增加或删除也会对应地反映在子节点的索引中。

2.2 B树节点的组织形式

2.2.1 索引顺序和平衡条件

B树的平衡性是其能够高效进行查找和插入操作的关键。平衡条件要求所有叶子节点都位于同一层级，从根节点到任何一个叶子节点的所有路径的长度相同。为保持这种平衡，B树的节点组织必须遵循严格的规则。

每个节点中的关键字将节点的索引区域分为多个子区间，每个子区间都对应一个子节点。例如，假设有关键字 k1, k2, ..., kn ，那么第一个关键字 k1 之前的数据项会在第一个子节点中查找，第二个关键字 k2 与 k1 之间的数据项在第二个子节点中查找，依此类推，直到最后一个子节点。

2.2.2 子节点指针与数据项的关系

为了保持树的平衡性，子节点指针的数量总是比关键字的数量多一个。索引指针的数量将决定节点能分割成多少个区间，而关键字数量则实际定义了这些区间的分界。

在实现B树节点时，通常会有一个数组来存储指针，与之对应的，关键字也会存储在另一个数组中。通过指针数组的索引和关键字数组中的值，可以确定数据项所在的子区间，并据此进行数据的查找和节点的分裂或合并操作。

这些内容为第二章的核心部分，为理解B树节点的深入细节提供了坚实的基础。接下来的内容将转向B树的动态操作流程，揭示如何通过节点分裂和合并来维护树的平衡性。

3. B树的动态操作流程

B树在数据管理中经常执行动态操作，包括数据的插入和删除。这些操作会改变树的结构，有时需要分裂节点，有时需要合并节点，以保持B树的关键特性。本章将详细探讨这些操作流程，帮助读者更深入地理解B树的动态行为。

3.1 动态数据插入与节点分裂机制

在B树中插入数据是一个复杂的过程，需要考虑多个方面来保证树的平衡性。当插入数据导致节点超出其容量时，节点就会分裂。下面我们详细探讨这一过程。

3.1.1 插入数据时的节点处理流程

在进行数据插入操作时，首先需要定位到叶子节点。B树插入数据的基本步骤如下：

1. 从根节点开始，根据待插入数据的值与节点中的关键字比较，选择适当的子节点。
2. 如果当前节点是一个叶子节点，直接将数据插入该节点；如果不是，进入步骤1递归搜索。
3. 如果节点中的关键字数量没有达到最大容量（2t-1个关键字，t为树的最小度），则直接插入；否则需要执行节点分裂。

3.1.2 节点分裂的触发条件和操作

节点分裂是保证B树平衡的关键步骤，其触发条件是节点的关键字数量达到或超过最大容量。具体操作如下：

1. 从节点的中间关键字开始，将节点拆分为两个节点，每个节点包含t-1个关键字。
2. 将中间关键字上移至父节点，作为分隔两个新节点的界限。
3. 如果父节点也因分裂而超过容量，则需要递归执行父节点的分裂操作。

下面是一个节点分裂的简单示例代码：

def split_node(node):
    t = node.t  # 最小度数
    new_node = Node(t)
    middle_key_index = t - 1
    new_node.keys = node.keys[middle_key_index + 1:]  # 新节点包含的键值
    node.keys = node.keys[:middle_key_index]  # 原节点包含的键值
    return new_node

class Node:
    def __init__(self, t):
        self.t = t  # 最小度数
        self.keys = []  # 关键字列表
        self.children = []  # 子节点列表
        self.is_leaf = True  # 是否为叶子节点

    def __str__(self):
        return f"Node: {self.keys}, Children: {len(self.children)}"

在这个代码中，我们定义了一个 Node 类来代表B树的节点，并提供了一个 split_node 函数用于处理节点分裂。为了简化，这里没有包括父节点的处理逻辑和递归分裂调用。

3.2 数据删除操作及节点合并策略

数据删除操作可能需要调整树的结构，甚至需要合并节点以保持树的平衡性。节点合并的触发条件是当节点的关键字数量低于最小值（t-1个关键字）时。

3.2.1 删除数据时的节点处理流程

删除操作相对复杂，可能涉及到多种情况。基本流程如下：

1. 从根节点开始，根据待删除数据的值与节点中的关键字比较，确定搜索路径。
2. 如果关键字存在于叶子节点，直接删除；如果存在于非叶子节点，需要找到前驱或后继节点替换删除的关键字，再删除。
3. 如果节点的关键字数量不低于最小值，则直接删除；如果低于最小值，则需要执行节点合并或借用操作。

3.2.2 节点合并的条件和操作

节点合并是在删除操作中保证树平衡的重要步骤，其条件是目标节点的关键字数量低于最小值。具体操作如下：

1. 从兄弟节点借用一个关键字，或者将目标节点与其左右兄弟节点合并。
2. 若目标节点的左右兄弟节点关键字数量恰好等于最小值，则合并后中间的关键字需要上移至父节点。
3. 如果父节点因合并而关键字数量不足，需要递归地进行合并操作。

def merge_node(left_node, right_node):
    t = left_node.t
    left_node.keys += right_node.keys[:t-1]  # 将右节点的前t-1个关键字合并到左节点
    left_node.children += right_node.children[:t]  # 合并子节点
    return left_node

def borrow_from_left(parent_node, node_index):
    # 借用左兄弟节点的关键字，并将父节点中的一个关键字下移
    # 具体实现省略，需要调整父节点和兄弟节点的相关信息
    pass

def borrow_from_right(parent_node, node_index):
    # 借用右兄弟节点的关键字，并将父节点中的一个关键字下移
    # 具体实现省略，需要调整父节点和兄弟节点的相关信息
    pass

在该示例中，我们提供了节点合并的函数 merge_node 。同样，省略了父节点和子节点调整的细节。

接下来，我们将探讨B树查找操作与效率分析。

4. B树的查找操作与效率分析

B树作为一种自平衡的树数据结构，广泛应用于数据库和文件系统的索引中。它通过将数据分成块、以块为单位存储和索引，能够保持树的平衡，从而确保在最坏情况下也能保持较高的查询效率。

4.1 B树的查找过程详细解析

4.1.1 查找算法的工作原理

B树的查找算法从根节点开始，根据所查找的键值与节点中数据项的比较结果，决定向下访问哪一个子节点。在查找过程中，算法逐层向下，直至找到目标数据项或确定该数据项不存在为止。每次比较操作都旨在缩小查找范围，逐步逼近目标数据。

def b_tree_search(root, key):
    current = root
    while current is not None:
        index = 0
        while index < len(current.keys) and key > current.keys[index]:
            index += 1
        # If the key is found, return its value
        if index < len(current.keys) and key == current.keys[index]:
            return current.values[index]
        # Move down to the next child node
        current = current.children[index] if index < len(current.children) else None
    return None # Key not found

在上述代码中， root 是 B树的根节点， key 是需要查找的目标键值。函数从根节点开始，在每个节点内通过循环查找目标键值，每次循环将当前节点的键值与目标键值进行比较。若目标键值小于当前节点的某个键值，则向左子节点移动，若大于则向右子节点移动，若等于则返回对应值。如果当前节点的所有键值都比较完毕仍未找到目标键值，则向下一个子节点移动。若到达叶子节点仍未找到，则返回 None。

4.1.2 查找路径的选择和优化

B树的查找效率取决于树的高度和节点中的键值数量。B树优化查找路径的主要方法是尽可能减少查找深度，这意味着要确保树的高度尽可能低。由于B树是多路平衡树，它通过分裂和合并节点来保持树的平衡性，从而保持较低的树高。

为了优化查找路径，设计者需要合理选择B树的阶数（即节点允许的最大子节点数）。阶数越高，单次磁盘I/O可以读取更多的数据，但是节点内部查找的代价也相对增加。通常，系统会根据实际应用场景和存储设备的特性来确定最优阶数。

4.2 B树高度对查找效率的影响

4.2.1 高度与查找时间复杂度的关系

在B树中，树的高度决定了数据查找时需要进行的I/O操作次数，因为一次I/O操作只能访问树的一层。树的高度越高，查找操作所需的I/O次数就越多，查找效率也就越低。

在最坏的情况下，B树的高度与树的阶数（ t ）和数据记录数（ n ）之间有如下关系： [ h \leq log_t ((n+1)/2) ] 其中， h 为树的高度， t 为阶数， n 为数据记录数。通过这个关系可以看出，B树的高度随着阶数的增加而减少，但这并不意味着阶数越大越好，因为节点的存储空间和处理能力是有限的。

4.2.2 如何通过平衡降低B树高度

为了保持B树的平衡，避免树过高，需要在插入或删除节点时执行节点的分裂和合并操作。这些操作确保了B树维持平衡的特性，同时也控制了树的高度。当节点的键值数量达到最大值时，将节点分裂成两个节点，并在父节点中添加一个键值作为分隔。相反，当节点的数量低于最小值时，将与相邻的节点进行合并。

为了保持B树的平衡，还需要在每次修改后进行回溯检查。如果发现父节点分裂或子节点合并导致不平衡，需要继续进行平衡操作，直到整棵树达到平衡状态。这种递归式的平衡维护策略，确保了B树在动态变化的数据集上的高效性能。

以下是B树操作的伪代码，强调了在插入和删除过程中对树高度影响的控制：

flowchart TB
    A[开始] --> B[查找插入位置]
    B --> C{是否满节点?}
    C -- 是 --> D[节点分裂]
    C -- 否 --> E[插入数据]
    D --> F[是否需要递归分裂?]
    F -- 是 --> G[递归分裂]
    F -- 否 --> H[结束分裂过程]
    G --> H
    E --> I[结束插入过程]
    H --> I
    I --> J[检查树的平衡性]
    J -- 平衡 --> K[完成操作]
    J -- 不平衡 --> L[节点合并或重新平衡]
    L --> K
    K --> M[结束]

通过这种方式，B树能够在数据更新的同时保持较低的高度，确保了查找效率。在实际应用中，通过精心设计和调整B树的阶数和平衡策略，可以在保持高效查找性能的同时，减少I/O操作次数，提高系统整体性能。

5. B树的平衡性与优化特性

5.1 B树的平衡性特征和维护

5.1.1 平衡性的数学描述

在数据结构中，平衡性是一个关键的概念，它确保了操作的效率和数据访问的优化。在B树中，平衡性确保了所有的叶子节点都位于同一层级，从而使得查找、插入和删除操作能够以对数时间复杂度执行。B树的平衡性可以通过一个称为“平衡因子”的概念来数学描述，平衡因子是指任何节点的子节点数目的最小值和最大值之间的差异。

在理想的平衡B树中，所有非叶子节点都具有 t-1 至 2t-1 个子节点，其中 t 是树的最小度数。这也意味着任何两个叶子节点之间深度的最大差异不会超过1。这样的结构保证了B树在数据分布不均匀时仍能高效运行。

5.1.2 平衡调整方法及其必要性

为了维持B树的平衡性，当进行插入或删除操作时，可能需要调整树的结构。节点的分裂和合并是B树维护平衡的主要操作。

• 节点分裂 ：当一个节点的关键字数量超过最大值 2t-1 时，需要将节点分裂成两个节点，每个节点保持 t-1 至 2t-1 个关键字。
• 节点合并 ：当一个节点的关键字数量低于最小值 t-1 ，且其相邻兄弟节点中有足够多的关键字可以共享时，可能会发生节点的合并。

调整过程可以形象地用以下伪代码表示：

function splitNode(node):
    if node is not a leaf:
        for each key in node:
            create a new node with the higher keys from key
        node retains the lower keys
    else:
        redistribute keys between node and a sibling node

function mergeNodes(node1, node2, parentKey):
    if node1 and node2 are both leaf nodes:
        node1 += node2 and remove key from parent
    else:
        move keys between node1 and node2 to balance them
        update parentKey if necessary

调整过程保证了B树在高度上的平衡性，从而维护了其优越的性能。

5.2 B树的优化应用与前景展望

5.2.1 B树在不同领域的优化应用案例

B树作为一种高效的数据结构，在多个领域中都有广泛的应用。以下是一些优化应用案例：

• 数据库索引 ：在数据库系统中，B树被用作索引结构，用于提高查询速度和管理数据项的快速访问。
• 文件系统 ：B树能够有效地管理磁盘空间，优化存储设备的数据访问，因此在许多现代文件系统中，B树是核心组件之一。
• 内存管理 ：在虚拟内存系统中，B树用于管理内存页表，以快速地完成地址转换和数据访问。

5.2.2 B树研究的新趋势与未来展望

随着数据量的持续增长，B树的优化和变种继续受到关注。以下是一些研究的新趋势：

• B+树和B*树 ：B+树和B*树是B树的变种，它们通过优化节点之间的连接和数据存储方式，提高了在大规模数据集上的性能。
• LSM树 ：日志结构合并树（LSM树）是一种为了解决写入性能问题而设计的数据结构，它结合了B树和日志文件的优势。
• 多维B树 ：为了处理多维空间数据，例如地理信息系统（GIS）中所使用的数据，研究人员正在开发和改进能够有效地处理多维数据点的B树变种。

这些新趋势和优化策略正不断推动B树结构的发展，使其在处理大数据和快速查询响应方面更具竞争力。未来，随着存储技术的进步和应用需求的提升，B树及其变种仍将是数据管理领域的核心研究课题。

本文还有配套的精品资源，点击获取

简介：B树是一种平衡多路查找树，广泛应用于数据库和文件系统中，以实现高效的数据排序和操作。本资源通过Flash动画展示B树如何动态调整结构来应对数据的插入和删除。该演示详细解释了B树的构造、插入和删除操作、查找过程、树高影响以及其平衡性质，帮助学习者通过视觉体验深入理解B树的工作原理。

本文还有配套的精品资源，点击获取