
圆中阴影部分面积求法的常用方法

一、利用规则图形的和差求面积:
例题1、如图、在边长为 4 的正方形ABCD中,先以点 A 为圆心,AD 的长为半径画弧,在以 AB 的中点为圆心,AB 长的一半为半径画弧,则阴影部分面积是多少?(结果保留 π)
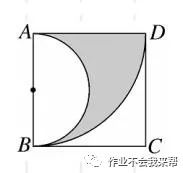
图(1)
解:
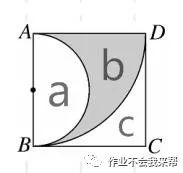
图(2)
Sa + Sb = S扇形ABCD ;
Sb = S扇形ABCD - Sa = 1/4 π × 4 × 4 - 1/2 π × 2 × 2 = 2π 。
例题2、如图、矩形ABCD的边长BC为3 cm,宽 AB 为 2 cm, 点 E、F 是边 AD 的三等分点,点 G、H 是边 BC 的三等分点。现分别以 B、G 两点为圆心,以 2 cm 长为半径画弧 AH 和弧 EC ,则图中阴影部分的面积为多少平方厘米?
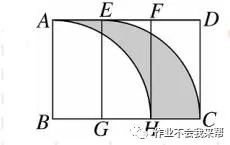
图(3)
解:∵四边形ABCD是矩形,点 E、F是边AD的三等分点,点 G、H是边AD的三等分点 ,BC = 3 cm,
∴ AE = EF = BG = GH = 1 cm ,S扇形ABH = S扇形EGC ,四边形ABGE是矩形。
∴S阴影 = S矩形ABGE + S扇形EGC - S扇形ABH = S矩形ABGE = 2×1 = 2 (cm^2 )。
例题3、如图 C 为半圆内一点,O 为圆心,直径 AB 长为 2 cm , ∠BOC= 60°, ∠BCO = 90°,将△BOC绕圆心O逆时针旋转至△B'0C' ,点 C' 在OA 上,则边 BC 扫过区域(图中阴影部分)的面积是多少?
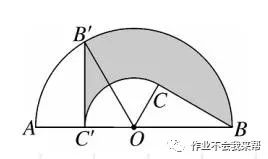
图(4)
解:

图(5)
二、割补法:
例题4、如图、在扇形AOB中,∠AOB= 90°,正方形CDEF 的顶点 C 是AiB弧 的中点,点 D 在OB 上,点 E 在OB的延长线上,当正方形 CDEF 的边长为 2√2 时,则图中阴影部分的面积是多少?(结果保留 π)
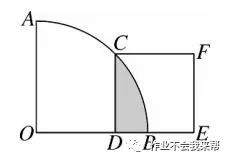
图(6)
解:
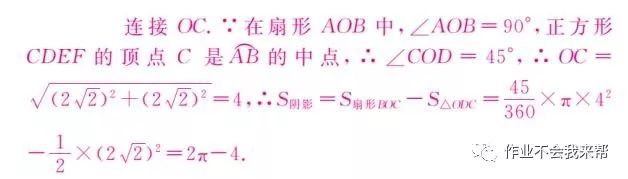
图(7)
三、等积法:
1、轴对称等积法:
例题5、如图、小方格都是边长为 1 的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”图形(阴影部分)部分的面积是多少?(结果保留 π)
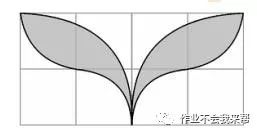
图(8)
解:
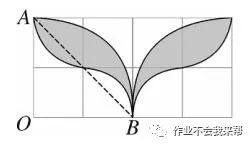
图(9)
如图,连接AB,则阴影部分的面积为 :2 (S扇形AOB - S△AOB)= 2π - 4 。
2、旋转等积法:
例题6、如图、以AB为直径,点O 为圆心的半圆经过点C,若 AC = BC = √2 ,则图中阴影部分的面积是多少?(结果保留 π)。
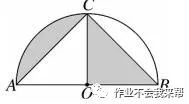
图(10)
解:

图(11)
3、同底等高的三角形等积替换:
例题7、如图、AB是半圆 O 的直径,点 C 、D 是半圆 O 的三等分点,若 旋 CD = 2 ,则图中阴影部分的面积为多少?(结果保留 π)。
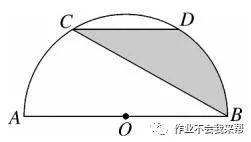
图(12)
解:

图(13)
四、折叠问题中求阴影部分图形的面积:
例题8、如图、半径为 1 的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点 M 与 圆心 O 重合,则图中阴影部分的面积是多少?(结果保留 π)。
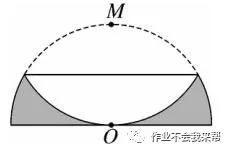
图(14)
解:
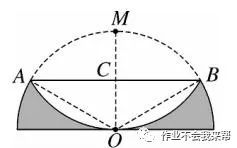
图(15)

图(16)























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








