加密算法程序设计2RSA算法实验报告

一、实验目的

（1）理解公开密钥密码体制的特点。
（2）理解RSA算法的实现过程。
（3）学会用C语言实现RSA算法。

二、实验环境

硬件：运行Windows操作系统的计算机
软件：C语言的编译环境

三、实验原理

RSA算法是1977年由麻省理工学院的Ron Rivest,Adi Shamir 和Leonard Adleman一起提出的非对称加密算法。RSA就是由他们三人姓氏开头字母拼接而成。RSA算法是目前最有影响力的公钥加密算法，它能够抵抗现有的已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。

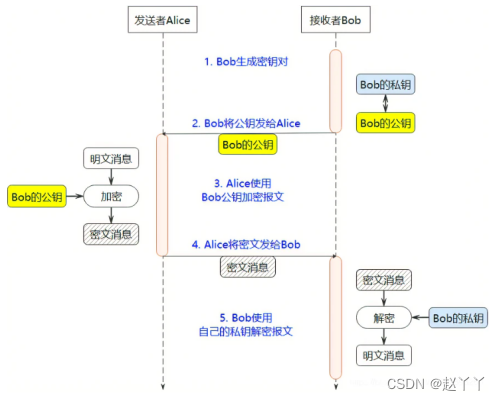
图 1 RSA交互流程
RSA算法给予一个十分简单的数论事实：将两个大素数想成十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。RSA算法主要包括：密钥生成，加密过程和解密过程。
1、密钥计算方法
在秘钥生成过程中，首先生成两个大的质数（素数）p和q，令n=p×q;m=(p-1)×(q-1),选取较小的数e,使e 和m互质，即e和m的最大公约数为1，然后生成d，使d×e mod m=1，最后丢弃P，q，m，则公钥为e，n，私钥为d和n。
2、加密方法
将明文x加密成密文y的计算公式为：x=y^d mod n。从公式可见，加密牵涉到明文和公钥。因此，密文即使被截获，也无法被解读。

图 2 RSA的加密过程
3、解密方法
将密文y解密成明文x的计算公式为：x=y^d mod n。从公式可见，解密至牵涉到私钥和密文。因此，只要保管好私钥，不泄密，就可以放心地把密文和公钥公开。

图 3 RSA的解密过程
4、算法的安全性
RSA算法的安全性依赖于大数分解，但是否等同于大数分解一直未得到理论上的证明，因为还没有证明破解RSA算法一定需要作大数分解。假设存在一种无需分解大数的算法，那它肯定可以修改成为大数分解算法。目前，RSA算法的一些变种算法已经被证明等价与大数分解。
不管怎么，分解大数n是最显然的攻击方法，因此，模数n必须根据使用的场合尽量选大一些，如果主流RSA算法都建立在512bit到1024bit的大数运算之上，对于当前的计算机水平，一般认为只要选择1024bit长的密钥就较难攻破了。
5、算法实例
下面给出一个算法实例。为计算方便，选择较小的质数（实际应用时不安全）。
①密钥生成。首先生成两个大的质数，p=7,q=19，计算n=p×q=133。
计算m=(q-1)×(p-1)=108。选择较小的数e=5，使e和108互质，然后生成d，使d×e mod n=1，计算得到d=65，至此，公钥e=5,n=133，私钥d=65，n=133，密钥计算完毕。
②加密过程。RSA的原则是明文应该小于p和q的较小者。所以，明文x可取值6。计算密文：y=x^e mod n=6^5 mod 133=62。
③解密过程。计算明文：x=y^d mod n=62^65 mod 133=6。

四、实验步骤及结果

依据上述实验原理，编程实现RSA密码算法。
RSA密钥生成算法具体如下：
（1）随机选取两个素数，作为p和q;
（2）计算n=q×p,m=(q-1)×(p-1)；
（3）随机选取e,使e 与m互质；
（4）利用扩展欧几里得算法，计算d使d×e mod m=1；
（5）得到公钥(e,n)和私钥(d,n)。
RSA加密算法具体如下：
（1）输入明文x(数字)；
（2）利用模运算的性质，计算密文y=x^e mod n。
RSA解密算法具体如下：
（1）输入密文y（数字），
（2）利用模运算的性质，计算密文x=y^d mod n。

五、实验总结

1、实验过程中遇到的问题及解决办法；
（1）对于算法的原理和具体的实现不是很熟练，查阅相关资料对过程有了很详细的理解，包括源代码中所需的具体定义及函数。
（2）进行加密解密过程中，手动计算多次幂模运算较为复杂，计算机运算很快，所以报告中举例采用较小的素数，计算时参考课本中的迭代运算方法。
2、设计及调试过程中的心得体会。
通过本次实验，我对RSA算法的原理和实现过程更加了解，会运用一些现成的算法进行编程，对一些比较复杂的算法开始基本认识并掌握，在以后所涉及这方面的知识将会有全新的了解和掌握。相对于DES算法，RSA加密和解密的密钥不一样，但是密钥尺寸大，加解密速度慢。这个实验的算法相对来说较容易实现，但真正掌握这个算法还是 需要对算法进行深入的分析，在过程中需要特别注意细节。