java-求二叉树节点个数 / 叶子节点个数 / 第k层节点个数

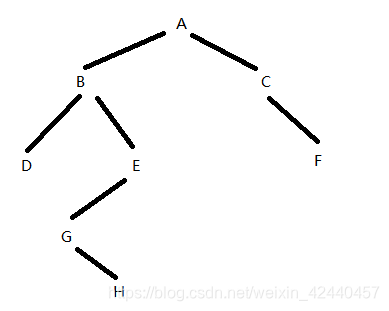
    public static int size(Node root) {
        //求二叉树中节点的个数
        //使用先序遍历的方式
        if (root == null) {
            return 0;

        }
        //体会递归"拆分问题的过程
        //整个树节点个数=根节点的个数(1)+左子树的个数+右子树的个数
        return 1+size(root.left)+size(root.right);


    }

    public  static  int leafSize(Node root){

        //求二叉树叶子节点的个数
        //还是要遍历树,并且拆分问题
        if (root==null){
            return 0;
        }
            if (root.left==null&&root.right==null){
                //此时的root没有子树,root自己就是叶子节点.
                return 1;
            }
            return leafSize(root.left)+leafSize(root.right);


    }

    public static int  kLevelSize(Node root,int k){
        //求二叉树第K层的节点个数
        //如果k<1 那么只能是空树,直接返回0;
        //如果k==1 求根节点的个数.直接返回1
        //k层节点的个数=根节点左子树的k-1层节点个数+根节点右子树的k-1层节点个数

        if (k<1){
            return 0;
        }
        if (k==1){
            return 1;
        }
        return kLevelSize(root.left,k-1)+kLevelSize(root.right,k-1);


    }