数学统计--标准分数

1 定义

变量值与其平均数的离差除以标准差后的值称为标准分数（standard score），也称标准化值或z分数。设标准分数为z，则有 $$z_i=\frac{x_i-\bar{x}}{s}$$

标准分数给出了一组数据中各数值的相对位置。比如，某个数值的标准分数为-1.5，就知道该数值低于平均数1.5的标准差。这个式子也是我们常用的统计标准化公式，在对多个具有不同量纲的变量进行处理时，常常需要对各变量进行标准化处理。

2 性质

标准分数具有平均数为0，标准差为1的特性，事实上，z分数只是将原始数据进行了线性变换，他并没有改变一个数据在数据中的位置，也没有改变数据分布的形状，而只是将改组数据变为平均数为0，标准差为1.

3 实验

为了证明标准化不会改变原始数据的分布，我们用代码进行了测验：

In [73]:a = np..random.randint(0,10,100)
In [74]:plt.hist(a)
Out[74]: 
(array([ 6., 12., 12.,  5., 13., 12., 12., 11.,  4., 13.]),
 array([0. , 0.9, 1.8, 2.7, 3.6, 4.5, 5.4, 6.3, 7.2, 8.1, 9. ]),
 <BarContainer object of 10 artists>)

原始分布:

将原始样本进行标准化处理：

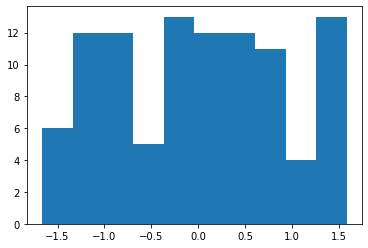
In [75]:plt.hist((a-np.mean(a))/np.std(a))
Out[75]: 
(array([ 6., 12., 12.,  5., 13., 12., 12., 11.,  4., 13.]),
 array([-1.66371794, -1.338914  , -1.01411007, -0.68930613, -0.3645022 ,
        -0.03969826,  0.28510568,  0.60990961,  0.93471355,  1.25951749,
         1.58432142]),
 <BarContainer object of 10 artists>)

标准化后的分布：

4 表述方法

我们通常可以这么描述标准分数：
约有70%的数据在平均数±2个标准差的范围之内
在±3个标准差之外的数据我们称为离群点（outlier）
某样本标准分数的绝对值越大，表示该样本离整体数据中心越远。

参考：
https://www.zhihu.com/question/21600637