两个运放制作加法器_有人用三维动画，一次性帮你把运放讲明白了

假设有一个电压，我们称它为输入，我们把这个输入乘以一个数字来产生另一个电压，我们称它为输出

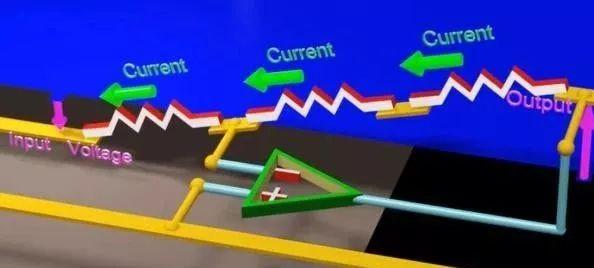
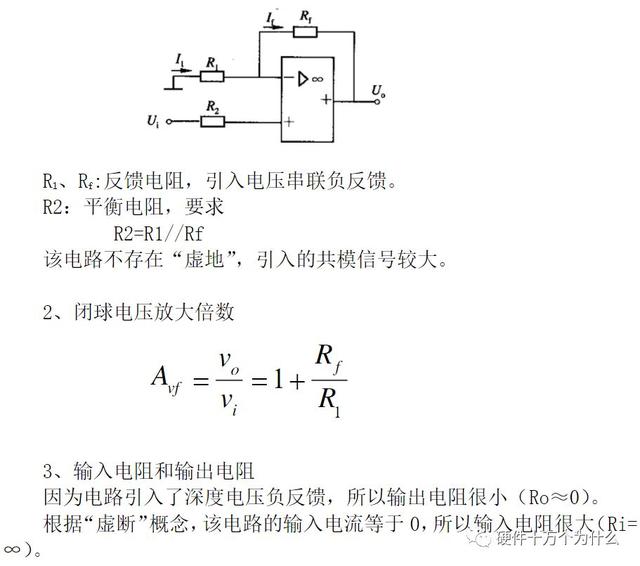
我们实际使用过程中，知道虚短：-反相输入端和 + 同相输入端的电压相等。

如果我们把+同相输入端的电压固定住，负输入端的电压也就被固定住了，如同动画里面的跷跷板原理。输出电压就被放大了！

或者，有几个输入电压，我们希望把它们相加，输出电压代表它们的和，即加法器。基于电阻阻值相同的情况下，视频中的公式成立。

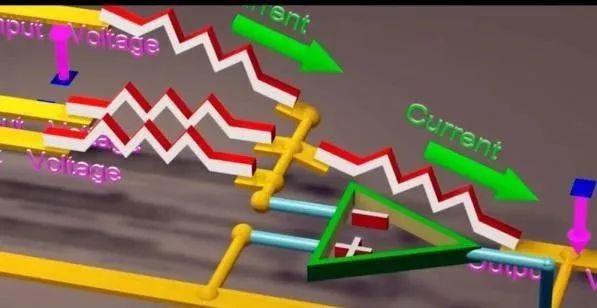
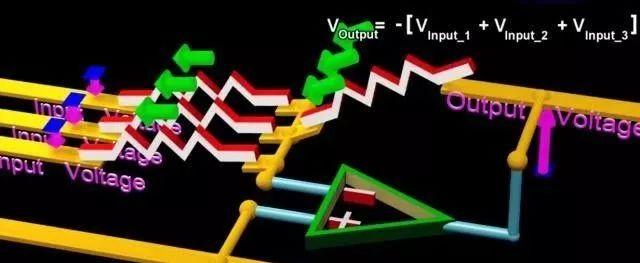
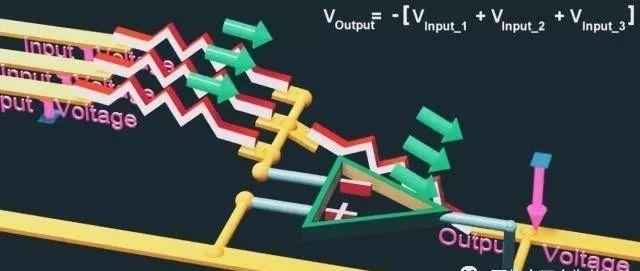
像这样的操作，以及许多更高级的计算，可以用运算放大器的电路来执行，我们通常称为运算放大器。

熟悉电子电路的朋友很容易知道如下图就是积分器

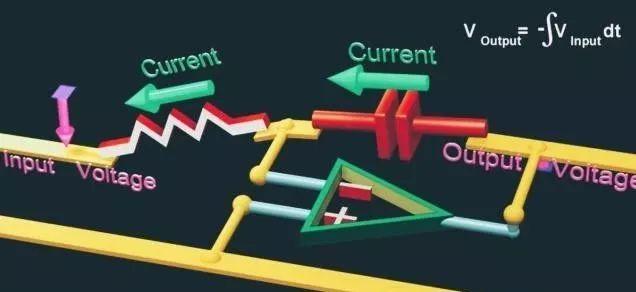
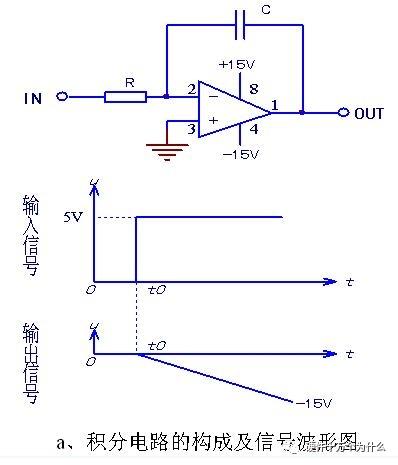
如视频中所示，输出信号不是立即变化变成输入信号的N倍，而是一个累积渐变的过程，我们通过上面的图也可以看到这个过程。

在演示了几个基本的运放电路之后，视频中开始细致展开分析运放电路。

我们本篇讨论具有“理想运放的电路”运算放大器有两个输入端和一个输出端。

首先介绍的现象叫做：虚断！ 电流不能流进或流出输入端子

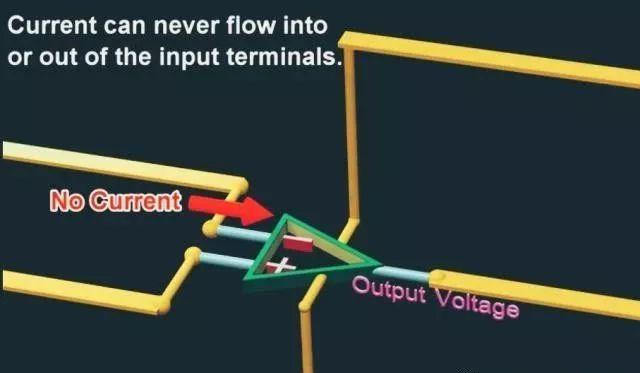
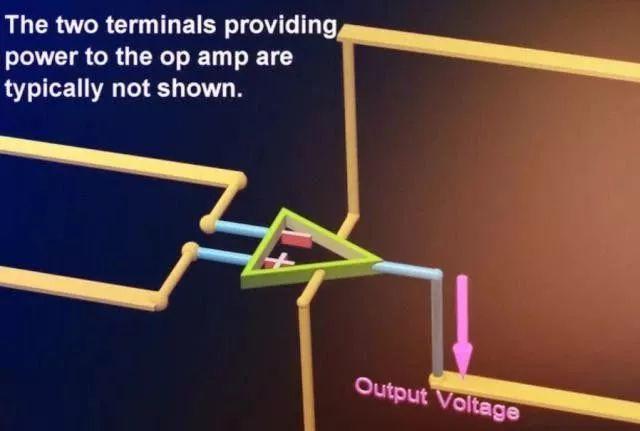
但电流可以流入和流出输出端子，输出端子或流出的电流由两个终端提供给运放

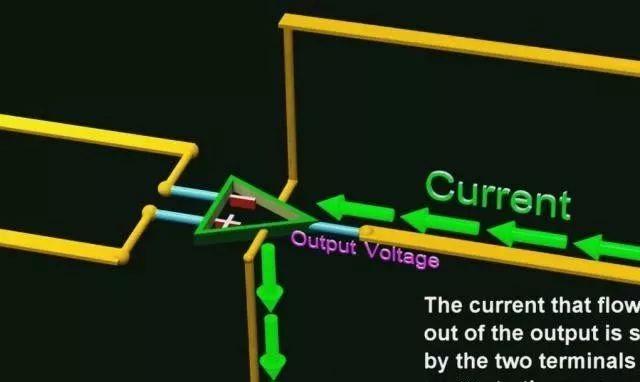
在教科书上，我们有时看到运放的两个电源管脚没有被画出来。所以误导了有些朋友刚接触电路的时候，认为输出的电压范围没有什么限制。

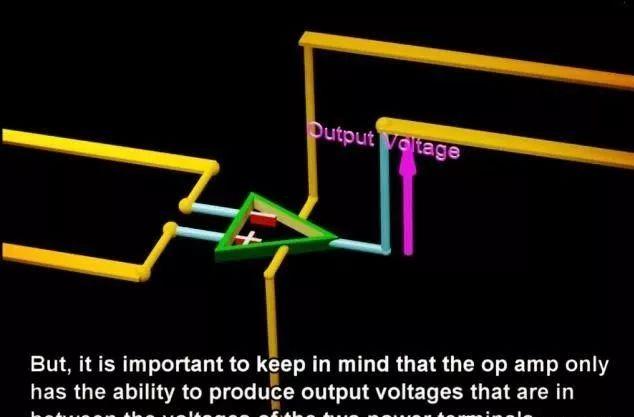
实际上，运放的输出电路，但是重要的是运算放大器只能够产生两个电源端子之间的输出电压。如果是正负电源，我们的输出最高到正电源，最低到负电源。如果是单电源供电，最小就是GND。

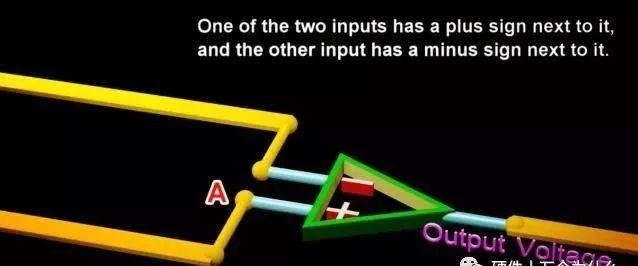
两个输入中的一个在它旁边有“+”，另一个输入在它旁边有“-”号

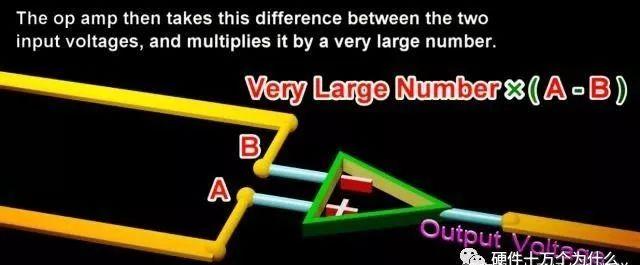
“+”的输入电压值减去它的“-”的输入电压值

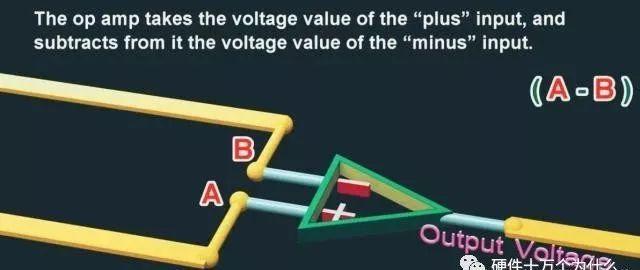
运算放大器将这两个输入电压之间的差值，乘以一个非常大的数，运算放大器使得输出电压等于这个值。

我们把这个没有接反馈电阻的电路，看成是负输入端和输出之间跨接了一个无穷大的电阻，按照我们熟知的理论，应该把输入电压放大无穷大倍。

但是现实过程中，没有那么理想！当输出电压信号“顶天立地”之后，就再也不能继续增大。所谓顶天立地就是达到或者接近了正负电源的电压值。

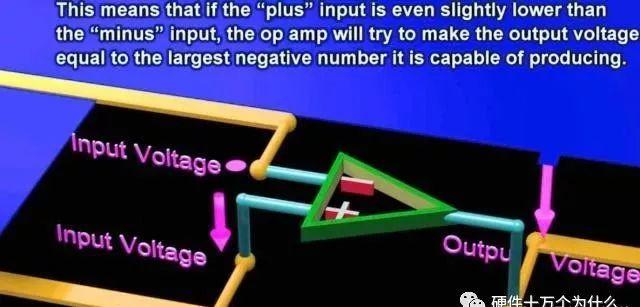
这就意味着，如果“+”输入比“-”输入略低，运算放大器将使输出电压等于它能够产生的最大负数

如果“+”输入略高于“-”输入，运算放大器将使输出电压等于它能够产生的最大正数

现在我们一起来研究一下“负反馈”。

这两个电阻的阻值会决定输出电压的电压值。

在动画中，用跷跷板效应演示的非常形象。运算放大电路分析的时候，我们往往在上学时容易套公式。其实我们在运用公式之前，一定要确定清楚，哪些电压值是确定的，然后再套用公式。

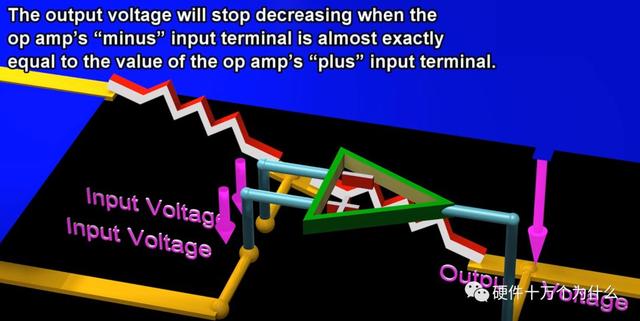
当+端电压下降的时候，由于我们知道的：虚短，-端的电压会追随+端的电压同时也电压下降。

同时，由于我们知道的虚断。左侧电阻上面的电流不会流入运放，会通过反馈电阻，即右侧电阻保持电流大小和流向。

同样的如果+端电压抬高，-端的输入电压也跟随变大。同时输出电压也变大了。

例如，+端的电压为0V保持不变，则-端的电压就会也为0V保持不变。

当输入电压下图中通过电阻接到-端的电压变化的时候，就会导致输出电压随之变化。

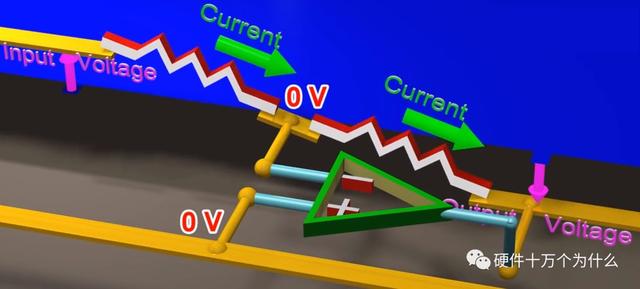
视频中的跷跷板动画非常生动的展示了变化。

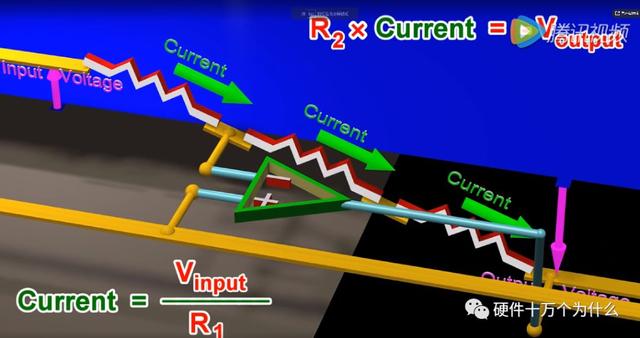
根据虚断、虚短，基尔霍夫定律，则上图公式表示了输出电压与输入电压的关系。

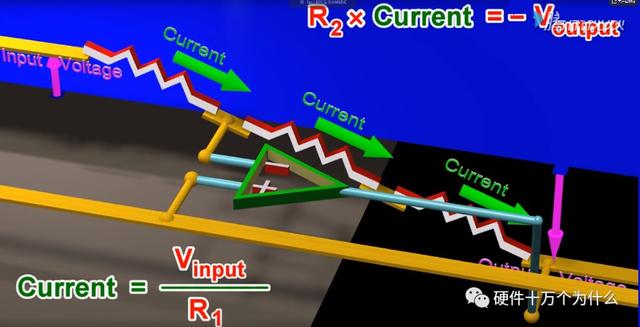
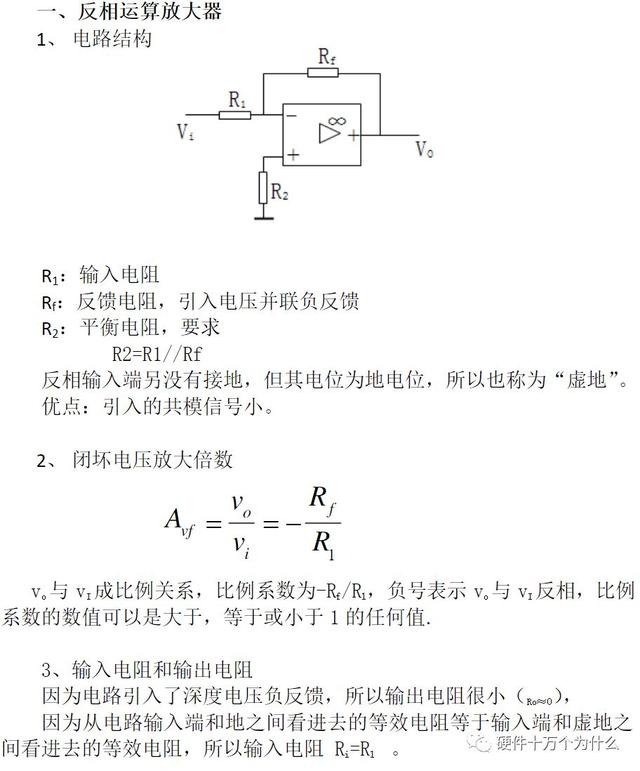
同样的原理，我们在这个电路中，把-输入端的电阻的一端接地，即为0V

此时我们变化+端的电压，可以知道-端的电压会跟随+的端电压变化。

此时我们用一样的分析方法，可以知道输出电压的值。

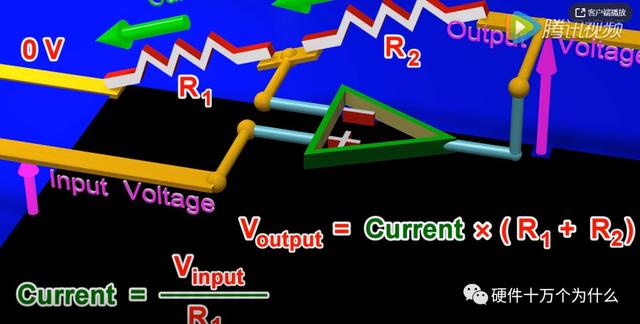
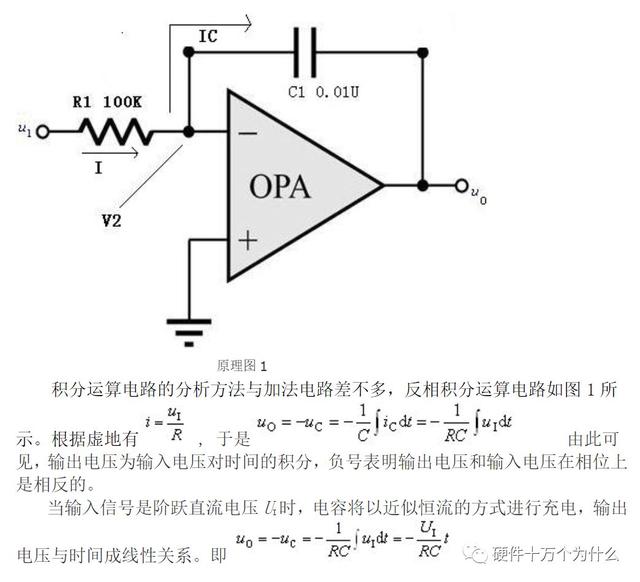
同样分析积分电路，只不过跨接的反馈电阻不再是个电阻，而是个电容，此时电流的计算方法为电容的欧姆定律。如下图所示。

则输出电压为：

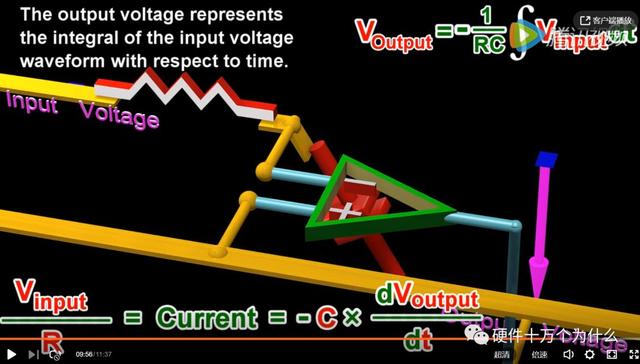
同样的道理，我们把电容放置在另外一个位置，就形成了微分电路。

如果你理解原理，你一定会觉得视频教程在啰嗦了。跟随电路、加法器电路等等都是一样的分析过程。