随机效应估算与固定效应估算_【讲座Q&A】群体药代动力学模型估算方法发展简史讲座...

1

FOCE与FOCEI的区别？

王世俊 解答：简而言之，FOCE中不考虑随机效应与随机残差的相关性，而FOCEI则会考虑并计算，所以可以通过他们的相关性解释模型的部分变异性，从而提高拟合度。详见NONMEM说明书。

付永超 备注：Phoenix NLME的FOCE ELS算法与NONMEM的FOCE I算法类似。

2

对于稀疏数据，应该使用什么算法呢？

王世俊 解答：FOCE类算法与EM类算法都可以；当FOCE类算法出现问题时，可改用EM类算法，也可直接使用EM类算法，EM算法对于稀疏数据有优势。原因是FOCE算法中对于参数在群体中的分布具有“正态“假设，但对于稀疏数据，有可能出现样本的不均匀性(比如稀疏的样本都出现在正态曲线的一侧)，从而导致FOCE算法出现错误。EM算法的迭代过程可以减轻稀疏样本对于群体信息的扭曲程度。

3

如何判断参数是多峰分布呢？

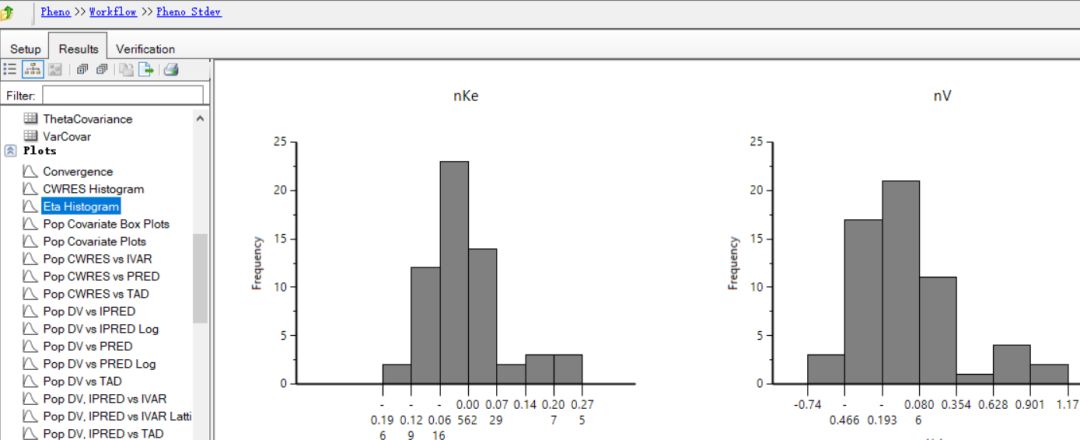
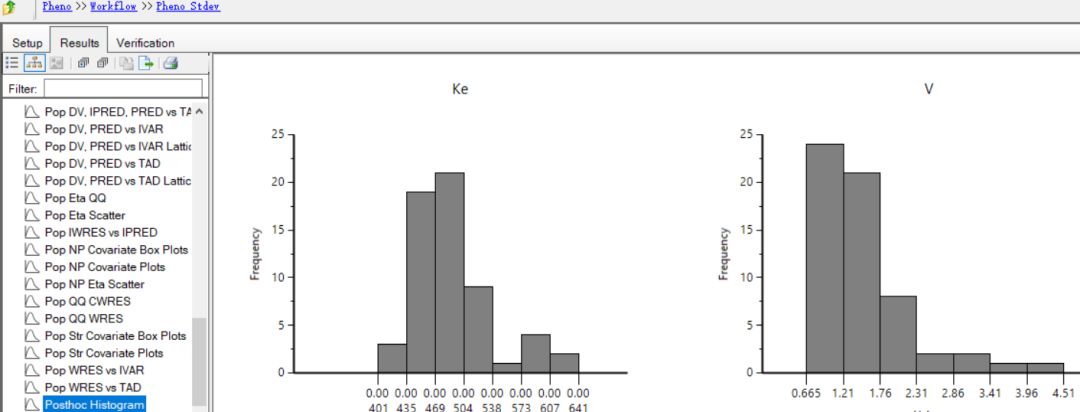
王世俊 解答：模型拟完成后，绘制eta的分布图(直方图)，或者绘制经贝叶斯反馈后得到的个体药动学参数的分布图。如果FOCE算法失效，可以直接用非参数法进行拟合，由于非参数法并没有参数的分布假设，所以可以如实呈现出参数的“多峰“分布而不出现计算错误。发现多峰分布后，可根据需要建立”场合间变异“模型或者”混合分布模型“。

付永超 备注：在Phoenix Model操作对象的“Results(结果)”标签页中，可查看“Eta Histogram”图或者“Posthoc Histogram”图观察Eta的分布或者个体药动学参数的分布。

Eta Histogram图示例

Posthoc Histogram图示例

4

进行协变量的正向纳入逆向剔除的时候，使用EM类的算法会导致OFV不服从卡方分布么？

王世俊 解答：EM算法对于OFV的分布没有影响。不同估算方法对于OFV只是计算方式不同，得到的结果有近似程度的差异，并不会影响OFV的定义，也就不会影响OFV作为统计检验的工具效果。

5

EM类的算法比FOCE类的算法更容易算出参数的CV%(固定效应参数的百分比化的标准误，即固定效应参数的区间估计)么？

王世俊 解答：首先简略介绍一下FOCE与EM算法在计算参数区间的方法。其中FOCE是估算参数点估计的方法，而对于区间估计则有赖于OFV函数的二阶导数(与fisher信息矩阵类似)以及相关的sandwich矩阵的一系列计算；而EM算法则简单的多，直接对所抽取的样本进行统计计算即可。所以在这里需要区分一下使用场景，对于EM与FOCE在计算参数区间(比如CV%)时的差异，最常见的区别就在于模型维度的差别，模型的随机误差参数若大于6(个人经验)，标准误采用三明治矩阵(sandwich)计算很容易出现错误，也就导致FOCE算法的区间估计失败。所以对于高维模型，EM方法求其参数区间估计更稳定。

付永超 备注：在Phoenix Model对象的“Run Options(运行选项)”选项卡下，可通过“Stderr Method(标准误计算方法)”下拉列表，选择使用何种方式计算标准误，选项有“Hessian”、“Sandwich”、“Fisher Score”。

6

FOCE类的算法很难算出CV%(固定效应参数的百分比化的标准误，即固定效应参数的区间估计)的时候，该怎么办？

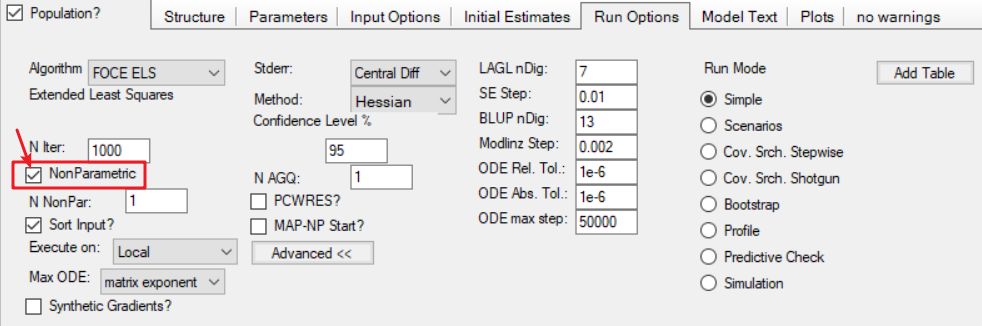
王世俊 解答：进行Bootstrap估算，或者将EM算法迭代次数设置为0，跑一次。原则上主要使用非参数法，规避高维矩阵的计算即可。

付永超 备注：勾选“NonParametric(非参数法)”即可在在结果中获得非参数法计算得到的结果。

7

什么叫“高维”模型？

王世俊 解答：当模型的参数尤其是随机效应相关的参数超过8(个人经验)的时候，设计矩阵计算的参数法会面临很大的不稳定性，这个不稳定性主要来源与逆矩阵的计算过程。

8

建模过程中模型方程的调整方法

王世俊 解答：具体模型具体对待，没有具体的数据，很难谈论输入对模型进行优化。原则上是让OFV减小的基础上，保证模型尽可能简单。

9

算法的收敛判据标准的大小(精度)对结果有什么影响。

王世俊 解答：以FOCE为例，算法收敛的主要参数包括：搜索梯度计算的有效数字、计算搜索步长、搜索停止的宽容度(比如矩阵出现非正定的情况)。整体上对于结果是“得到”和“无法得到”的区别，细节上也可以影响模型是否收敛于局部极值，但搜索过程对于结果的影响十分复杂，无法得出类似于“增加精度得到更好结果”的简单结论(事实上有时候低精度反而容易进入全局极值)

付永超 备注：在Phoenix Model对象的“Run Options(运行选项)”选项卡下，单击“Advavced(高级选项)”按钮后，即可对算法细节包括：“LAGL nDig，输入有效数字位数，以用于LAGL 算法用于达到收敛”、“SE Step，标准误差数值微分步长”、“Modlinz Step，FOCE逼近中线性化模型函数时用于数值微分的步长”，“ODE Rel. Tol.，输入Max ODE的相对公差值”，等等。

10

最终模型估计时，需要用多种算法分别跑下，比较下结果么？

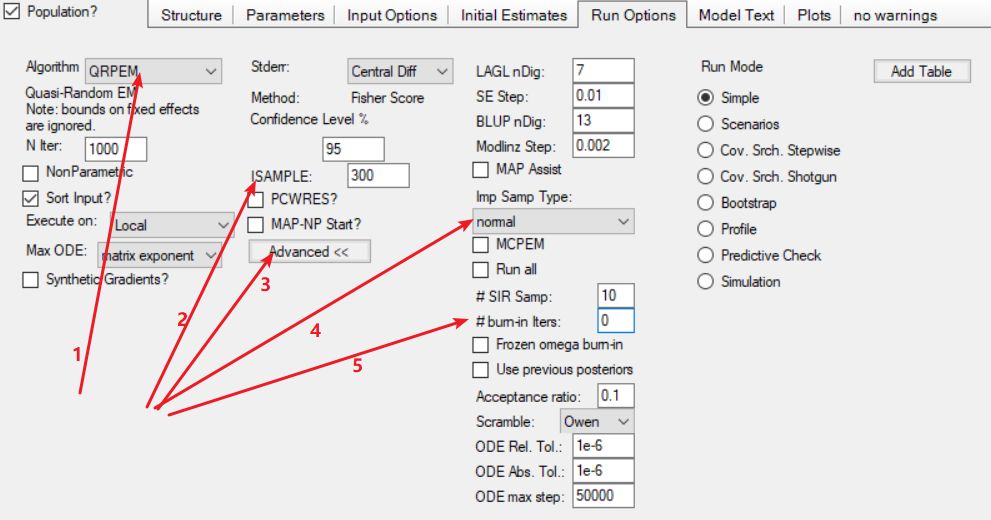
王世俊 解答：这个问题是理想状况，实际上在模型的建立阶段，通常会尝试各种算法提高效率与精准度，所以到了最终模型时算法一般都已经最终确定，继续使用该算法就可；如果建模过程十分顺利，可以再最后利用IMPEM(Importance  Sampling  Expectation  Maxi           mization method，)方法计算精确OFV值并与原本计算方法的结果进行比较，看看是否有较大差距。

付永超 备注：在Phoenix Model对象的“Run Options(运行选项)”选项卡下，“Algorithm(算法)”设置为“QRPEM(拟随机参数期望最大化)”算法，可实现与IMPEM类似功能，可在“ISAMPLE”设置采样的数量，单击“Advavced(高级选项)”按钮后，可以在“Imp Samp Type(重点抽样 抽样类型)” 下拉列表中选择抽样使用的分布，下拉选项包括：normal(多元正态，MVN)、double-exponential(多元Laplace (MVL))、direct()、T(多元T分布，MVT)、mixture-2 (Two-component defensive mixture)、mixture-3 (Three-component defensive mixture)，也可以指定“burn-in(预烧期)”迭代次数。

11

模型的某一随机效应参数的收缩值很大时，该如何处理？

王世俊 解答：首先是某参数收缩值很大(通常指50%以上)时，说明数据里并未包含足够多的信息以支撑模型对该参数进行估计。而有许多不同的原因可以造成这种情况，我在此举一个比较常见的例子：可以在估算结束后，提取出个体参数的估算区间(也就是EBE的不确定度)，然后用该数值与该参数的群体分布方差做比。如此便可以得到数据内各个ID的“个体收缩值”，如果发现数据内某些个体具有非常小的个体收缩值，则说明这些个体的数据包含大量关于该参数的信息。由此，我们可以单独对这些“高信息”个体去提高模型效果。如果个体收缩值普遍比较大，则需要考虑是否需要修改模型取消“高收缩”参数部分。

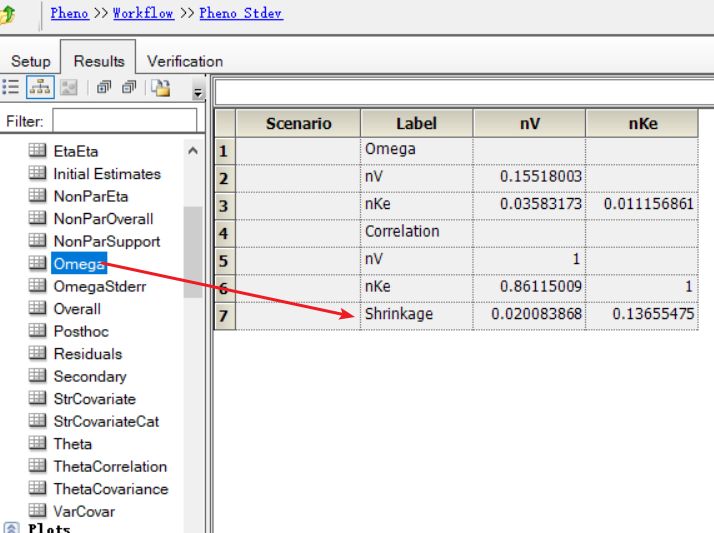
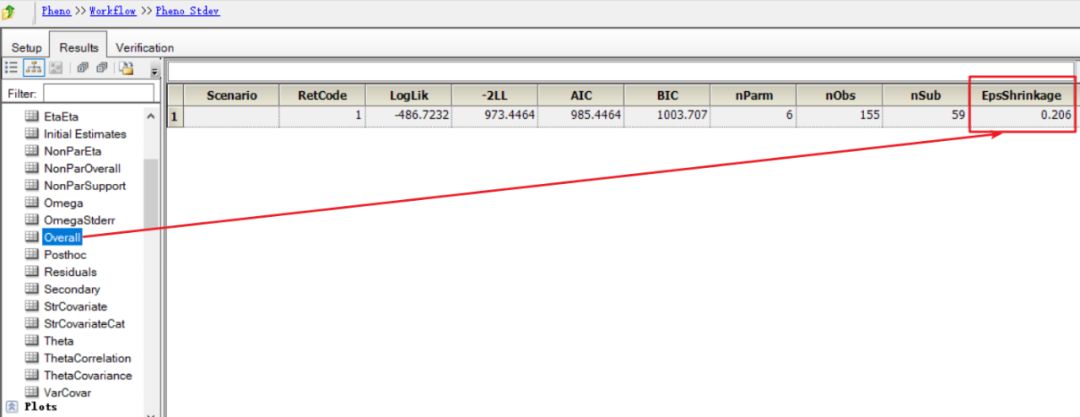
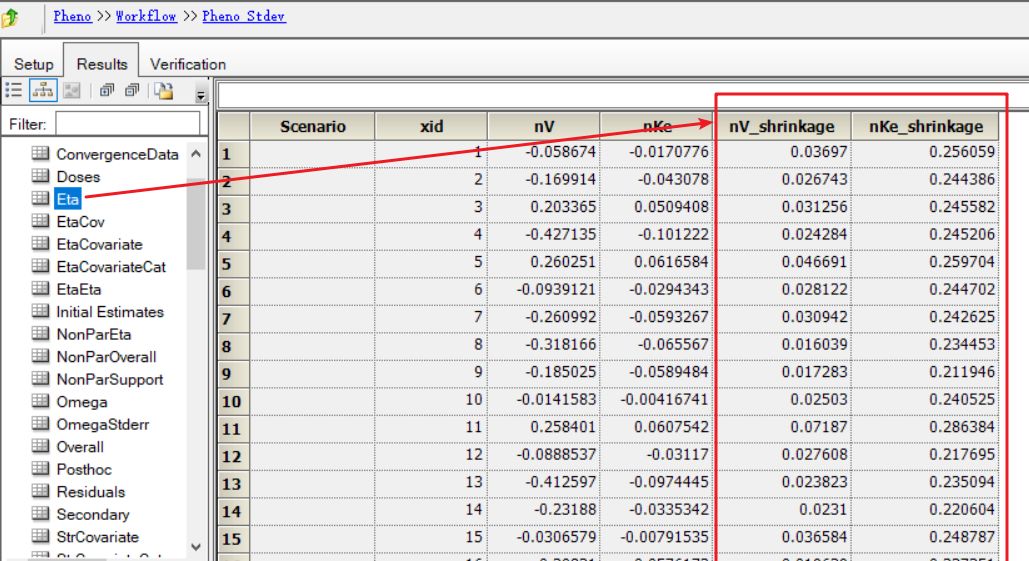
付永超 备注：在Phoenix Model操作对象的“Results(结果)”标签页中，以下位置查看每一类参数的“Shrinkage(收缩)”

个体间变异的随机效应参数的“Shrinkage(收缩)”值：“Omega”表格的最后一行

个体内变异的随机效应参数的“Shrinkage(收缩)”值：“Overall”表格的“EpsShrinkage”列

每个个体的药动学参数的“Shrinkage(收缩)”值：“Eta”表格的最后几列

12

使用EM类算法会影响Bootstrap收敛成功率么？

王世俊 解答：Bootstrap过程，与使用的算法(FOCE类、EM类)无关。

Phoenix新的在线帮助系统网址：

https://onlinehelp.certara.com/phoenix/8.2/index.html

期刊推荐

British Journal of Clinical Pharmacology

Clinical Pharmacology & Therapy

CPT: Pharmacometrics and System Pharmacology

Journal of Pharmacokinetics and Pharmacodynamics

教材：业内并没有一本权威群体药代动力学教材

各个学校(尤其是美国)的pharmacometrics相关硕士项目的课程

生物统计相关教材(尤其是NLME方面)

与本次讲座相关的几篇文章(除此之外可以继续阅读文章的参考文献)：

1、Wang Y. Derivation of various NONMEM estimation methods. J Pharmacokinet Pharmacodyn. 2007;34(5):575–93.

2、Jelliffe R, Schumitzky A, Van Guilder M. Population pharmacokinetics/pharmacodynamics modeling: Parametric and nonparametric methods. Ther Drug Monit. 2000;22(3):354–65.

关于我们

源资信息科技(上海)有限公司成立于2008年5月，公司以协助国内材料、化工、药物开发等行业领域的发展为宗旨，以全球视角的创新理念，为生物研究、制药研发、材料研发、临床试验设计、数据分析，以及企业信息化管理和质量管理等各个领域提供连贯整合性平台解决方案。

公司致力于提供行业领先的定量药理学工作平台与咨询培训服务，拥有Phoenix定量药理学工作平台(Phoenix WinNonlin、Phoenix NLME、Phoenix IVIVC系列)：

• Phoenix WinNonlin产品链接：

• http://www.tri-ibiotech.com/pharsight/product_90.html

• Phoenix NLME产品链接：

• http://www.tri-ibiotech.com/pharsight/product_93.html

• Phoenix IVIVC产品链接：

• http://www.tri-ibiotech.com/pharsight/product_94.html

Pirana定量药理学工作平台：

• Pirana产品链接：

• http://www.tri-ibiotech.com/pkpd/product_112.html

Trial Simulator临床试验模型器等行业内领先的解决方案：

• Trial Simulator产品链接：

• http://www.tri-ibiotech.com/pkpd/product_67.html

Certara药物研发战略咨询服务：

• 服务介绍链接：

• http://www.tri-ibiotech.com/pkpd/product_114.html

并组织与举办了多个相关产品的培训班。