麻省理工学院算法导论课程设计项目实战

本文还有配套的精品资源，点击获取

简介：《算法导论》是计算机科学领域的经典教材，由麻省理工学院（MIT）的知名教授们合著。本课程设计项目经过测试，旨在帮助学生掌握算法设计、分析和实现的广泛主题。通过实践任务，学生将深入理解算法的核心概念，提升解决复杂问题的能力。本项目涵盖了排序与搜索算法、数据结构、分治策略、动态规划、贪心算法、回溯法、分支限界法、图论算法、递归与分形、概率算法、算法设计技巧和计算复杂性理论等关键知识点，为学生在算法领域的学习和应用打下坚实基础。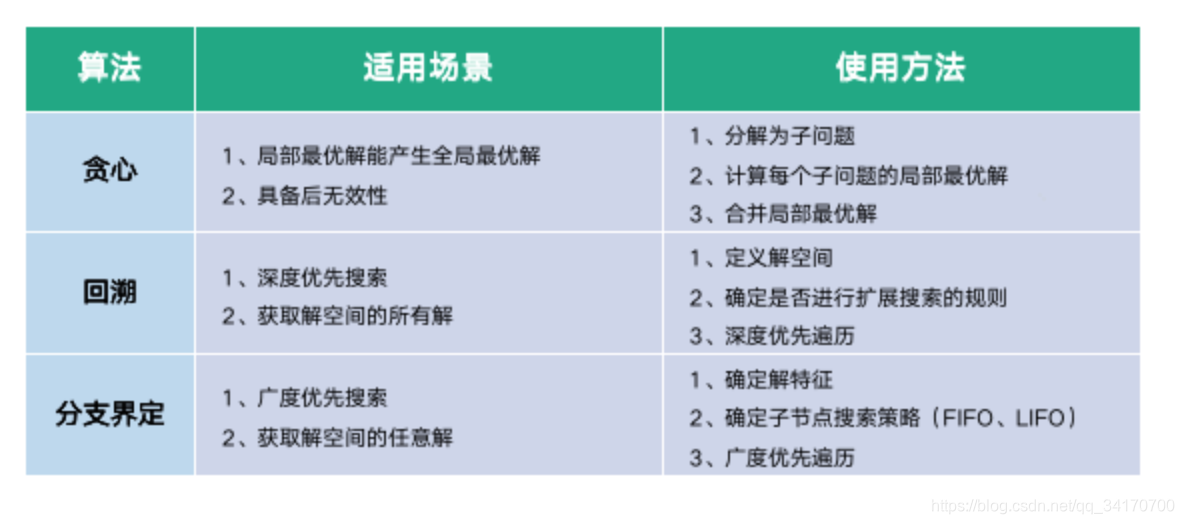

1. 算法基础

算法是计算机科学中解决特定问题的步骤序列。它描述了将输入转换为输出的计算过程。算法基础是理解算法设计和分析的基础。

算法基础包括以下几个方面：

• 基本概念：算法、数据结构、时间复杂度、空间复杂度
• 算法设计：分治、动态规划、贪心算法
• 算法分析：渐近分析、平均情况分析、最坏情况分析

2.2 空间复杂度分析

2.2.1 基本概念和表示方法

空间复杂度衡量算法在执行过程中所需要的内存空间。它通常表示为算法在最坏情况下所使用的内存单元数量。

空间复杂度通常使用大 O 符号表示，例如 O(n)、O(n^2)、O(log n) 等。其中，n 表示算法处理的数据规模。

2.2.2 常见空间复杂度函数

以下是常见的空间复杂度函数：

• O(1) ：表示算法的内存使用量与数据规模无关，始终为常数。
• O(n) ：表示算法的内存使用量与数据规模成正比。
• O(n^2) ：表示算法的内存使用量与数据规模的平方成正比。
• O(log n) ：表示算法的内存使用量与数据规模的对数成正比。
• O(2^n) ：表示算法的内存使用量随数据规模呈指数增长。

代码示例

以下 Python 代码计算一个列表中元素的总和，并分析其空间复杂度：

def sum_list(nums):
    total = 0
    for num in nums:
        total += num
    return total

逻辑分析：

该代码创建一个变量 total 来存储列表中元素的总和。它遍历列表，逐个将元素添加到 total 中。

空间复杂度：

该代码的空间复杂度为 O(1)。这是因为无论列表的大小如何，它始终使用三个变量： total 、 num 和 nums 。

表格示例

下表总结了常见数据结构的空间复杂度：

| 数据结构 | 空间复杂度 | |---|---| | 数组 | O(n) | | 链表 | O(n) | | 栈 | O(n) | | 队列 | O(n) | | 树 | O(n) | | 图 | O(n^2) |

Mermaid 流程图示例

以下 Mermaid 流程图演示了空间复杂度分析的步骤：

graph LR
subgraph 分析空间复杂度
    A[确定算法使用的内存单元] --> B[计算最坏情况下的内存使用量]
    B --> C[使用大 O 符号表示空间复杂度]
end

3. 排序与搜索算法

排序和搜索算法是计算机科学中至关重要的基础算法，它们广泛应用于各种领域，例如数据处理、数据库管理和机器学习。本章将介绍一些常用的排序和搜索算法，分析它们的复杂度并讨论它们的优缺点。

3.1 排序算法

排序算法用于将一个无序序列中的元素按特定顺序排列。常见的排序算法包括：

3.1.1 冒泡排序

算法描述： 冒泡排序通过不断比较相邻元素，将较大的元素向后移动，直到序列完全有序。

时间复杂度： * 最好情况：O(n)（序列已有序） * 平均情况：O(n^2) * 最坏情况：O(n^2)

空间复杂度： O(1)

代码块：

def bubble_sort(arr):
    """
    冒泡排序算法

    参数：
        arr：要排序的列表

    返回：
        排序后的列表
    """
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

逻辑分析： 外层循环控制排序的趟数，内层循环比较相邻元素并交换顺序。

参数说明： * arr ：要排序的列表

3.1.2 选择排序

算法描述： 选择排序通过在序列中找到最小元素并将其与第一个元素交换，然后在剩余序列中找到最小元素并将其与第二个元素交换，依此类推，直到序列完全有序。

时间复杂度： * 最好情况：O(n^2) * 平均情况：O(n^2) * 最坏情况：O(n^2)

空间复杂度： O(1)

代码块：

def selection_sort(arr):
    """
    选择排序算法

    参数：
        arr：要排序的列表

    返回：
        排序后的列表
    """
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

逻辑分析： 外层循环控制排序的趟数，内层循环找到当前最小元素的索引并交换顺序。

参数说明： * arr ：要排序的列表

3.1.3 插入排序

算法描述： 插入排序通过将每个元素逐个插入到已排序的子序列中，从而实现排序。

时间复杂度： * 最好情况：O(n)（序列已有序） * 平均情况：O(n^2) * 最坏情况：O(n^2)

空间复杂度： O(1)

代码块：

def insertion_sort(arr):
    """
    插入排序算法

    参数：
        arr：要排序的列表

    返回：
        排序后的列表
    """
    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

逻辑分析： 外层循环遍历每个元素，内层循环将当前元素插入到已排序的子序列中。

参数说明： * arr ：要排序的列表

3.1.4 归并排序

算法描述： 归并排序是一种分治算法，它将序列递归地分解为较小的子序列，对子序列进行排序，然后合并排序后的子序列。

时间复杂度： O(n log n)

空间复杂度： O(n)

代码块：

def merge_sort(arr):
    """
    归并排序算法

    参数：
        arr：要排序的列表

    返回：
        排序后的列表
    """
    n = len(arr)
    if n <= 1:
        return arr

    mid = n // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])

    return merge(left, right)

def merge(left, right):
    """
    合并两个已排序的列表

    参数：
        left：第一个已排序的列表
        right：第二个已排序的列表

    返回：
        合并后的已排序列表
    """
    i = 0
    j = 0
    merged = []

    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    while i < len(left):
        merged.append(left[i])
        i += 1

    while j < len(right):
        merged.append(right[j])
        j += 1

    return merged

逻辑分析： merge_sort 函数将序列递归地分解为较小的子序列，然后调用 merge 函数合并排序后的子序列。 merge 函数通过比较两个子序列的元素来合并它们。

参数说明： * arr ：要排序的列表 * left ：第一个已排序的列表 * right ：第二个已排序的列表

3.1.5 快速排序

算法描述： 快速排序也是一种分治算法，它通过选择一个枢轴元素，将序列划分为小于和大于枢轴元素的两个子序列，然后递归地对子序列进行排序。

时间复杂度： * 最好情况：O(n log n) * 平均情况：O(n log n) * 最坏情况：O(n^2)

空间复杂度： O(log n)

代码块：

def quick_sort(arr):
    """
    快速排序算法

    参数：
        arr：要排序的列表

    返回：
        排序后的列表
    """
    n = len(arr)
    if n <= 1:
        return arr

    pivot = arr[n // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    return quick_sort(left) + middle + quick_sort(right)

逻辑分析： quick_sort 函数选择一个枢轴元素（ pivot ），将序列划分为三个子序列：小于枢轴元素的子序列（ left ）、等于枢轴元素的子序列（ middle ）和大于枢轴元素的子序列（ right ）。然后递归地对 left 和 right 子序列进行排序。

参数说明： * arr ：要排序的列表

4. 数据结构

数据结构是组织和存储数据的抽象方式，它决定了数据的存储方式和访问效率。在计算机科学中，数据结构是算法的基础，算法的效率和复杂度与数据结构密切相关。本章将介绍各种常见的数据结构，包括线性数据结构和非线性数据结构。

4.1 线性数据结构

线性数据结构是一种按顺序组织数据的结构，其中每个元素都与它的前一个和后一个元素相连。线性数据结构的优点是访问和插入元素都很方便，但查找元素的效率较低。

4.1.1 数组

数组是一种最简单的线性数据结构，它将元素存储在连续的内存空间中。数组中的每个元素都由一个索引值来访问。数组的优点是访问元素非常高效，但插入和删除元素的效率较低。

# 创建一个数组
my_array = [1, 2, 3, 4, 5]

# 访问数组元素
print(my_array[2])  # 输出：3

# 插入元素
my_array.insert(2, 6)

# 删除元素
my_array.remove(4)

4.1.2 链表

链表是一种动态的数据结构，它将元素存储在分散的内存空间中。链表中的每个元素都包含一个数据域和一个指针域，指针域指向下一个元素。链表的优点是插入和删除元素非常高效，但访问元素的效率较低。

# 创建一个链表节点
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# 创建一个链表
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)

# 访问链表元素
current_node = head
while current_node is not None:
    print(current_node.data)
    current_node = current_node.next

4.1.3 栈

栈是一种后进先出（LIFO）的数据结构，它遵循后进先出的原则。栈中的元素只能从栈顶访问和删除。栈的优点是插入和删除元素非常高效，但查找元素的效率较低。

# 创建一个栈
my_stack = []

# 入栈
my_stack.append(1)
my_stack.append(2)
my_stack.append(3)

# 出栈
print(my_stack.pop())  # 输出：3

4.1.4 队列

队列是一种先进先出（FIFO）的数据结构，它遵循先进先出的原则。队列中的元素只能从队列头访问和删除。队列的优点是插入和删除元素非常高效，但查找元素的效率较低。

# 创建一个队列
my_queue = []

# 入队
my_queue.append(1)
my_queue.append(2)
my_queue.append(3)

# 出队
print(my_queue.pop(0))  # 输出：1

4.2 非线性数据结构

非线性数据结构是一种不按顺序组织数据的结构，其中元素之间存在复杂的关系。非线性数据结构的优点是查找元素的效率较高，但插入和删除元素的效率较低。

4.2.1 树

树是一种分层的数据结构，其中每个节点都有一个父节点和多个子节点。树的优点是查找元素的效率较高，但插入和删除元素的效率较低。

# 创建一个树节点
class Node:
    def __init__(self, data):
        self.data = data
        self.children = []

# 创建一棵树
root = Node(1)
root.children.append(Node(2))
root.children.append(Node(3))
root.children[0].children.append(Node(4))
root.children[0].children.append(Node(5))

# 遍历树
def traverse_tree(root):
    print(root.data)
    for child in root.children:
        traverse_tree(child)

traverse_tree(root)

4.2.2 图

图是一种由节点和边组成的非线性数据结构，其中节点表示实体，边表示实体之间的关系。图的优点是查找元素的效率较高，但插入和删除元素的效率较低。

# 创建一个图
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 遍历图
def traverse_graph(graph, start):
    visited = set()
    queue = [start]

    while queue:
        current = queue.pop(0)
        if current not in visited:
            visited.add(current)
            print(current)
            for neighbor in graph[current]:
                queue.append(neighbor)

traverse_graph(graph, 'A')

4.2.3 堆

堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆的优点是查找最小或最大元素的效率很高，但插入和删除元素的效率较低。

# 创建一个堆
heap = [1, 2, 3, 4, 5, 6, 7]

# 上浮操作
def heapify_up(heap, index):
    while index > 0:
        parent_index = (index - 1) // 2
        if heap[index] > heap[parent_index]:
            heap[index], heap[parent_index] = heap[parent_index], heap[index]
            index = parent_index
        else:
            break

# 下沉操作
def heapify_down(heap, index):
    while index < len(heap):
        left_index = 2 * index + 1
        right_index = 2 * index + 2
        largest_index = index

        if left_index < len(heap) and heap[left_index] > heap[largest_index]:
            largest_index = left_index

        if right_index < len(heap) and heap[right_index] > heap[largest_index]:
            largest_index = right_index

        if largest_index != index:
            heap[index], heap[largest_index] = heap[largest_index], heap[index]
            index = largest_index
        else:
            break

# 插入元素
heap.append(8)
heapify_up(heap, len(heap) - 1)

# 删除元素
heap.pop(0)
heapify_down(heap, 0)

5. 分治策略

5.1 分治算法的基本思想

分治算法是一种将大问题分解成一系列较小的问题，然后递归地求解这些较小的问题，最后将这些较小问题的解组合起来得到大问题的解。分治算法的思想主要包括以下几个步骤：

1. 分解： 将大问题分解成一系列较小的问题，这些较小的问题规模较小，更容易求解。
2. 解决： 递归地求解这些较小的问题。
3. 合并： 将较小问题的解组合起来得到大问题的解。

分治算法的优点在于其时间复杂度通常较低，并且易于实现。

5.2 分治算法的应用

分治算法可以应用于各种问题，以下列举几个常见的应用：

5.2.1 归并排序

归并排序是一种基于分治思想的排序算法。其基本思想是：

1. 将待排序的数组分成两半。
2. 递归地对两半进行排序。
3. 将排序后的两半合并成一个有序的数组。

归并排序的时间复杂度为 O(n log n)，其中 n 为数组的长度。

5.2.2 快速排序

快速排序也是一种基于分治思想的排序算法。其基本思想是：

1. 选择一个基准元素。
2. 将数组中的元素分成两部分：一部分小于基准元素，一部分大于基准元素。
3. 递归地对两部分进行排序。

快速排序的时间复杂度为 O(n log n) 的平均时间复杂度，但最坏情况下的时间复杂度为 O(n^2)。

5.2.3 矩阵乘法

矩阵乘法也可以使用分治算法进行优化。其基本思想是：

1. 将两个矩阵分成四个子矩阵。
2. 递归地对四个子矩阵进行乘法。
3. 将四个子矩阵的乘积合并起来得到两个矩阵的乘积。

使用分治算法进行矩阵乘法的时间复杂度为 O(n^3)，其中 n 为矩阵的阶数。

6. 动态规划

6.1 动态规划的基本思想

动态规划是一种解决最优化问题的技术，它将问题分解成一系列子问题，然后依次解决这些子问题，并存储子问题的最优解，以避免重复计算。动态规划的思想可以总结为以下几个步骤：

1. 定义子问题： 将原问题分解成一系列相互独立的子问题，这些子问题可以递归地解决。
2. 建立状态： 定义子问题的状态，即描述子问题所需的信息。
3. 确定状态转移方程： 推导出子问题的最优解与之前子问题的最优解之间的关系，即状态转移方程。
4. 初始化： 确定子问题的初始状态和最优解。
5. 递推： 从初始状态开始，依次计算每个子问题的最优解，并存储这些解。
6. 回溯： 从最终状态出发，通过状态转移方程回溯，得到原问题的最优解。

6.2 动态规划的应用

动态规划广泛应用于解决各种最优化问题，以下是一些常见的应用场景：

6.2.1 最长公共子序列

问题描述： 给定两个字符串，求它们的最长公共子序列，即两个字符串中长度最长的公共子串。

动态规划解法：

1. 定义子问题： 对于字符串 s1 和 s2 的前 i 和 j 个字符，求它们的最长公共子序列的长度。
2. 建立状态： 状态 dp[i][j] 表示字符串 s1 的前 i 个字符和字符串 s2 的前 j 个字符的最长公共子序列的长度。
3. 确定状态转移方程：
4. 如果 s1[i] == s2[j] , dp[i][j] = dp[i-1][j-1] + 1
5. 否则， dp[i][j] = max(dp[i-1][j], dp[i][j-1])
6. 初始化： dp[0][0] = 0
7. 递推： 从 dp[1][1] 开始，依次计算每个 dp[i][j] 。
8. 回溯： 从 dp[m][n] 开始，通过状态转移方程回溯，得到最长公共子序列。

6.2.2 背包问题

问题描述： 给定一组物品，每个物品有其重量和价值，以及一个背包容量，求如何选择物品装入背包，使得背包的总价值最大，且不超过背包容量。

动态规划解法：

1. 定义子问题： 对于背包容量为 c ，前 i 个物品，求装入背包的最大总价值。
2. 建立状态： 状态 dp[i][c] 表示背包容量为 c ，前 i 个物品装入背包的最大总价值。
3. 确定状态转移方程：
4. 如果物品 i 的重量大于背包容量 c ， dp[i][c] = dp[i-1][c]
5. 否则， dp[i][c] = max(dp[i-1][c], dp[i-1][c - weight[i]] + value[i])
6. 初始化： dp[0][0] = 0
7. 递推： 从 dp[1][1] 开始，依次计算每个 dp[i][c] 。
8. 回溯： 从 dp[n][c] 开始，通过状态转移方程回溯，得到装入背包的物品集合。

6.2.3 最短路径问题

问题描述： 给定一个带权有向图，求从起点到终点的最短路径。

动态规划解法：

1. 定义子问题： 对于起点 s 到图中任意节点 v ，求最短路径的权重。
2. 建立状态： 状态 dp[v] 表示从起点 s 到节点 v 的最短路径的权重。
3. 确定状态转移方程：
4. 如果存在从节点 u 到节点 v 的边，权重为 w ，则 dp[v] = min(dp[v], dp[u] + w)
5. 初始化： dp[s] = 0 ，其他节点 dp[v] = ∞
6. 递推： 从起点 s 开始，依次更新每个节点 v 的最短路径权重。
7. 回溯： 从终点 t 开始，通过状态转移方程回溯，得到最短路径。

7. 贪心算法

7.1 贪心算法的基本思想

贪心算法是一种在每一步都做出局部最优选择，从而得到全局最优解的算法。其基本思想是：

• 将问题分解成一系列子问题。
• 在每个子问题中，做出局部最优选择。
• 将局部最优选择组合起来，得到全局最优解。

7.2 贪心算法的应用

7.2.1 活动选择问题

问题描述：

给定一组活动，每个活动都有一个开始时间和结束时间，求出最多能参加的活动数量。

贪心算法：

1. 将活动按结束时间从小到大排序。
2. 选择第一个活动。
3. 从剩余活动中，选择第一个开始时间大于或等于当前活动结束时间的活动。
4. 重复步骤 3，直到没有剩余活动。

def activity_selection(activities):
    # 按结束时间排序
    activities.sort(key=lambda x: x[1])

    # 初始化已选择的活动
    selected_activities = [activities[0]]

    # 遍历剩余活动
    for i in range(1, len(activities)):
        # 如果当前活动开始时间大于或等于已选活动结束时间
        if activities[i][0] >= selected_activities[-1][1]:
            # 选择当前活动
            selected_activities.append(activities[i])

    # 返回已选活动数量
    return len(selected_activities)

7.2.2 哈夫曼编码

问题描述：

给定一组字符及其出现的频率，设计一种编码方案，使得编码后的字符串长度最短。

贪心算法：

1. 将字符按频率从小到大排序。
2. 选择频率最小的两个字符。
3. 创建一个新的字符，其频率为两个字符频率之和。
4. 将新字符添加到字符列表中。
5. 重复步骤 2-4，直到只有一个字符。
6. 每个字符的编码为从根节点到该字符的路径上所有字符的 0 和 1。

def huffman_encoding(frequencies):
    # 创建哈夫曼树
    while len(frequencies) > 1:
        # 选择频率最小的两个字符
        c1, c2 = min(frequencies, key=frequencies.get), min(frequencies, key=frequencies.get, key=lambda x: x != c1)

        # 创建新字符
        new_char = (c1, c2)
        new_freq = frequencies[c1] + frequencies[c2]

        # 更新频率表
        del frequencies[c1]
        del frequencies[c2]
        frequencies[new_char] = new_freq

    # 创建编码表
    encoding_table = {}
    def traverse(node, code):
        if isinstance(node, str):
            encoding_table[node] = code
        else:
            traverse(node[0], code + '0')
            traverse(node[1], code + '1')

    traverse(list(frequencies.keys())[0], '')

    # 返回编码表
    return encoding_table

7.2.3 最小生成树

问题描述：

给定一个连通无向图，求出一棵连接所有顶点的生成树，使得所有边的权重之和最小。

贪心算法：

1. 选择权重最小的边。
2. 将该边添加到生成树中。
3. 从生成树中删除所有与该边形成环的边。
4. 重复步骤 1-3，直到所有顶点都连接到生成树中。

def minimum_spanning_tree(graph):
    # 初始化生成树
    mst = []

    # 初始化边集
    edges = []
    for u in graph:
        for v in graph[u]:
            if u < v:
                edges.append((u, v, graph[u][v]))

    # 按权重排序
    edges.sort(key=lambda x: x[2])

    # 初始化并查集
    parent = [i for i in range(len(graph))]
    def find(x):
        if parent[x] != x:
            parent[x] = find(parent[x])
        return parent[x]

    # 遍历边集
    for u, v, w in edges:
        # 如果 u 和 v 不在同一个连通分量
        if find(u) != find(v):
            # 添加边到生成树
            mst.append((u, v, w))

            # 合并 u 和 v 所在的连通分量
            parent[find(u)] = find(v)

    # 返回生成树
    return mst

本文还有配套的精品资源，点击获取

简介：《算法导论》是计算机科学领域的经典教材，由麻省理工学院（MIT）的知名教授们合著。本课程设计项目经过测试，旨在帮助学生掌握算法设计、分析和实现的广泛主题。通过实践任务，学生将深入理解算法的核心概念，提升解决复杂问题的能力。本项目涵盖了排序与搜索算法、数据结构、分治策略、动态规划、贪心算法、回溯法、分支限界法、图论算法、递归与分形、概率算法、算法设计技巧和计算复杂性理论等关键知识点，为学生在算法领域的学习和应用打下坚实基础。

本文还有配套的精品资源，点击获取