这篇是写给我自己看的,一边记录一边在查阅想明白,感觉是很简单的事情,代码实现只有两行,但是存在两个疑惑:
- 为什么我步骤5得到的结果和直接使用PCA函数得到的结果不一样呢?
- 如果使用PCA函数,怎么知道舍弃了哪些特征,又保留了哪些特征?
希望知道答案的小伙伴可以在评论区回复。
特征的提取往往也是特征的筛选过程之一,遇到高维数据,可以通过PCA主成分分析方法和LDA线性判别分析两种方法来降低数据处理的维度,方便计算,这个过程也被叫做降维。
区别
- PCA:非监督降维(即没有标签),降维时选择方差尽可能大的数据作为特征(方差大,含有的信息量就大)
- LDA:有监督降维(即打好标签),降维后,组内(同一类别)方差小,组间(不同类别之间)方差大——》主要用于分类问题
PCA主成分分析
主成分分析法(PCA)的作用是:告诉我们在多维数据中,哪些变量对数据聚类最有价值,也就是以哪些变量为衡量标准可以更好地将数据点们区别开来。
如果对详细的工作原理和计算流程感兴趣,建议观看这个视频。
下面介绍一下计算步骤:
PCA适用对象的数据集维度一般都是2维以上(1维也用不上哈)
步骤1. 对每个维度进行中心化:同一属性求平均值mean,并用xi-mean,得到一个每个属性的均值都是0的新数据集。
| 样本1 | 样本2 | 样本3 | 样本4 | 样本5 | 样本6 | |
|---|---|---|---|---|---|---|
| 语文(x1) | 90 | 80 | 70 | 85 | 65 | 90 |
| 数学(x2) | 46 | 45 | 43 | 41 | 50 | 55 |
| 英语(x3) | 70 | 80 | 85 | 75 | 78 | 71 |
x1(mean)=(90+80+70+85+65+90)/6=80
x2(mean)=(46+45+43+41+50+55)/6=45
x3(mean)=(70+80+85+75+78+71)/6=76.5
将各行的每一项减去对应行的均值得到中心化后的数据:
| 新表格 | 样本1 | 样本2 | 样本3 | 样本4 | 样本5 | 样本6 |
|---|---|---|---|---|---|---|
| 语文(x1) | 10 | 0 | -10 | 5 | -15 | 10 |
| 数学(x2) | 1 | 0 | -2 | -4 | 5 | 10 |
| 英语(x3) | -6.5 | 3.5 | 9.5 | -1.5 | 1.5 | -5.5 |
接下来就只需要使用新表格里的数
步骤2.求解新表格的协方差
可以使用python计算:
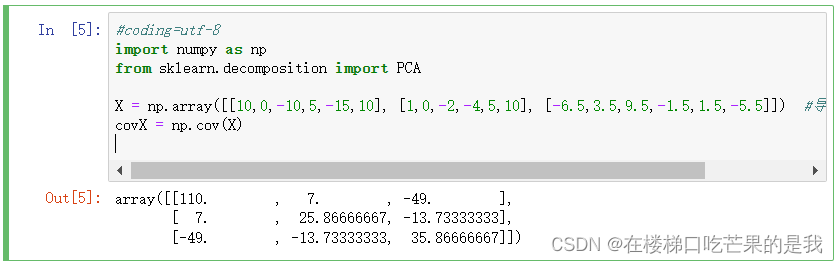
矩阵各值分别为:
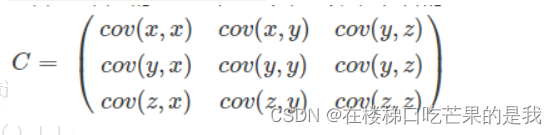
根据矩阵性质cov(x,y)=cov(y,x);可知x1,x2,x3三个变量间俩俩的协方差以推导出相关性:
- 当cov(X,Y)>0时,表示X与Y正相关;
- 当cov(X,Y)<0时,代表X与Y负相关;
- 当cov(X,Y)=0时,代表X与Y不相关。
步骤3.计算协方差矩阵的特征值和特征向量
可以使用python计算:
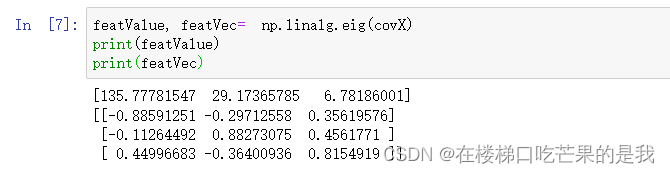
步骤4.特征值从大到小排序,并选择2个最大的特征值与对应的特征向量(前两行)
步骤5.将原矩阵乘上有2个特征向量的矩阵,得到降维的矩阵
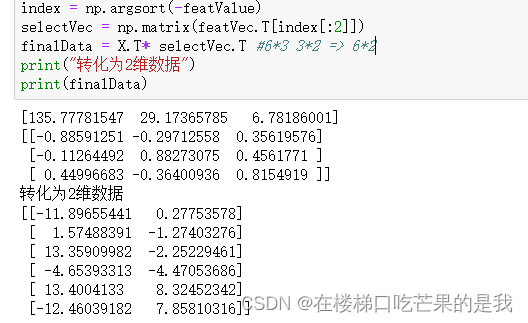
根据特征值,我们应该选择语文和数学成绩作为特征。
现在python里有封装好的代码,参数说明可看这篇:
#coding=utf-8
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[10,0,-10,5,-15,10], [1,0,-2,-4,5,10], [-6.5,3.5,9.5,-1.5,1.5,-5.5]])
X=X.T #导入数据,维度为3
pca = PCA(n_components=2) #降到2维
pca.fit(X) #训练
newX=pca.fit_transform(X) #降维后的数据
print(pca.explained_variance_ratio_) #输出贡献率
print(newX) #输出降维后的数据
[[-11.78380736 -1.13301391]
[ 1.68763097 -2.68458245]
[ 13.47184688 -3.66284429]
[ -4.54118608 -5.88108655]
[ 13.51316036 6.91397373]
[-12.34764476 6.44755347]]





















 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








