Protege实例【欧式几何五大公理】

0.目的

9月入门学习了protege，打算用protege做一个描述公理的推理demo，选定了实现欧式几何五大公理。
github连接放在这里了。

1. 过相异两点，能作且只能作一直线（直线公理）；
2. 线段（有限直线）可以任意地延长；
3. 以任一点为圆心、任意长为半径，可作一圆（圆公理）；
4. 凡是直角都相等（角公理）；
5. 两直线被第三条直线所截，如果同侧两内角和小于两个直角，则两直线则会在该侧相交。

描述公理相比较单纯表述人物关系会稍加难一些，可以观察到，如果仅仅是利用protege中的class类、individuals实例以及properties属性是难以表达这个复杂规则的。而在知识推理中，先验知识很多是以规则、定理、公理出现的，所以我们也需要掌握如何去描述复杂规则。

1.了解SWRL语言

SWRL：一种结合OWL和RuleML的语义Web规则语言，附上官网说明。

SWRL的表达逻辑是：前部的条件满足了——》后部的结果就会成立。
基于此的语法结构也很简单：条件1(？变量1)^条件2(？变量2,?变量3)->结论(?变量4)
例子1.1：如果角t1是直角，角t2也是直角-》则它们角度相同
直角(？t1)^直角(？t2)->相等(?t1,?t2)

需要注意的是：

1. 描述规则使用的不是类，而是实例。如例1.1所示，我们想说明任意两个直角都相等，并不用定义【任意】这个程度描述词，而是表示成“一个实例”，这个定义就已经包含了【任意】的意思。
2. 在描述规则时我们要尽可能将规则拆分成多个原子概念，例如直线公理中我们要拆出来“直线”、“点”等原子概念，以及“经过”、“相异”这样的原子关系。

那么在protege中要怎么描述类和关系呢？以下为官网地说明：

这些规则中的原子可以是C（x），P（x，y），sameAs（x，y）或differentFrom（x，y），其中C是OWL描述，P是OWL属性和x，y是OWL个体或OWL数据值等变量。请注意，连词规则使前因可以很容易地转换为多个规则，每个规则都有一个原子结果。

简单来说，想说明一个实例是某个类，就是可以【类名（？实例1）】；描述两个实例间的关系就可以是【关系名（？实例1，？实例2）】，这个关系就是三元组中的（实例1，关系，实例2），也是有向箭头，在表达是要注意顺序。
例如1.2：
规则：大黄是小黄的父亲-》大黄是爸爸
SWRL：父子（？x1，？x2）->爸爸(?x1)
现实：创建实例 大黄和小黄，描述关系父子（？大黄，？小黄），就可以推理出大黄是爸爸。

那么现在我们已经掌握了SWRL的基本运用方法，现在可以来尝试构建规则了。

2.使用SWRL描述欧式几何五大公理

刚刚提到，公理直接描述是很困难的，更何况几何公理许多都是建立在图形视觉方面，所以我们需要将公理进行一定的处理。如何处理，我并没有找到什么理论支持去规范，只能说各凭本事了，但是在转化的时候要确保两件事：

1. 正确性：转化后的内容是要符合语义，不能有偏颇：例如“过相异两点，能作且只能作一直线”可以转化成“直线1经过点1和点2，直线2也经过点1和点2，且点1和点2不同-》直线1=直线2
   ”，这样既说明了相异两点，有说明了直线的“唯一性”。
2. 完整性：转化后的内容要能完整表达，一条规则不够，可以多条规则说明一个定理。例如“以任一点为圆心、任意长为半径，可作一圆（圆公理）”，这里如果只说到了圆的唯一性，就缺少了圆心、半径的概念。

在此之前，没有使用过protege的伙伴可以以下两个教程，任意选择一个观看，知道如何添加class\individuals\properties就可以了。
基础教程1 和 基础教程2
切记！！！！做的过程中一定要随时保存文件，如果卡住或者不小心关闭，你做的东西就都没有啦！！！

2.0 准备工作

首先我们要备好SWRL：

接着我跟据5个公理创建好了类、关系和实例。注意在编写规则的过程中你可以随时修改、增添，所以不用太紧张。但是你需要事先有一个大概的、全局的考虑，例如什么概念是属性，什么概念是类。我写这个例子的目的是为了分享给大家做这件事的思路，这个例子本身没有什么意义，也不用追求和我的一模一样。
定义类：

直线的定义，同理可以写出线段的定义：
直角的定义，同理可以写出锐角和钝角（不过这里没用上）：
定义的关系属性：
数量属性：

2.1 公理一（详写）

• 找到自己要描述的规则，然后构思如何拆分成原子概念，定义好类、关系
• 使用SWRL语言将其表达出来
• 创建实例，检查是否可行

2.1.1 新建规则

公理：过相异两点，能作且只能作一直线（直线公理）；
转述：直线1经过点1和点2，直线2也经过点1和点2，且点1和点2不同-》直线1=直线2
swrl：math:点(?d1) ^ math:点(?d2) ^ math:不同于(?d1, ?d2) ^ math:直线(?x2) ^ math:直线(?x1) ^ math:线经过点(?x1, ?d2) ^ math:线经过点(?x1, ?d1) ^ math:线经过点(?x2, ?d2) ^ math:线经过点(?x2, ?d1) -> math:相同(?x1, ?x2)


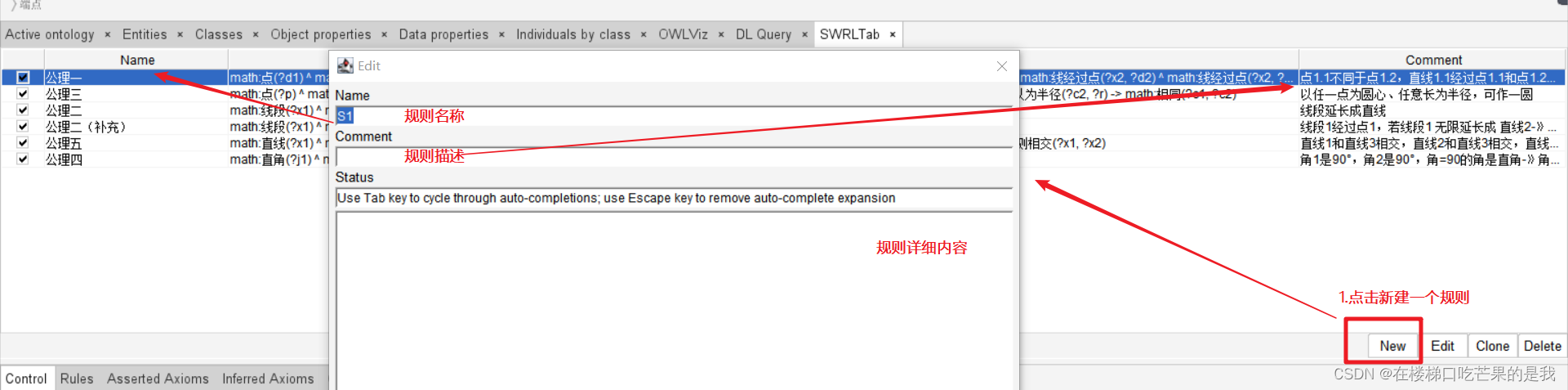
点击ok就完成了规则的添加。

2.1.2常见的错误

1.后果中用到的变量名，需要在前因中定义过。

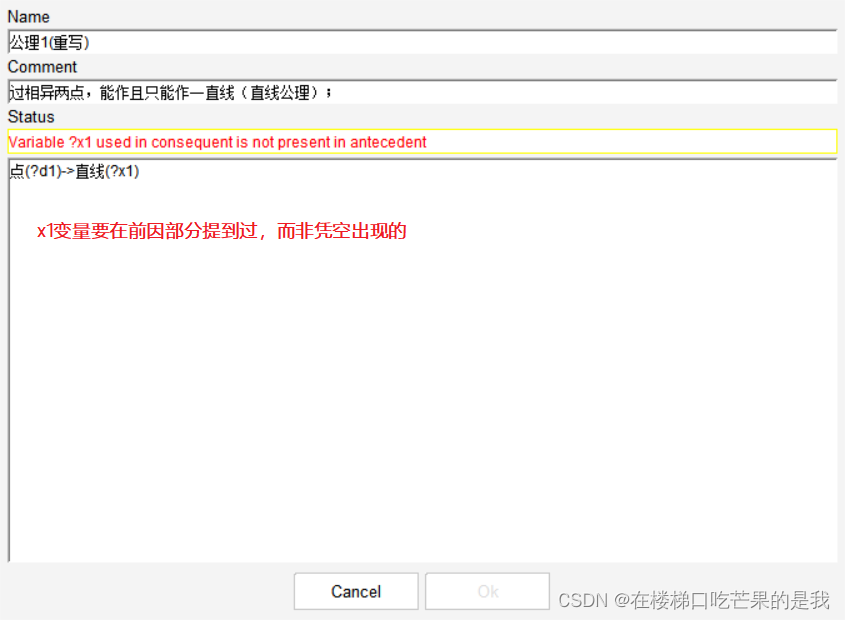
2.括号中的变量名前需要加？问号。

3.一个实例对应一次类的定义。

2.1.3 创建实例，检验规则

直线1.1【线经过点】点1.1
直线1.1【线经过点】点1.2
直线1.2【线经过点】点1.1
直线1.2【线经过点】点1.2
点1.1【不同于】点1.2
符合规则的前部条件，则得到推理结果（右下角黄色部分）——直线1.1与直线1.2相同。

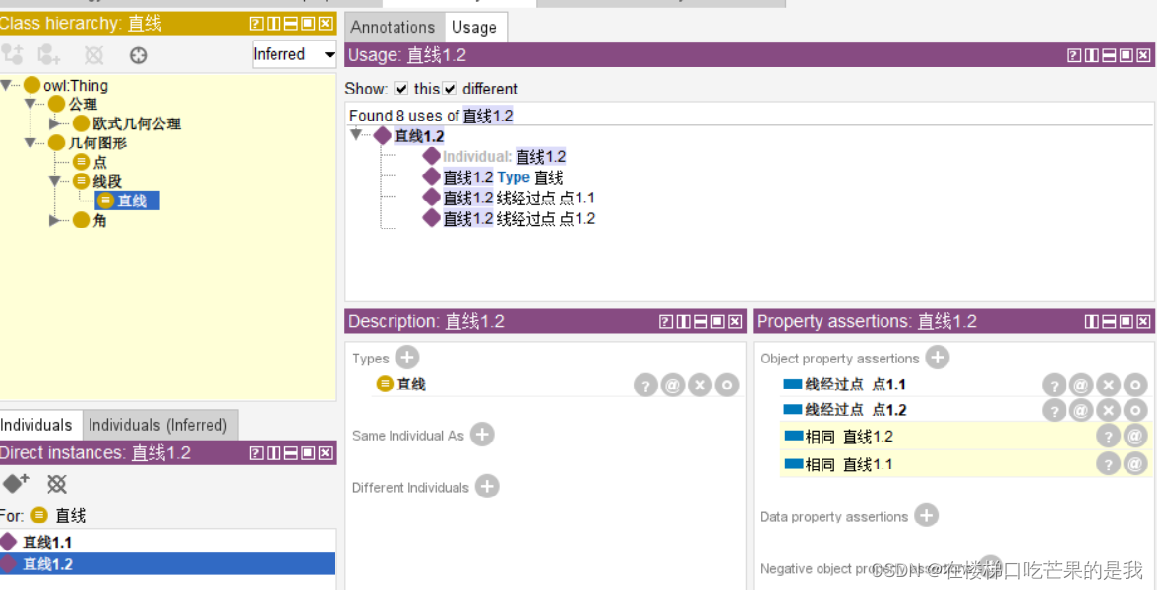
点开推理结果的问号部分，可以看的protege提供的推理思路，可以看到我们自己编写的规则起作用了，说明可行。
之后再将剩余四个公理完成即可。

2.2 公理二

公理：线段（有限直线）可以任意地延长；
转述：线段1无限延长成x2-》x2为直线
线段1经过点1，点2，若线段1 无限延长成 直线2，-》直线2经过点1，点2（说明两点确定一条唯一的线段）
swrl：math:线段(?x1) ^ math:点(?d1) ^ math:线经过点(?x1, ?d1) ^ math:无限延长成(?x1, ?x2) -> math:线经过点(?x2, ?d1)

2.3 公理三

公理：以任一点为圆心、任意长为半径，可作一圆（圆公理）；
转述：两个圆的圆心（位置一样）和半径（长度一样）是一致的，那么两个圆完全一样
swrl：math:点(?p) ^ math:线段(?r) ^ math:圆(?c1) ^ math:圆(?c2) ^ math:以为圆心(?c1, ?p) ^ math:以为半径(?c1, ?r) ^ math:以为圆心(?c2, ?p) ^ math:以为半径(?c2, ?r) -> math:相同(?c1, ?c2)

2.4 公理四

公理：凡是直角都相等（角公理）；
转述：角1是90°，角2是90°，角=90的角是直角-》角1=角2
swrl：math:直角(?j1) ^ math:直角(?j2) -> math:等于(?j1, ?j2)

2.5 公理五

公理：两直线被第三条直线所截，如果同侧两内角和小于两个直角，则两直线则会在该侧相交。
转述：直线1和直线3相交，直线2和直线3相交，直线1和直线2同侧两内角和小于两个直角-》直线1和直线2相交（同侧）
swrl：math:直线(?x1) ^ math:直线(?x2) ^ math:直线(?x3) ^ math:相交(?x1, ?x3) ^ math:相交(?x2, ?x3) ^ math:同侧2内角和小于180(?x1, ?x2) -> math:同侧相交(?x1, ?x2)

好啦，以上就是我的学习笔记。
可以看到还有很多不足，例如公理五没有彻底原子化，应当进一步去把线相交成角的概念去规范和细化，同侧角的定义去明确……
我也会在之后的学习中去反思这些问题。