三个点在同一个半圆的概率_11588 一道「小黄鸭」概率题及其有趣扩展 (3)

　　（题图来自：如果洗澡时你的壁纸冲了进来，你会怎么办？）

　　在这一篇中，我们来直捣黄龙地研究如下问题：在

维空间中的

维超球面上随机、均匀地选取

个点，它们位于同一个半超球面的概率是多少？

　　在本系列的第 2 篇中，我们借助「

维单纯形」的概念从低维突破进了高维，但这带来了「点数必须等于空间维数加 1」的局限。要打破这个局限，就只能扔掉「单纯形」这根拐棍了。既然问题是关于「半超球面」的，我们就从这个概念本身入手。

　　注意到，在「半超球面」上，有一个「极点」的概念。例如，在三维空间中，考虑地球的表面，那么「北半球」这个半球面的极点就是「北极」。反过来，在超球面上，指定一个极点，也能唯一确定一个半超球面。仍以地球为例，指定「南极」这个极点后，就唯一确定了「南半球」这个半球面。这样，我们就把「半超球面」这种庞然大物，跟「点」这种小巧玲珑的概念对应了起来。我们可以考虑：若

个点位于同一个半超球面上，那么这个半超球面的极点 P，要满足什么条件呢？

　　我们回到二维来直观地观察。设二维空间中有一个圆 O，其圆周上有 A、B、C 三点位于同一个半圆弧上，这个半圆弧的极点为 P。不难发现，角 POA、POB、POC 都必须是锐角（或直角）。

图 3.1：A、B、C 三点都位于以 P 为极点的半圆弧上

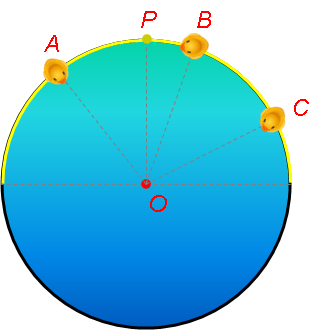
　　注意，在「角 POA」这个说法中，点 P 和点 A 的地位是对称的。这提示我们，「A 位于以 P 为极点的半圆弧上」，也可以说成是「P 位于以 A 为极点的半圆弧上」。于是我们就发现了点 P 可以活动的范围：它必须位于以 A、B、C 为极点的三个半圆弧的交集中。如果像下图（左）那样，这三个半圆弧有交集（黄色圆弧），那么就可以说「A、B、C 位于同一个半圆弧上」，P 点可以在这个交集里自由活动；如果像下图（右）那样，这三个半圆弧没有交集，那么 A、B、C 三点就不位于同一个半圆弧上，P 点就无处容身了。

图 3.2：（左）P 点位于以 A、B、C 为极点的三个半圆弧的交集（黄色圆弧）上；（右）以 A、B、C 为极点的三个半圆弧没有交集，P 点不存在

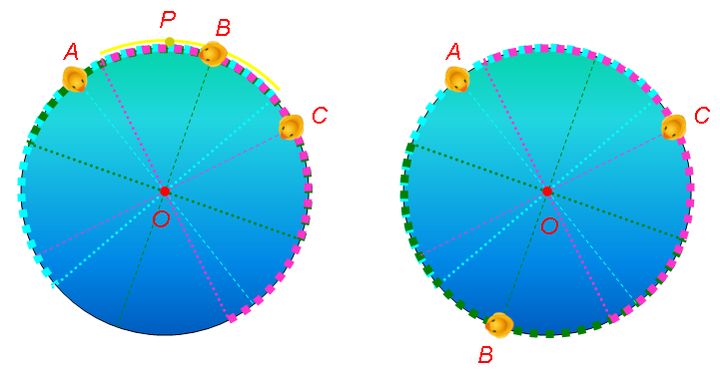
　　在上面的两个图里，我把 B 点画在了同一条直径的两端。这有没有让你想到些什么呢？对！我们还可以借鉴上一篇中「把取点的过程拆开描述」的办法，让最后一步是「在直径上等可能选取端点」。在上一篇中，C 点的地位是与 A、B 不同的，所以单独用了一步来描述它。而现在，A、B、C 的地位都是相同的，所以只需要用两步来描述取点的过程：

　　1. 随机、均匀地选取三条直径；
　　2. 在每条直径上，分别等可能地选取一个端点作为 A、B、C。

　　选定直径后，第 2 步「选取端点」有 8 种取法。上面的图 3.2 画出了其中的两种；把 8 种全部画出来太麻烦了，我就省略了。重要的问题是：在这 8 种取法中，有几种会使得以 A、B、C 为极点的半圆弧有交集呢？

　　观察图 3.2 中以 B 为极点的半圆弧。与 OB 垂直的直径把圆周切成了两半，以 B 为极点的半圆弧必为其中的一半。同样，以 A、C 为极点的半圆弧，也必然是与 OA、OC 垂直的直径把圆周切成的两半中的一半。把多余的线都擦掉，只保留与 OA、OB、OC 垂直的三条直径，如下面的图 3.3。可以看到，它们把圆周切成了 6 份。其中的每一份，都是三个半圆弧的交集，也就对应着「选取端点」的一种方法。注意这与 6 份的大小无关！

图 3.3：与 OA、OB、OC 垂直的三条直径，把圆周分成了 6 份

　　于是得到：在 8 种选取端点的方法中，有 6 种可以使得以 A、B、C 为极点的三个半圆弧有交集。这 8 种选法是等可能的，所以 A、B、C 位于同一半圆弧上的概率为

。这是一个常数，所以可以免去对第 1 步求期望的步骤，

就是最终答案。

　　上面研究的是二维空间中 3 个点的情况。首先我们对点数进行推广。当点数为

时，在

条直径中选取端点有

种取法。与这些直径垂直的那些直径，会把圆周分割成

份，其中每一份对应着一种能使所有点都位于同一个半圆弧上的取法。所以

个点位于同一半圆弧上的概率就是

。你看，我们得到了与第 1 篇中相同的结论！

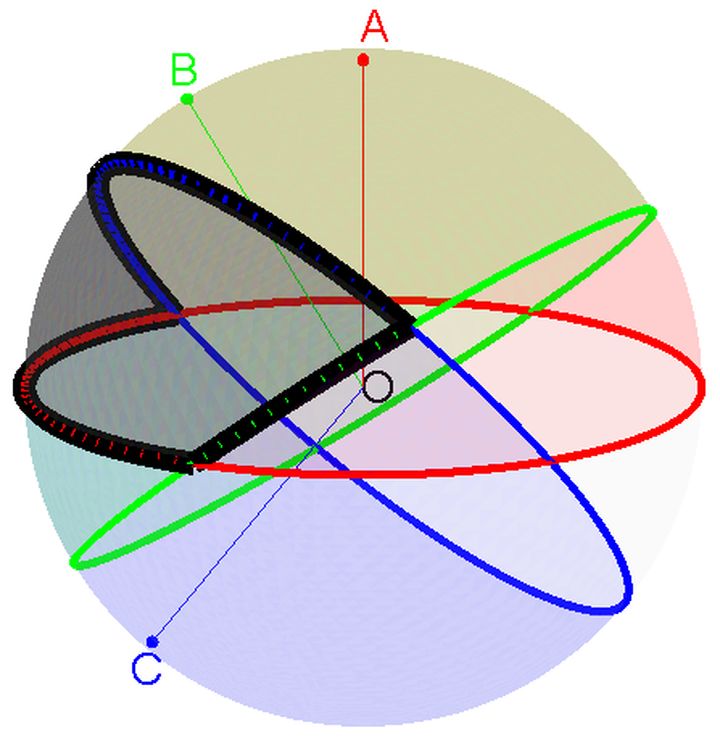
　　下面我们往高维推广。为了避免步子太大扯到蛋，我们先看三维情况。若在球面上选取三个点 A、B、C，则它们位于同一个半球面的充要条件是，以 A、B、C 为极点的三个半球面有交集。如图 3.4 所示，以 A、B、C 为极点的三个半球面的交集是黑色区域。在此区域内任取一点为极点，作一个半球面，都能把 A、B、C 三点包含在内。

图 3.4：以 A、B、C 为极点的三个半球面有交集（黑色区域）

　　仍考虑「两步取点法」：

　　1. 随机、均匀地选取三条直径；
　　2. 在每条直径上，分别等可能地选取一个端点作为 A、B、C。

　　第 2 步有 8 种取法，其中有几种能使得三个半球面有交集呢？以 A 为极点的半球面，是与 OA 垂直的大圆面（图 3.4 中的红色圆圈所在的平面）把球面切成两半后的一半。注意，切割球面的是大圆面，不是直径了！与 OA、OB、OC 分别垂直的三个大圆面（图 3.4 中红、绿、蓝三个圆圈所在平面）把球面切成的每一块，就对应着一种能使得三个半球面有交集的取法。三个大圆面会把球面切成 8 块（不考虑特殊情况），所以球面上的三个点位于同一个半球面的概率为

。

　　咦？这个概率怎么等于 1 了？没有错吗？确实没错。三点定一面，过球心作一个平面 F 与此面平行，则三点都在平面 F 的同侧，当然位于同一个半球面啦。

　　对点数推广：在三维空间里的球面上随机、均匀地选取

个点，它们位于同一个半球面的概率是多少呢？根据刚才的经验，这个概率应该是一个分数，它的分母等于

，而分子是

个大圆面把球面切成的块数。且慢，我先数一下 4 个大圆面把球面切成的块数：

图 3.5：4 个大圆面把球面切成了几块呢？

　　好像有点数不清了呢……

　　更一般地，在

维空间里的

维超球面上随机、均匀地选取

个点，它们位于同一个半超球面的概率也是一个分数，其分母等于

，而分子是

个过超球心的

维超平面把超球面切成的块数。天啊，这怎么数……

　　且听下回分解。

---

　　本系列共有 5 篇文章，以下是传送门：(1) (2) (3) (4) (5)