左右 映射_MIT—线性代数笔记33 左右逆和伪逆

第33讲 左右逆和伪逆

Left and right inverses; pseudoinverse

网易公开课​open.163.com

本节主要介绍左右逆矩阵和伪逆矩阵。

• 两侧逆矩阵 2-sided inverse

矩阵A的两侧逆矩阵

满足

。这就是我们通常说矩阵

A的逆矩阵。此时r=m=n， A为满秩方阵。

• 左逆矩阵 Left inverse

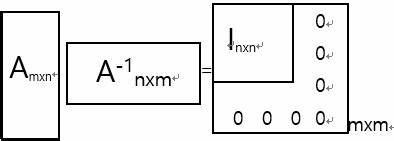
矩阵A的列满秩r=n，列向量线性无关。则矩阵的零空间N(A)只有零向量，方程Ax=b无解或者有唯一解。当矩阵A列满秩的时候，矩阵

为可逆矩阵，这是讨论最小二乘问题的核心。

矩阵

为nxn的对称矩阵且满秩，因此矩阵

是可逆矩阵，即

。我们称

为

A的左逆矩阵。

为nxm矩阵，而

A为mxn矩阵，

是nxn矩阵。

• 右逆矩阵 Right inverse

矩阵A的行满秩r=m，行向量线性无关。则矩阵的左零空间N(

)只有零向量。

A的零空间维数为n-m，因此有n-m个自由变量，n大于m时，方程 Ax= b有无穷多解。

矩阵A的右逆矩阵为

。

通常情况下右乘左逆矩阵得不到单位阵，

，这是列空间的投影矩阵。仅在m=n的条件下，

。一个长方形矩阵

A不可能有两侧逆，因为 A和

总有一个零空间的维数不是0。

同样的，左乘右逆矩阵得到的是

，这是向行空间投影的矩阵，投影矩阵在投影空间内表现的就像单位阵

I一样。

• 伪逆矩阵Pseudoinverse

可逆矩阵的零空间和左零空间只有零向量。列满秩的矩阵的零空间只有零向量，行满秩的矩阵的左零空间只有零向量。但对于不满秩的矩阵（r<n，r<m），其两个零空间均存在，这就使得它取不到逆矩阵。

因为逆矩阵的作用可以看作是原矩阵的逆操作，但是矩阵 A对其零空间中向量操作后变为 0，这时没有逆操作能够恢复这一过程，所以带有零空间就不能取逆矩阵。

观察不满秩矩阵A的四个子空间，其行空间和列空间的维数相等，均为r。在其行空间中的向量x经过矩阵A操作后，变为列空间中的向量Ax。而x与Ax为一一对应的关系。如果将矩阵A限制在行空间和列空间上，它是个可逆矩阵，此时A的逆矩阵就是所谓的“伪逆矩阵

”。

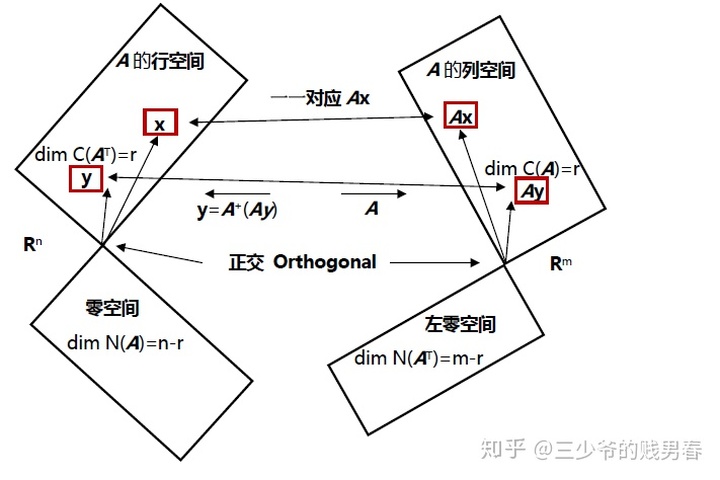
问题的关键就是一一对应，即对于行空间中的向量x≠y，其通过矩阵A映射到列空间得到的向量Ax≠Ay。

证明：若行空间中存在向量y与向量x在列空间中对应的向量相同，则有Ax-Ay=0，即A(x-y)=0，则x-y为矩阵A零空间中的向量，但矩阵的行空间对线性运算封闭，因此x-y为行空间中的向量，因两个子空间正交，所以有(x-y)=0，即x与y相同。因此行空间与列空间中的向量为一一对应。

统计学家非常需要伪逆矩阵，因为他们要做很多最小二乘法进行线性回归的问题。如果矩阵不满秩，则矩阵

为不可逆，所以无法用之前的办法解决，此时要用到伪逆矩阵。

求伪逆矩阵

的一个方法是利用奇异值分解

，其中对角阵

是由矩阵奇异值排列在对角线上构成的mxn矩阵，其秩为r。则伪逆矩阵

为nxm矩阵，矩阵的秩也为r。

，

，

,

矩阵右乘伪逆矩阵得到

是mxm矩阵，矩阵对角线前r个元素为1，其它元素均为0，而左乘伪逆矩阵

得到nxn，矩阵对角线前r个元素为1，其它元素均为0，这两个都是 的投影矩阵，一个投影到行空间，一个投影到列空间。

而矩阵A的伪逆矩阵为

。

---

逆矩阵满足四个性质：

注意：

得到的并不是形如

这种对角线上只有1和0的对角阵，所得结果是

A行空间的投影矩阵。
例如 A=

,通过奇异值分解计算可以得到

=

。而

AA+=

。