【图】图的相关基础知识

哒哒翔

已于 2023-05-17 14:15:48 修改

阅读量403

点赞数

文章标签：算法图论数据结构

于 2023-04-28 15:26:33 首次发布

本文链接：https://blog.csdn.net/weixin_42596089/article/details/130406195

版权

什么是图？

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。简言之，图是由节点以及它们之间的连线的集合，根据连线的不同又分为有向图和无向图。前面章节讲解中树结构的一个基本特点，是数据元素之间具有层次关系，每一层的元素可以和多个
下层元素关联，但是只能和一个上层元素关联。如果把这个规则进一步扩展，也就是说，每个数据
元素之间可以任意关联，这就构成了一个图结构。正是这种任意关联性，导致了图结构中数据关系
的复杂性。研究图结构的一个专门理论工具便是图论。
在这里插入图片描述

无向图相关概念

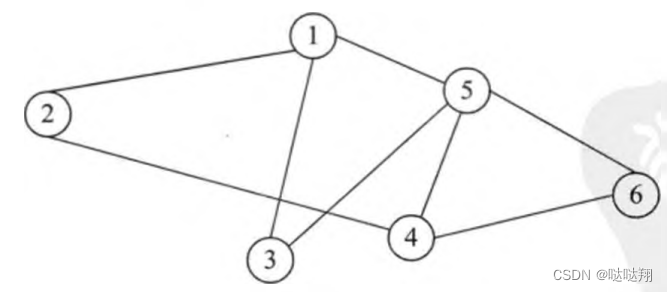
如果一个图结构中，所有的边都没有方向性，那么这种图便称为无向图。典型的无向图，由于无向图中的边没有方向性，这样，我们在表示边时对两个顶点的顺序没有要求。
例如顶点V1和顶点V5之间的边，可以表示为（V1，V5） , 也可以表示为（V5，V1）。
所示的无向图，对应的顶点集合和边集合如下：
V(G）= {V1,V2,V3,V4,V5}
E ( G ) = { ( V 1, V 2) ，（ V 1, ’V 5) ，（ V 2，V 4) , ( V 3, V 5) ， ( V 4 , V 5) , ( V1 , V 3)
在这里插入图片描述

有向图相关概念

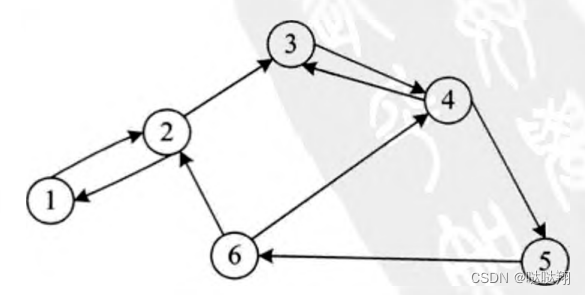
如果一个图结构中，边是有方向性的，那么这种图便称为有向图。典型的有向图，如图所示。由于有向图中的边有方向性，所以在表示边时一对两个顶点的顺序有所要求。并且，为了与无向图区分，这里采用尖括号表示有向边。例如，<V3，V4>表示从顶点V3到顶点V4的一条边，而<V4,V3>表示的是V4到顶点V3的一条边。< V3,V4>和<V4，V3>表示的是两条不同的边。
所示的有向图,对应的顶点集合和边集合如下：
V(G）= {V.,V2,V3,V4,V5,V6}
E(G）= {<V1,V2>,<V2,V1>,<V2,V3>,<V3,V4>,<V4,V3>,<V4,V5>,<V5,V6>,<V6,V4>,<V6,V2>}
在这里插入图片描述

顶点的度 Degree)

连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图，一个顶点V的度比较简单，其是连接该顶点的边的数量，记为D(V)。例如所示的无向图中，顶点V4的度为2 ，而 V5 的度为 3。
对于有向图要稍复杂些，根据连接顶点V的边的方向性，一个顶点的度有入度和出度之分。
• 入度是以该顶点为端点的入边数量，记为lD(V)。
• 出度是以该顶点为端点的出边数量，记为OD(V)。
这样，有向图中，一个顶点V的总度便是入度和出度之和，即 D(V)= ID(V)+OD(V)。例如所示的有向图中，顶点V3的入度为2 , 出度为1，因此，顶点V3的总度为3。
在这里插入图片描述

邻接顶点

邻接顶点是指图结构中一条边的两个顶点。邻接顶点在有向图和无向图中具有不同的表示。对于无向图，邻接顶点比较简单。例如所示的无向图中，顶点V1和顶点V5互为邻接顶点，
顶点V2和顶点V4互为邻接顶点等。另外，顶点V1的邻接顶点有顶点V2, 顶点V3和顶点V5。
对于有向图要稍复杂些，根据连接顶点V的边的方向性，两个顶点分别称为起始顶点（起点或始点）和结束顶点（终点）。有向图的邻接顶点分为两类。
• 入边邻接顶点：连接该顶点的边中的起始顶点。例如，对于组成<V1, V2>这条边的两个顶点，V1是V2的入边邻接顶点。
• 出边邻接顶点：连接该顶点的边中的结束顶点。例如，对于组成<V1, V2>这条边的两个顶点，V2是V1 的出边邻接顶点。

无向完全图

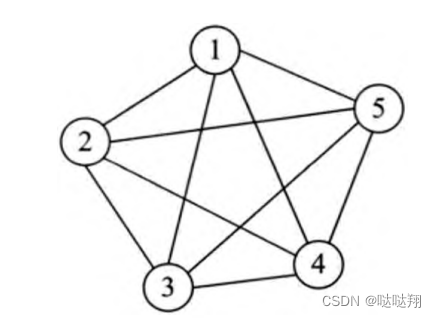
如果在一个无向图中，每两个顶点之间都存在一条边，那么这种图结构称为无向完全图。典型的无向完全图，如图所示。
从理论上可以证明，对于一个包含N的顶点的无向完全图，其总的边数为N(N-1)/2
在这里插入图片描述

有向完全图

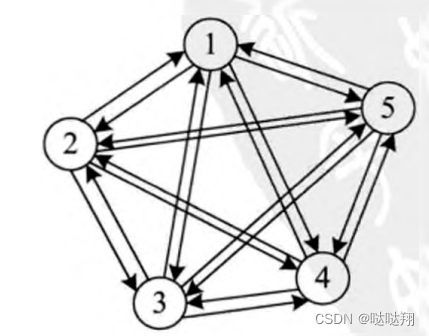
如果在一个有向图中，每两个顶点之间都存在方向相反的两条边，那么这种图结构称为有向完全图。典型的有向完全图，如图所示。
从理论上可以证明，对于一个包含N的顶点的有向完全图，其总的边数为N(N-1)。这是无向完全图的两倍，这个也很好理解，因为每两个顶点之间需要两条边。
在这里插入图片描述

子图

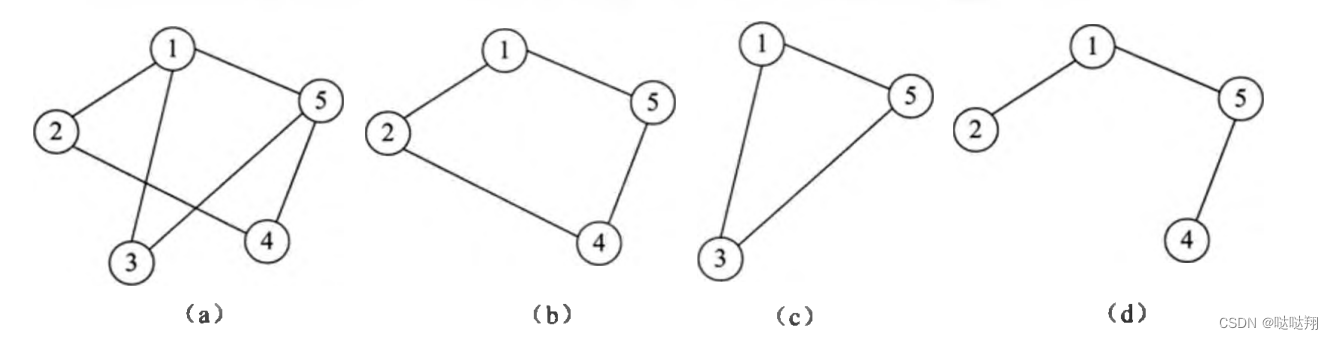
子图的概念类似于子集合，由于一个完整的图结构包括顶点和边，因此，一个子图的顶点和边都应该是另一个图结构的子集合。例如，图（a ) 为一个无向图结构，图（b )、图（c) 和图（d ) 均为图（a ) 的子图。
这里需要强调的是，只有顶点集合是子集的，或者只有边集合是子集的，都不是子图。
在这里插入图片描述

路径

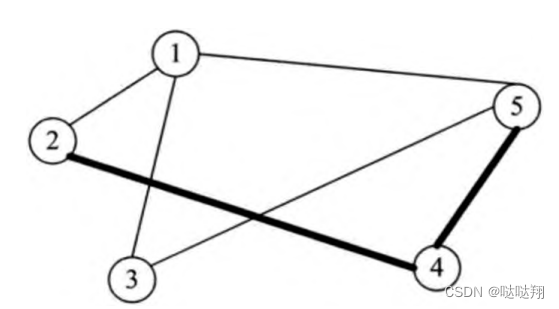
路径就是图结构中两个顶点之间的连线，路径上边的数量称之为路径长度。两个顶点之间的路径可能途经多个其他顶点，两个顶点之间的路径也可能不止一条，相应的路径长度可能不一样。典型的图结构中的路径，如图所示。粗线部分显示了顶点V5到V2之间的一条路径，这条路径途
经的顶点为V4, 途经的边依次为（V5, V4）、（V4，V2) , 路径长度为2。
在这里插入图片描述

同样，我们还可以在该图中找到顶点V5到V2之间的其他路径，分别为：
• 路径(V5, V1), (V1, V2)途经顶点V1, 路径长度为2 。
• 路径(V5, V3), (V3,V1). (V1,V2) , 途经顶点V1和V3, 路径长度为3。
图结构中的路径还可以细分为如下几种形式。
• 简单路径：在图结构中，如果一条路径上顶点不重复出现，则称之为简单路径。
• 环：在图结构中，如果路径的第一个顶点和最后一个顶点相同，则称之为环，有时也称之为回路。
• 简单回路：在图结构中，如果除第一个顶点和最后一个顶点相同外，其余各顶点都不重复的回路称为简单回路。

连通, 连通图和连通

通过路径的概念，可以进一步研究图结构的连通关系，主要涉及如下几点。
• 如果图结构中两个顶点之间有路径，则称这两个顶点是连通的。需要注意连通的两个顶点可
以不是邻接顶点，只要有路径连接即可，可以途经多个顶点。
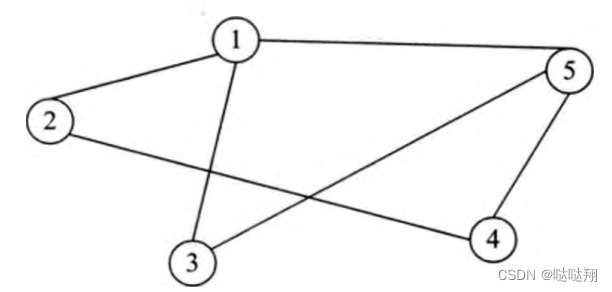
• 如果无向图中任意两个顶点都是连通的，那么这个图便称为连通图。如果无向图中包含两个
顶点是不连通的，那么这个图便称为非连通图。
• 无向图的极大连通子图称为该图的连通分量。
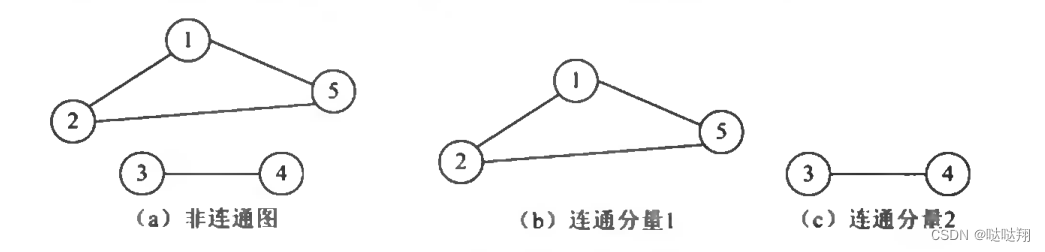
理论可以证明，对于一个连通图，其连通分量有且只有一个，就是该连通图自身。而对于一个非连
通图，则有可能存在多个连通分量。如图所示的图结构中，图（a ) 为一个非连通图，因为顶
点V2和顶点V3之间没有路径。这个非连通图中的连通分量包括两个，分别为图（b ) 和图（c )。
在这里插入图片描述

强连通图和强连通

与无向图类似，在有向图中也有连通的概念，主要涉及如下几个。
• 如果两个顶点之间有路径，也称这两个顶点是连通的。需要注意的是，有向图中边是有方向
的。因此，有时从Vi到 Vj连通的，但从Vj 到Vi却不一定连通。
• 如果有向图中任意两个顶点都是连通的，则称该图为强连通图。如果有向图中包含两个顶点
不是连通的，则称该图为非强连通图。
• 有向图的极大强连通子图称为该图的强连通分带。
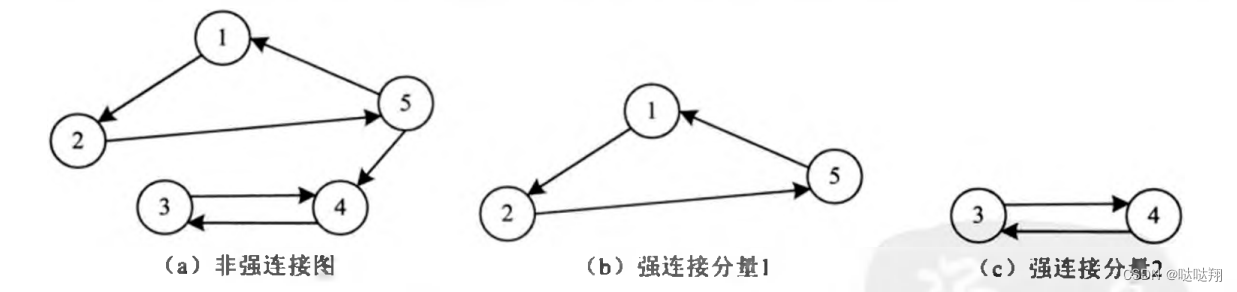
从理论上可以证明，强连通图只有一个强连通分量，那就是该图自身。而对于一个非强连通图，则
有可能存在多个强连通分量。如图所示的图结构中，图（a ) 为一个非强连通图，因为其中顶点V2和顶点V3之间没有路径。这个非强连通图中的强连通分量包括两个，分别为图（b ) 和图（c )。
在这里插入图片描述

权

前面介绍的图，各个边并没有赋予任何含义。在实际的应用中往往需要将边表示成某种数值，
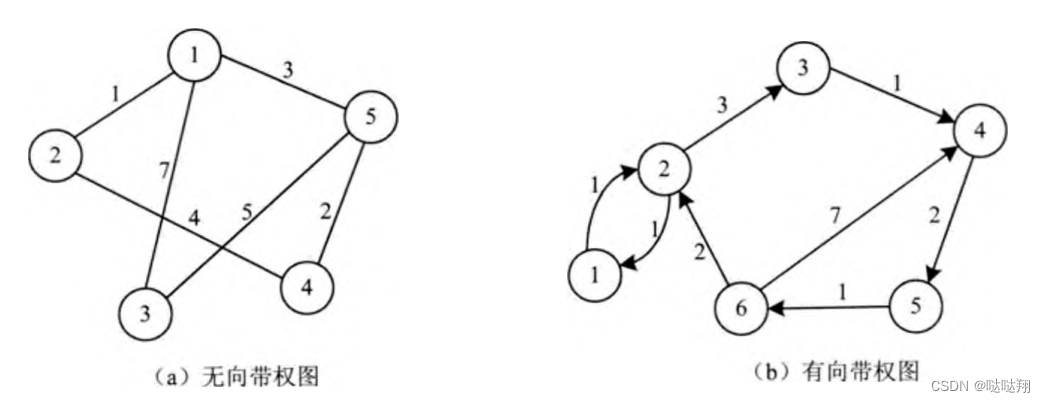
这个数值便是该边的权（W eight)。无向图中加入权值，则称之为无向带权图。有向图中加入权值，
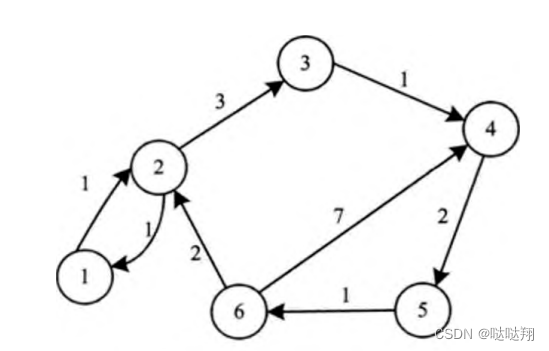
则称之为有向带权图。典型的无向带权图和有向带权图，如图所示。权在实际应用中可以代表各种含义，例如在交通图中表示道路的长度，在通信网络中表示基站之间的距离，在人际关系中代表亲密程度等。
在这里插入图片描述

设计图的准备结构，并准备数据

掌握前面的理论知识后，下面就开始图结构的程序设计。首先需要准备数据，也就是准备在图

结构操作中需要用到的变量及数据结构等。由于图是一种复杂的数据结构，顶点之间存在多对多的
关系，所以我们无法简单地将顶点映射到内存中。
在实际应用中，通常需要采用结构数组的形式来单独保存顶点信息，然后采用二维数组的形式
保存顶点之间的关系。这种保存顶点之间关系的数组称为邻接矩阵（Adjacency Matrix)。
这样，对于一个包含n个顶点的图，可以使用如下的语句来声明一个数组保存顶点信息，声明
一个邻接矩阵保存边的权：

char vertex[n];  //保存顶点信息（序号或字母）
int edgeweight[n][n]; //邻接矩阵，保存边的权

对于数组 Vertex，其中每一个数组元素保存顶点信息，可以是序号或者字母。而邻接矩阵
EdgeVeight保存边的权或者连接关系。
在表示连接关系时，该二维数组中的元素Edgeweight[i]j]=1表示Vi，Vj) 或<Vi，Vj>构成一条边，
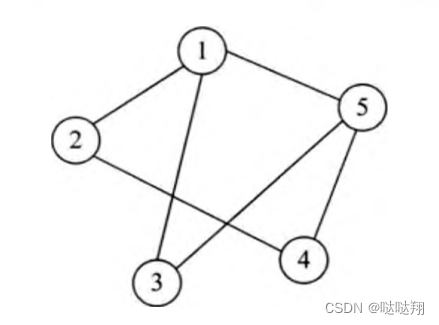
如果edgeweight[i][j]=0 表示或< Vi，Vj>不构成一条边。例如图所示的无向图，我
们可以采用一维数组来保存顶点，保存的形式如图。
在这里插入图片描述

实例代码：

vertex[1]=1;
vertex[2]=2;
vertex[3]=3;
vertex[4]=4;
vertex[5]=5;

对于邻接矩阵，我们可以按照图所示进行存储。对于有边的两个顶点，在对应的矩阵元素中填入1。例如，V1和V3之间存在一条边，因此edgeweight[1][3]中保存1 ,而V3和V1 之间存在一条边，因此edgeweight[3][1]中保存1。由此可见，对于无向图，其邻接矩阵左下角和右上角是对称的。

对于有向图，如图所示。保存顶点的一维数组形式不变，如图所示。而对于邻接矩阵，仍然采用二维数组，其保存形式如图所示。对于有边的两个顶点，在对应的矩阵元素中保存1。这里需要注意的是，边是有方向的。
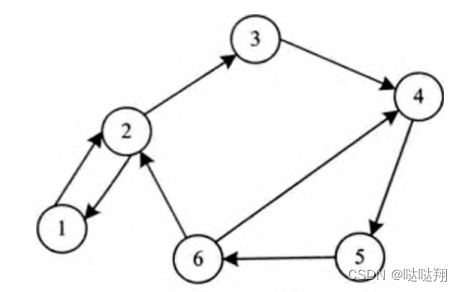
在这里插入图片描述
例如，顶点 V 2 到顶点 V 3 存在一条边，因此在EdgeVeight [2][3]中保存1，而顶点V3到顶点V2不存在边，因此在EdgeVeight [3][2]中保存0。对于带有权值的图来说，邻接矩阵中可以保存相应的权值。也就是说，此时，有边的项保存对应的权值，而无边的项则保存一个特殊的符号Z 。例如，对于图中所示的有向带权图，其对应的邻接矩阵的存储形式，如图所示。这里需要注意的是，在实际程序中为了保存带权值的图，往往定义一个最大值M A X , 其大于所有边的权值之
和，用 M A X 来替代特殊的符号Z 保存在二维数组中。
在这里插入图片描述

图结构操作示例：

#include <bits/stdc++.h>
using namespace std;
#define maxnum 20  //图的最大顶点数
#define maxvalue 65535  //最大值（可设为一个最大整数）

typedef struct {
	char vertex[maxnum];  //保存顶点信息（）序号或字母
	int Gtype;   //图的类型 （0：无向图，1，有向图）
	int vertexnum; //顶点的数量
	int edgenum; //边的数量
	int edgeweight[maxnum][maxnum]; //保存边的权值
	int istrav[maxnum];  //遍历标志
}Graphmatrix; //定义邻接矩阵图结构

//邻接矩阵是一种表示图的方法，它通过一个二维矩阵来描述图中各个顶点之间的关系。邻接矩阵有两种不同的实现方式：有向图和无向图。
//对于无向图，邻接矩阵的构建过程如下：
//1. 创建一个 n*n 的矩阵，其中 n 表示图中顶点的数量。
//2. 将矩阵中所有元素初始化为 0。
//3. 对于每条边 (i, j)，将矩阵中第 i 行第 j 列和第 j 行第 i 列的元素都设置为 1。
//4. 如果有权重，可以将矩阵中的 1 替换为相应的权重值。
//5. 对于有向图，邻接矩阵的构建过程与无向图基本相同，只是在设置矩阵元素时，只需将一个方向上的元素设为 1 即可。
//需要注意的是，邻接矩阵是一种稠密表示方法，适用于顶点数量较少，边数较多的图。对于稀疏图，使用邻接矩阵会造成大量空间浪费，建议使用邻接表等其他表示方法。
void createGraph(Graphmatrix *GM){  //创建邻接矩阵图
	int i,j,k;   
	int weight;  //权
	char EstartV,EendV;  //边的起始顶点
	
	for( i=0;i<GM->vertexnum;i++){  //输入顶点
		getchar();
		//getchar() 单独使用，它会等待用户输入一个字符，并返回该字符的 ASCII 码值。然后程序就会继续执行下面的语句。
		//但是由于没有将该字符存储在任何变量中，因此该字符将被丢弃，而不被程序使用。如果用户输入了多个字符，
		//则 getchar() 只会返回第一个字符的ASCII 码值，并丢弃其余的字符。在这种情况下，后续的 getchar() 调用将等待用户输入的下一个字符。
		scanf("%c",&(GM->vertex[i])); //保存到各顶点数组元素中
	}
	
	for(k=0;k<GM->edgenum;k++){  //输入边的信息
		getchar();
		scanf("%c %c %d", &EstartV, &EendV, &weight);
		for(i=0; EstartV!=GM->vertex[i];i++); //在已有顶点中查找始点
		for(j=0; EendV!=GM->vertex[j];j++);   //在已有顶点中查找终点
		GM->edgeweight[i][j]=weight;          //对应位置保存权值，表示有一条边
		if(GM->Gtype==0){                     //若是无向图
			GM->edgeweight[j][i]=weight;      //在对角位置保存权值
		}
	}
} 

void clearGraph(Graphmatrix *GM){
	int i,j;
	for(i=0;i<GM->vertexnum;i++){             //清空矩阵
		for(j=0;j<GM->vertexnum;j++){
			GM->edgeweight[i][j]=maxvalue ;   //设置矩阵中各元素的值为MaxValue
		}
	}
}

void outgraph(Graphmatrix *GM){  //输出邻接矩阵
	int i,j;
	for(j=0;j<GM->vertexnum;j++){
		printf("\t%c", GM->vertex[j]); //在第一行输出顶点信息
	}
	printf("\n");
	for(i=0;i<GM->vertexnum;i++){
		printf("%c",GM->vertex[i]);
		for(j=0;j<GM->vertexnum;j++){
			if(GM->edgeweight[i][j]==maxvalue ){  //若权值为最大值
				printf("\tZ");                    //以Z表示无穷大
			}
			else{
				printf("\t%d",GM->edgeweight[i][j]);  //输出边的权值
			}
		}
		printf("\n");
	}
}

//开始遍历第n个节点
//将第n个节点标记为已访问
//输出第n个节点的值
//取出第n个节点的所有邻居节点
//对于每个未被访问的邻居节点m，执行以下步骤：
//递归调用深度优先遍历函数，以m为起点，继续遍历图
void deeptraone(Graphmatrix *GM, int n){     //从第n个结点开始，深度遍历图
	int i;
	GM->istrav[n]=1;         //标记该顶点已处理过
	printf("->%c",GM->vertex[n]);  //输出结点数据
	for(i=0;i<GM->vertexnum;i++){
		if(GM->edgeweight[n][i]!=maxvalue && !GM->istrav[n]){
			deeptraone(GM,i);    //递归进行遍历
		}
	}
}

void deeptraGraph(Graphmatrix *GM){   //深度优先遍历
	int i;
	for(i=0;i<GM->vertexnum;i++){    //清除各顶点遍历标志
		GM->istrav[i]=0;
	}
	for(i=0;i<GM->vertexnum;i++){
		if(!GM->istrav[i]){          //若该点未遍历
			deeptraone(GM,i);        //调用函数遍历
		}
	}
	printf("\n");
}

int main(){
	Graphmatrix GM;
	printf("input Graph type:");
	scanf("%d",&GM.Gtype);
	printf("input vertex num");
	scanf("%d",&GM.vertexnum);
	printf("input edge num:");
	scanf("%d",&GM.edgenum);
	clearGraph(&GM);
	createGraph(&GM);
	outgraph(&GM);
	deeptraGraph(&GM);
	return 0;
}

哒哒翔

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【图】图的相关基础知识

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。简言之，图是由节点以及它们之间的连线的集合，根据连线的不同又分为有向图和无向图。前面章节讲解中树结构的一个基本特点，是数据元素之间具有层次关系，每一层的元素可以和多个下层元素关联，但是只能和一个上层元素关联。如果把这个规则进一步扩展，也就是说，每个数据元素之间可以任意关联，这就构成了一个图结构。正是这种任意关联性，导致了图结构中数据关系的复杂性。
复制链接

扫一扫