线性规划之Google OR-Tools 简介与实战

最新推荐文章于 2024-04-26 15:56:55 发布

-派神-

最新推荐文章于 2024-04-26 15:56:55 发布

阅读量1.2w

点赞数 35

分类专栏：线性规划文章标签： OR-Tools 线性规划 google.AI 整数规划约束编程

本文链接：https://blog.csdn.net/weixin_42608414/article/details/109556196

版权

线性规划专栏收录该内容

6 篇文章 16 订阅

订阅专栏

最近我一直在从事线性规划方面的约束编程，主要使用的工具是google的or-tools,因此我在互联网上收集了一些有趣的优化问题的例子想给大家分享一下，这是or-tools的官网，里面有许许多多的例子，感兴趣的朋友可以自己去学习一下，我这里不再重复了。下面我先对or-tools的建模语言cp_model及其求解器CP-SAT Solver的使用技巧做一下简单介绍，随后对一些复杂的建模语法通过几个例子对大家详细讲解，以下素材均来自于互联网。

OR-Tools官网

https://github.com/google/or-tools/tree/master/examples

https://github.com/google/or-tools/tree/master/ortools/sat/samples

https://github.com/google/or-tools/tree/master/examples/contrib

基本语法

在or-tools中内置了一些第三方的开源求解器(SCIP, GLPK) 及商用求解器( Gurobi , CPLEX)，同时还有google自己的求解器Google's GLOP以及获得过多项金奖的CP-SAT。下面我们对CP-SAT的建模语法cp_model的使用技巧做一个总结，cp_model是一种很奇特的建模语法，它主要使用布尔型变量对优化问题进行建模，cp_model的基本使用方法请参照官网示例。

搜索所有最优解

如果你在求解一个优化问题的时候设置了一个目标如：model.Maximize或者model.Minimize，此时你将不能使用SearchForAllSolutions方法来搜索所有的解，为此我们可以使用以下两个步骤来搜索所有的解：

# Get the optimal objective value
model.Maximize(objective)
solver.Solve(model)

# Set the objective to a fixed value
# use round() instead of int()
model.Add(objective == round(solver.ObjectiveValue()))
model.Proto().ClearField('objective')

# Search for all solutions
solver.SearchForAllSolutions(model, cp_model.VarArraySolutionPrinter([x, y, z]))

非连续整形变量(Intvar)

我们可以使用以下非连续的变量作为整形变量 model.NewIntVar 的备选方法：

# List of values
model.NewIntVarFromDomain(
    cp_model.Domain.FromValues([1, 3, 4, 6]), 'x'
)

# List of intervals
model.NewIntVarFromDomain(
    cp_model.Domain.FromIntervals([[1, 2], [4, 6]]), 'x'
)

# Exclude [-1, 1]
model.NewIntVarFromDomain(
    cp_model.Domain.FromIntervals([[cp_model.INT_MIN, -2], [2, cp_model.INT_MAX]]), 'x'
)

# Constant
model.NewConstant(154)

Implications(单向约束/半约束)

Implications方法是一种单向的约束操作:a => b (a,b均为布尔型变量) ，a为True则b也为True,反之则不成立。

# a => b (both booleans)
model.AddImplication(a, b)

# a <=> b (better remove one of them)
model.Add(a == b)

# a or b or c => d
model.AddImplication(a, d)  # model.Add(d == 1).OnlyEnforceIf(a)
model.AddImplication(b, d)
model.AddImplication(c, d)

# a and b and c => d
model.Add(d == 1).OnlyEnforceIf([a, b, c])
or
model.AddBoolOr([a.Not(), b.Not(), c.Not(), d])

Iff, equivalence, boolean product

我们使用三个布尔变量来完成一个等价操作(双向约束)如：p <=> (x and y)

# (x and y) => p, rewrite as not(x and y) or p
model.AddBoolOr([x.Not(), y.Not(), p])

# p => (x and y)
model.AddImplication(p, x)
model.AddImplication(p, y)

上面我们使用了一句AddBoolOr和两句AddImplication实现了等价操作(双向约束)：p <=> (x and y)

If-Then-Else

我们需要引入一个中间变量来实现 if-else操作，假如我们要实现如下操作：

if x>=5 then:
y=10-x
else: y=0

如果我们要实现这样的if-else操作，我们需要引入一个bool中间变量：

b = model.NewBoolVar('b')

# Implement b == (x >= 5).
model.Add(x >= 5).OnlyEnforceIf(b)
model.Add(x < 5).OnlyEnforceIf(b.Not())

# First, b implies (y == 10 - x).
model.Add(y == 10 - x).OnlyEnforceIf(b)
# Second, not(b) implies y == 0.
model.Add(y == 0).OnlyEnforceIf(b.Not())

Solution hint / Warm start(解决方案提示/热启动)

如果我们在求解过程中加入一些变量的提示则可能加快求解速度。

num_vals = 3
x = model.NewIntVar(0, num_vals - 1, 'x')
y = model.NewIntVar(0, num_vals - 1, 'y')
z = model.NewIntVar(0, num_vals - 1, 'z')

model.Add(x != y)

model.Maximize(x + 2 * y + 3 * z)

# Solution hinting: x <- 1, y <- 2
model.AddHint(x, 1)
model.AddHint(y, 2)

Storing Multi-index variables（存储多索引变量）

推荐使用字段来存储多索引变量，这样便于理解。

employee_works_day = {
    (e, day): model.NewBoolVar(f"{e} works {day}")
    for e in employees
    for day in days
}

Linear Constraints（线性约束）

常用的线性约束有Add,AddLinearConstraint,AddLinearExpressionInDomain等几种:

#布尔数组work的和<=6
model.Add(sum(work[(i)] for i in range(10))<=6)

#布尔数组work的和>=2 and <=6
model.AddLinearConstraint(sum(work[(i)] for i in range(10)), 2, 6)

#布尔数组work的和 in [0,2,3,5] 
model.AddLinearExpressionInDomain(sum(work[(i)] for i in range(10)) ,[0,2,3,5])

Nonlinear Constraints（非线性约束）

常用的几种非线性约束如：绝对值约束、乘法约束、最大最小值约束

# Adds constraint: target == |var|
model.AddAbsEquality(target, var)

#Adds constraint: target == v1 * v2
model.AddMultiplicationEquality(target, [v1,v2])

#Adds constraint: target == Max(var_arr)
model.AddMaxEquality(target, var_arr)

#Adds constraint: target == Min(var_arr)
model.AddMinEquality(target, var_arr)

遗憾的是：没有一步到位的非线性表达式；必须建立复杂的使用中间变量逐段地生成数学表达式。

The AllDifferent Constraints（强制所有变量都不相同约束）

#Forces all vars in the array to take on different values
model.AddAddAllDifferent(var_arr)

protobuf

protobuf是google旗下的一款平台无关，语言无关，可扩展的序列化结构数据格式。所以很适合用做数据存储和作为不同应用，不同语言之间相互通信的数据交换格式，只要实现相同的协议格式即同一proto文件被编译成不同的语言版本，加入到各自的工程中去。这样不同语言就可以解析其他语言通过protobuf序列化的数据。

我们可以在or-tools中使用protobuf来序列化我们的模型

from google.protobuf import text_format
from ortools.sat.python import cp_model

model = cp_model.CpModel()
a = model.NewIntVar(0, 10, "a")
b = model.NewIntVar(0, 10, "b")
model.Maximize(a + b)

new_model = cp_model.CpModel()
text_format.Parse(str(model), new_model.Proto())

solver = cp_model.CpSolver()
status = solver.Solve(new_model)

print(solver.StatusName(status))
print(solver.ObjectiveValue())

The Element Constraint（元素约束）

# Adds constraint: target == var_arr[index]
# Useful because index can be a variable
# The var_arr can also contain constants!

model.AddElement(index, var_arr, target)

The Inverse Constraint（逆约束）

# The arrays should have the same size 𝑛 (can’t use dicts)
# The vars in both arrays can only take values from 0 to 𝑛 − 1
# Adds the following constraints:
# If var_arr[i] == j, then inv_arr[j] == i
# If inv_arr[j] == i, then var_arr[i] == j
# Intuition: sets up a “perfect matching” between the two sets of variables

model.AddInverse(var_arr, inv_arr)

Interval Variables (区间变量)

CP-SAT有一种特殊的区间变量，它可以用来表示时间间隔。

# Represents an interval, enforcing start - end == duration
# start, end, duration can be constants or variables!
# Note: there is no way to access start, end, duration of an interval by default
# Recommended: directly add them as fields of the interval object

model.NewIntervalVar(start, duration, end, name)

NoOverlap Constraint (不重叠约束)

当我们创建了一组区间变量以后，有时候我们希望区间变量之间的时间间隔不能发生重叠，这时我们可以使用AddNoOverlap约束。AddNoOverlap会强制所有的时间间隔变量不发生重叠,不过它们可以使用相同的开始/结束的时间点。

# Note: there is no way to access start, end, duration of an interval by default
# Recommended: directly add them as fields of the interval, e.g.
#  interval.start = start

model.AddNoOverlap(interval_arr)

# Powerful constraint: enforces that all intervals in the array do not overlap with each other!
# It’s OK to have shared start/endpoints

Parallelization（并行化）

我们可以使用多个线程并行运行求解器求解

solver = cp_model.CpSolver()
solver.parameters.num_search_workers = 8 #CPU内核数

Optimization with CP-SAT (CP-SAT的优化目标)

我们可以使用最大化/最小化一个表达式来实现优化的目标，例如：

model.Minimize(5*a+2*b-c)
# or
model.Maximize(sum(x[i] for i in range(10))

这里需要指出的是当我们使用带权重的优化目标组合时如上面的5*a+2*b-c，权重代表了优化目标的优先级顺序,权重越大则优先级越高，但给权重赋值时需要考虑如下因素：

假如我们要优化a,b两个目标(目标最小化)，我们希望优先优化a，然后是b，那么我们要给a赋一个较大的权重,如5，而给b赋一个较小的权重如 2, 但是如果此时5*a的值小于2*b的值，那么Minimize的时候仍然会优先优化b而不是a ,这是因为当b减少的时候目标的下降速率要高于a减小时的下降速率,因此结果会优先优化b。为了解决优先优化a的目标，我们应该进一步提高a的权重，只有当N*a>2*b, 才会优先优化a。另外在使用Minimize(Maximize)优化时，我们希望其中的一个目标最大化(最小化),那么我们可以给该目标赋一个带负值的权重，比如上面的c.

上面我们对CP-SAT的建模语法做了一个简单的介绍，下面我们来举一些即简单又复杂的有趣例子：

OR-Tools实战

破译密码

有下面一个加密的加法算式,其中每个字母代表一个数字，不同的字母代表不同的数字,希望你能破解这些字母所代表的数字:

下面我们就让or-tools怎么破解这些字母：

首先初始化模型并创建变量,每个字母创建一个整形变量:

from ortools.sat.python import cp_model

#初始化模型,并创建变量
model = cp_model.CpModel()
S = model.NewIntVar(1,9, 'S')
E = model.NewIntVar(0,9, 'E')
N = model.NewIntVar(0,9, 'N')
D = model.NewIntVar(0,9, 'D')
M = model.NewIntVar(1,9, 'M')
O = model.NewIntVar(0,9, 'O')
R = model.NewIntVar(0,9, 'R')
Y = model.NewIntVar(0,9, 'Y')

然后我们添加加法算式和约束，这里我们用到了AddAddAllDifferent约束，因为我们要让每一个字母都代表不同的数字。

#添加约束
model.Add(   1000*S + 100*E + 10*N + D
           + 1000*M + 100*O + 10*R + E
== 10000*M + 1000*O + 100*N + 10*E + Y)

model.AddAllDifferent([S,E,N,D,M,O,R,Y])

最后我们求解，并打印结果：

#求解并打印结果
solver = cp_model.CpSolver()
if solver.Solve(model) == cp_model.OPTIMAL:
    print([f'{v}={solver.Value(v)}' for v in [S,E,N,D,M,O,R,Y]])

结果为：

Magic Sequence（魔术序列）

魔术序列指的是这样一组数字序列：s1,s2......sn. 其中 s(i)的值表示下标 i 在序列中出现的次数。如n=4的魔术序列为：

我们看到s0的值等于2 表示下标0在序列中出现了2次，s1的值等于1表示下标1在序列中出现了1次。s3的值等于0表示下标3在序列中出现了0次。如何找出给定序列长度n的魔术序列呢？下面我们让or-tools来完成这个工作：

首先我们必须要创建一个整形数组用来存放该魔术序列的值，为了对该魔术序列的值进行约束，我们还必须引入一个二维的布尔型矩阵eq，它的作用是对魔术序列的值进行约束，这里我们会使用OnlyEnforceIf约束，这是一个非常常用的单向约束（𝑏 ⇒ 𝑐），同时可以很方便的组合两个OnlyEnforceIf约束，让它变成一个双向约束(𝑏 ⇔ 𝑐)。

from ortools.sat.python import cp_model
model = cp_model.CpModel()

S={}
n=4
for i in range(n+1):
    S[i] = model.NewIntVar(0,n+1,f's_{i}')  # 创建初始化魔术序列s
    

eq={}
for i in range(n+1):
    for j in range(n+1):
        eq[i,j] = model.NewBoolVar(f's_{i}=={j}') # 创建布尔型二位矩阵
        model.Add(S[i] == j).OnlyEnforceIf(eq[i,j]) # 只要eq[i,j]等于1,则 S[i] == j
        model.Add(S[i]!=j).OnlyEnforceIf(eq[i,j].Not()) # 只要eq[i,j]等于0,则 S[i] != j

上面我们初始化了模型，并创建初始化魔术序列s,和布尔型约束矩阵eq, 同时我们将eq和S进行了绑定, 我们用eq来约束S,他们之间是一个双向约束(用两个单向约束来实现双向约束)，即用eq的每一行来约束对应的s(i),只要该行的eq[i,j]=1, 就将 j 赋值给对应的s(i),如果eq[i,j]=0,则对应的s[i]不能等于 j :

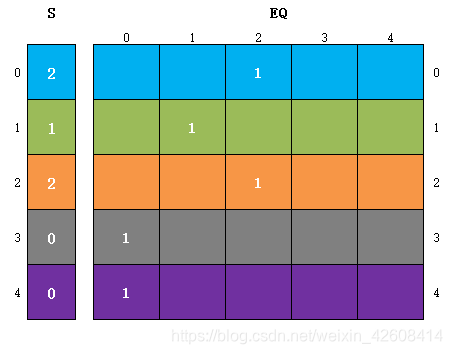
上面我们是从EQ的行的方向来对S(i)进行约束，下面我们要从EQ列的方向对S(i)进行约束，我们要对EQ每一列的求和，并让这个和等于对应的S(i):

for i in range(n+1):
    model.Add(S[i]==sum(eq[j,i] for j in range(n+1)))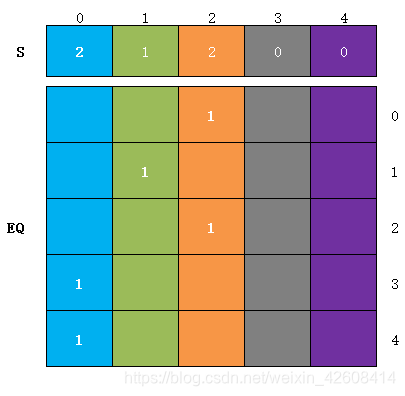

下面我们求解该模型并打印结果：

solver = cp_model.CpSolver()
status = solver.Solve(model)
print("n :",n)
print([f's_{i}={solver.Value(S[i])}' for i in range(n+1)])

当我们将n设置为5时，魔术序列无解,即不存在n=5的魔术序列，当n=6至10的魔术序列为：

AddBoolOr 约束的研究

or-tools的逻辑关系约束中有一个AddBoolOr() 约束，该约束会让初学者搞不懂它的使用方法而感到困惑，而AddBoolOr()又很常用，它经常和AddImplication()搭配使用来完成一个双向约束, 当然也可以使用OnlyEnforceIf()约束来替代AddBoolOr和AddImplication组合。从官方文档的说明中可知AddBoolOr 接受一个布尔数组作为参数, 而AddBoolOr 结果必须为True，也就是说这个布尔数组的每个元素经过 or 运算以后结果必须为True。因此AddBoolOr的功能就是要让它的参数(布尔数组)经过 or 运算后结果为True. 下面我们来看一个例子：

球队比赛安排计划，要求是这样的：任意一个球队在完成连续两个主场的比赛后，下一场必须去客场，同理任意一个球队在完成连续两个客场的比赛后，下一场必须去主场。也就是说每个球队主客场连续比赛的次数不能超过2次。下面我们来看一个代码片段：

a = model.NewBoolVar('home day1')
b = model.NewBoolVar('home day2')
c = model.NewBoolVar('break')

model.AddBoolOr([a.Not(), b.Not(), c])
model.AddBoolOr([a, b, c])
model.AddBoolOr([a.Not(), b, c.Not()])
model.AddBoolOr([a, b.Not(), c.Not()])

运行这段代码后会得到如下的真值表：

这里 a = 1 表示第一天在主场比赛，a = 0 表示第一天在客场比赛。
这里 b = 1 表示第二天在主场比赛，b = 0 表示第二天在客场比赛。
这里 c= 0 表示下一场不需要交换场地，而 c= 1 表示下一场需要交换场地。

这里的真值表满足了我们的要求即：每个球队主客场连续比赛的次数不能超过2次。那上述代码中的4句AddBoolOr()约束是如何实现这样的真值表呢？下面我们来分析每一句AddBoolOr的内在逻辑，首先我们看第一句，我们单独执行这句：

model.AddBoolOr([a.Not(), b.Not(), c])

因为AddBoolOr的结果必须为True的，因此当 c = 1 时，a.Not()与b.Not() 可以为任意值, 而当 c = 0 时, a.Not()与b.Not()之中至少要有一个为 1。因此这句代码会产生下面的真值表：

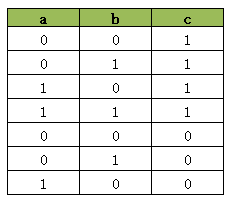
这里我们发现为了要让 AddBoolOr([a.Not(), b.Not(), c]) 的结果为True, 真值表中必须排除[1, 1, 0] 这个组合。因为[1, 1, 0] 会时AddBoolOr([a.Not(), b.Not(), c]) 的结果为False,这是不允许的。

接下来，我们单独执行第二句 AddBoolOr代码：

model.AddBoolOr([a, b, c])

同样因为AddBoolOr的结果必须为True的，因此当 c = 1 时，a与b 可以为任意值, 而当 c = 0 时, a与b之中至少要有一个为 1。因此这句代码会产生下面的真值表：

这里我们发现为了要让 AddBoolOr([a, b, c]) 的结果为True, 真值表中必须排除[0, 0, 0] 这个组合。因为[0, 0, 0] 会时AddBoolOr([a, b, c]) 的结果为False,这是不允许的。

接下来我们同时执行上述两句AddBoolOr约束看看结果会怎样：

model.AddBoolOr([a.Not(), b.Not(), c])
model.AddBoolOr([a, b, c])
# model.AddBoolOr([a.Not(), b, c.Not()])
# model.AddBoolOr([a, b.Not(), c.Not()])

同时执行上述两句AddBoolOr约束会产生如下真值表：

仔细观察这个真值表，它正是单独执行上述两个AddBoolOr约束所产生的两个真值表的交集，它从AddBoolOr([a.Not(), b.Not(), c])的真值表中排除了[0, 0, 0], 从AddBoolOr([a, b, c])的真值表中排除了[1, 1, 0], 因此我们可以推断同时执行两句AddBoolOr，所产生的真值表是单独执行AddBoolOr产生的真值表的交集。

下面我们单独执行第三句model.AddBoolOr([a.Not(), b, c.Not()]) ：

model.AddBoolOr([a.Not(), b, c.Not()])

因为AddBoolOr的结果必须为True的，因此当 c = 1 时c.Not()=0，因此a.Not()与b 之中至少要有一个为 1，而当 c = 0 时c.Not()=1, 因此a.Not()与b可以为任意值,。因此这句代码会产生下面的真值表：

这里我们发现为了要让 AddBoolOr([a.Not(), b, c.Not()]) 的结果为True, 真值表中必须排除[1, 0, 1] 这个组合。因为[1, 0, 1] 会使AddBoolOr([a.Not(), b, c.Not()]) 的结果为False,这是不允许的。

下面我们单独执行第四句model.AddBoolOr([a, b.Not(), c.Not()])：

model.AddBoolOr([a, b.Not(), c.Not()])

因为AddBoolOr的结果必须为True的，因此当 c = 1 时c.Not()=0，此时a与b.Not() 之中至少要有一个为 1，而当 c = 0 时c.Not()=1, 此时a与b.Not()可以为任意值,。因此这句代码会产生下面的真值表：

这里我们发现为了要让 AddBoolOr([a, b.Not(), c.Not()]) 的结果为True, 真值表中必须排除[0, 1, 1] 这个组合。因为[0, 1, 1] 会使AddBoolOr([a, b.Not(), c.Not()]) 的结果为False,这是不允许的。

下面我们同时执行第三句和第四句AddBoolOr约束看看会得到什么样的结果:

# model.AddBoolOr([a.Not(), b.Not(), c])
# model.AddBoolOr([a, b, c])
model.AddBoolOr([a.Not(), b, c.Not()])
model.AddBoolOr([a, b.Not(), c.Not()])

与同时执行第一句和第二句AddBoolOr的结果类似，同时执行第三句和第四句AddBoolOr约束我们会得到单独执行第三句和第四句所产生的两个真值表的交集：

仔细观察这个真值表，它正是单独执行第三和第四个AddBoolOr约束所产生的真值表的交集，它从AddBoolOr([a.Not(), b, c.Not()])的真值表中排除了[0, 1, 1], 从AddBoolOr([a, b.Not(), c.Not()])的真值表中排除了[1, 0, 1]。

最后我们同时执行四句AddBoolOr，我们会得到上述两个两两同时执行的AddBoolOr约束的真值表的交集。

model.AddBoolOr([a.Not(), b.Not(), c])
model.AddBoolOr([a, b, c])
model.AddBoolOr([a.Not(), b, c.Not()])
model.AddBoolOr([a, b.Not(), c.Not()])

使用`OnlyEnforceIf来代替`AddBoolOr

由于对AddBoolOr结果的理解需要借助于真值表，因此给我们在使用AddBoolOr约束的时候增加了难度，有没有一种更容易理解的表达式来它可以实现AddBoolOr的功能呢？那应该就是非OnlyEnforceIf莫属了，下面我们来看一下如果使用OnlyEnforceIf来代替之前的四句AddBoolOr来实现球队比赛安排计划：

model.Add(a == b).OnlyEnforceIf(c)
model.Add(a != b).OnlyEnforceIf(c.Not())

OnlyEnforceIf可以表示为：当且仅当，上述两句OnlyEnforceIf表达的含义是: 当且仅当c = True时，则a和b值必须相同，同时当且仅当c = False时，则a和b值必须不相同。执行上述两句代码后所产生的真值表为：

这个真值表与我们用四句AddBoolOr所生成的真值表示一样的。并且OnlyEnforceIf 的逻辑更容易理解。下面我们看看只执行一句OnlyEnforceIf会产生什么样的结果：

model.Add(a == b).OnlyEnforceIf(c)
# model.Add(a != b).OnlyEnforceIf(c.Not())

当我们只执行第一句 Add(a == b).OnlyEnforceIf(c) 时得到下面的结果：

这个结果与两个AddBoolOr([...，c.Not() ]约束组合的效果相同。同样仅执行 Add(a != b).OnlyEnforceIf(c.Not()) 其结果与两个AddBoolOr([...，c]约束的组合效果相同。那既然OnlyEnforceIf那么容易理解，使用那么方便，那为什么还要使用AddBoolOr这种难以理解的语法呢？

其实通过对AddBoolOr和OnlyEnforceIf输出日志的研究，我们发现OnlyEnforceIf 只不过是一个绣花枕头而已,其内部的实现仍然由AddBoolOr来完成，他们就好比是Keras 和 Tensorflow之间的关系。OnlyEnforceIf 在真正执行的时候，其内部仍然会被替换成AddBoolOr。也就是说上述两句OnlyEnforceIf在执行的时候会被四句AddBoolOr替代，只是我们看不见而已。

火车路线分配问题

有若干辆火车组成的车队，每天需要给每辆火车分配运输路线，运输路线分配的约束条件是：

1.每列火车每天必须至少被分配一条路线（不得出现火车闲置的情况）。

2.必须将每列火车分配到至少一条路线（最多两条路线），并且必须覆盖所有路线。

3.分配给路线的火车最终里程不得超过24800（即前一天的累积里程+分配的路线里程<= 24800）。

4.如果一天中将火车分配了两条路线，则这两条路线的运行时间不得重叠。

5.前一天行驶里程高的火车应该分配到短途，前一天行驶里程低的火车应该分配到长途(这是一个软约束，应尽量满足)。

下面是数据的格式：

我有一个存储火车数据的dataframe。可以随机选择一个日期，并查看所有火车中每列火车直到前一天结束时的累积里程：

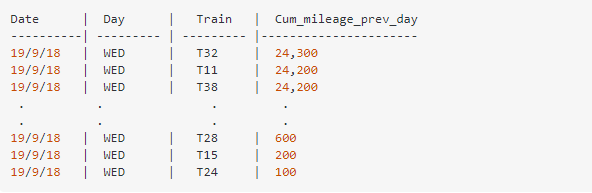
运输路线的dataframe如下图所示。请注意，高于100公里的路线被定义为长路线，低于100公里路线则为短路线。

我想要的最终结果是这样的：每列火车已分配了1条或2条路线，并且显示了当天结束时的总里程：

初始化数据

以上是火车运输路线的业务需求，下面我们使用OR-Tools的CP-SAT模型来求解该问题，首先我们创建初始化数据：

import datetime
from itertools import combinations
from datetimerange import DateTimeRange
from ortools.sat.python import cp_model

# 路线里程
route_km = {
    'R11': 700,
    'R32': 600,
    'R16': 600,
    'R41': 10,
    'R42': 10,
    'R43': 10,
    'R44': 10,
    'R45': 10}

#火车累积行驶里程
train_cum_km = {
    'T32': 24_300,
    'T11': 24_200,
    'T38': 24_200,
    'T28': 600,
    'T15': 200,
    'T24': 100}

#路线时刻表
route_times = {
    'R11': ('05:00', '00:00'),
    'R32': ('06:00', '00:50'),
    'R16': ('05:20', '23:40'),
    'R41': ('11:15', '12:30'),
    'R42': ('11:45', '13:00'),
    'R43': ('12:15', '13:30'),
    'R44': ('12:45', '14:00'),
    'R45': ('13:20', '14:35')}

trains = list(train_cum_km.keys())
routes = list(route_km.keys())
num_trains = len(trains)
num_routes = len(routes)

定义函数

接下来我们要定义一个判断两个时间段是否重叠的函数，因为判断两个时间段是否重叠的逻辑比较复杂，所以我们决定使用一个python的datetimerange包，datetimerange包内置了判断两个时间段是否重叠的方法，使用起来非常方便：

from datetimerange import DateTimeRange

#检查时间范围是否重叠
def check_overlap(t1_st, t1_ed, t2_st, t2_ed):
    t1_st_dt=datetime.datetime.strptime(t1_st, '%H:%M')
    t1_ed_dt=datetime.datetime.strptime(t1_ed, '%H:%M')

    t2_st_dt=datetime.datetime.strptime(t2_st, '%H:%M')
    t2_ed_dt=datetime.datetime.strptime(t2_ed, '%H:%M')

    if t1_ed_dt <= t1_st_dt: # 跨天则修改t1_ed_dt的日期
        t1_ed_dt += datetime.timedelta(days = 1)

    if t2_ed_dt <= t2_st_dt: # 跨天则修改t2_ed_dt的日期
        t2_ed_dt += datetime.timedelta(days = 1)
        
    t1_range = DateTimeRange(t1_st_dt.strftime('%Y-%m-%d %H:%M:%S'), 
                             t1_ed_dt.strftime('%Y-%m-%d %H:%M:%S'))
    t2_range = DateTimeRange(t2_st_dt.strftime('%Y-%m-%d %H:%M:%S'), 
                             t2_ed_dt.strftime('%Y-%m-%d %H:%M:%S'))
    
    return t1_range.is_intersection(t2_range)

创建约束变量

接下来我们定义一个约束变量assignments，它是一个二维的布尔数组,用来存放火车和路线的分配结果：

model = cp_model.CpModel()
solver = cp_model.CpSolver()

#创建约束变量
assignments = {(t, r): model.NewBoolVar('assignment_%s%s' % (t, r)) for t in trains for r in routes}

约束1: 每条路线只能分配给1列火车

for r in routes:
    model.Add(sum(assignments[(t, r)] for t in trains) == 1)

约束2: 必须将每列火车分配到至少一条路线（最多两条路线）

这里我们可以使用两条model.Add()语句来实现一个区间约束，不过也可以使用一条AddLinearConstraint()来实现同样的功能。

for t in trains:
    #model.Add(sum(assignments[(t, r)] for r in routes) >= 1)
    #model.Add(sum(assignments[(t, r)] for r in routes) <= 2)
    model.AddLinearConstraint(sum(assignments[(t, r)] for r in routes),1,2)

约束3:

分配给路线的火车最终里程不得超过24800（即前一天的累积里程+分配的路线里程<= 24800）

这里我们没有使用<=这样的判断，而是定义了一个整形数组，它的元素取值范围是在0至24800之间，然后用"=="来取代"<= "。这是CP_SAT推荐使用的一种方法。

day_end_km = { t: model.NewIntVar(0, 24_800, 'train_%s_day_end_km' % t) for t in trains }
for t in trains: 
    model.Add(sum(assignments[t, r]*route_km[r] for r in routes) + train_cum_km[t] == day_end_km[t])

约束4：分配给火车的任意两条路线时间上不能重叠

for (r1, r2) in combinations(routes, 2):
    if check_overlap(route_times[r1][0], route_times[r1][1], route_times[r2][0], route_times[r2][1]):
         for train in trains:
            model.AddBoolOr([assignments[train, r1].Not(), assignments[train, r2].Not()])

这里我们使用了AddBoolOr(Not(), Not())方法，需要搞明白的是该方法排除了[1, 1]这种情况的出现，因为[1, 1] 会使AddBoolOr(Not(), Not())的结果为False，这是不允许的, 这里[1, 1]代表了两个时间段重叠的情况。

约束5: 软约束

前一天行驶里程高的火车应该分配给短途路线，前一天行驶里程低的火车应该分配给长途路线

score = {(t,r): route_km[r] + train_cum_km[t] for t in trains for r in routes }
model.Minimize(sum(assignments[t,r]*score[t,r] for t in trains for r in routes))

求解

status = solver.Solve(model)
assert status in [cp_model.FEASIBLE, cp_model.OPTIMAL]

for t in trains:
    t_routes = [r for r in routes if solver.Value(assignments[t, r])]
    print(f'Train {t} 分配路线: {t_routes}',','
          f'总累积行驶里程: '
          f'{solver.Value(day_end_km[t])}')

问题小结

不知道读者有没有发现，我们这里设置的优化目标是否有问题？，它是否满足了约束5的要求? 如果不能满足约束5的要求那应该如何来修改我们的优化目标？约束5的要求是：前一天行驶里程高的火车应该分配给短途路线，前一天行驶里程低的火车应该分配给长途路线。我想这个问题留给读者来思考吧！

参考文档

以上素材均来自互联网，本文作者对原始素材进行了修改、完善和补充，有不足之处请读者们指出。以下是几个案例的出处：

https://stackoverflow.com/questions/57062032/google-or-tools-train-scheduling-problem

https://activimetrics.com/blog/ortools/cp_sat/addboolor/

https://www.xiang.dev/cp-sat/#

-派神-

关注

35
点赞
踩
62

收藏

觉得还不错? 一键收藏
打赏
24
评论
线性规划之Google OR-Tools 简介与实战

最近我一直在从事线性规划方面的约束编程，主要使用的工具是google的or-tools,因此我在互联网上收集了一些有趣的优化问题的例子想给大家分享一下，这是or-tools的官网，里面有许许多多的例子，感兴趣的朋友可以自己去学习一下，我这里不再重复了。下面我先对or-tools的建模语言cp_model及其求解器CP-SAT Solver的使用技巧做一下简单介绍，随后对一些复杂的建模语法通过几个例子对大家详细讲解，以下素材均来自于互联网。OR-Tools官网https://github...
复制链接

扫一扫