＜医学断层图像三维重建面绘制算法的研究＞——第一遍阅读

医学断层图像三维重建面绘制算法的研究

参考文献：段正华. 医学断层图像三维重建面绘制算法的研究[D].哈尔滨理工大学,2020.

基于边增长的三维重建面绘制算法。在整个算法三维重建的插值上，提出了一种三段插值法，该方法具有较好的插值效率和重建精度。同时，整个算法拥有一个队列用于存储增长边信息，两个数组记录各个立方体体素的处理信息和增长信息。

医学断层图像三维重建算法主要分为面绘制(Surface Rendering)算法和体绘制(Volume Rendering)算法[23]。面绘制算法，它先通过二维的断层图像进行特征的提取，然后用中间几何图片(主要有四边形、三角形、六面体、锥体和四面体等)去拟合原有物体的三维曲面轮廓[24]，最后利用计算机图形学对所重建的几何图元进行显示。

1.2.2 医学断层图像三维重建面绘制算法的研究现状

医学断层图像三维重建面绘制算法在算法上细分，又分为切片级算法和体素级算法[23,26]。

第2章 医学断层图像三维重建的基本流程

从医学断层图像三维重建的输入和输出来看，它是一个从二维断层图像到三维模型可视化过程。在实际应用中，对图像的三维重建主要分为两种：一种直接将输入的数据通过三维重建算法生成三维模型；另一种方式为了得到质量较好的三维模型，它需要先对输入的二维断层图像进行预处理，然后再使用三维重建算法生成三维模型。在第二种重建方式中，对于面绘制算法，有时在重建之前还需要对图像进行分割；在三维模型生成之后有时也还需要对三维网格模型进行一定的后续操作处理，使最后的网格模型更利于储存和渲染等。

2.1 医学断层图像的预处理

在对医学断层图像进行三维重建之前，对于那些噪声较多或者特征不明显的图像，通常需要对其进行滤波或增强处理[41]。

2.2 医学断层图像的分割

医学图像分割的目的是把需要的目标组织所对应的图像区域从整个图像中抽取出来。图像分割的质量直接关系着后续面绘制算法的重建结果，分割有时也被作为一种加速面绘制算法重建的技术手段[32]。图像分割的主要依据是各个组织在图像灰度值上表现出来的差异性。

2.3 医学断层图像的三维重建算法

在应用时，面绘制算法主要用来重建组织的外部轮廓，体绘制主要观察各个组织之间的相互关系和组织模型大小。融合绘制方法是一种结合了面绘制和体绘制的重建算法，一般利用在细节方面表现优秀的面绘制重建物体的外部轮廓，用体绘制重建物体的内部组织，然后将两者重建的结果进行叠加渲染。

面绘制算法主要有轮廓连接法、立方体算法(Cuberille)、分解立方体算法(DC)、移动立方体算法(MC)、移动四面体算法(MT)等。在实际应用中，面绘制算法使用最多的是 MC 算法或者是 MC 算法的改进版本。

体绘制算法主要分为两类[55-57]：一类是从屏幕显示结果的二维图像出发进行处理的以图像空间为序的体绘制算法；另一类是从输入的三维数据场出发进行处理的以物体空间为序的体绘制算法。以图像空间为序的体绘制典型算法是光线投影算法；常用的以物体空间为序的算法有：抛雪球法、纹理映射法、错切变形法等。现如今随着硬件技术的快速发展，越来越多研究者以 GPU 来改进体绘制算法的三维重建[58-61]。

体绘制的核心思想就是模拟光线在三维体数据中传播的过程，将最后的光线强度显示在屏幕上。它假定连续的三维体数据是一些小粒子，这些具有一定的光学效应，基于这种假定和光线的光学效应总结成了如下几种光学模型：光线吸收模型、光线发射模型、光线吸收和发射模型[62]，图 2-4 为体绘制重建人体胸部的效果。

第3章 基于边增长的三维重建面绘制算法

3.1 MC算法的概述

等值面可以理解为具有相同灰度值像素点的组合，用数学公式表示为：
$$(x,y,z)|f(x,y,z)=c$$
其中，x、y 和 z 代表数据在三维空间中采样数据点对应的坐标；$f(x,y,z)$表示三维数据场中坐标为$f(x,y,z)$点对应的灰度值；c 为重建时一个常数，称为阈值，即等值面所对应的像素灰度值。在应用中，很少有像素灰度值直接等于阈值的，所以通常采用插值的方式求解灰度值与阈值相等的等值点。

MC 算法将立方体 8 个顶点的灰度值和等值面的阈值进行比较，根据各个顶点灰度值与阈值的大小将立方体分为 2⁸=256种，通过反对称性和旋转对称性，最后将这 256 种归纳为了 15 种基本拓扑构型，如图 3-2 所示。

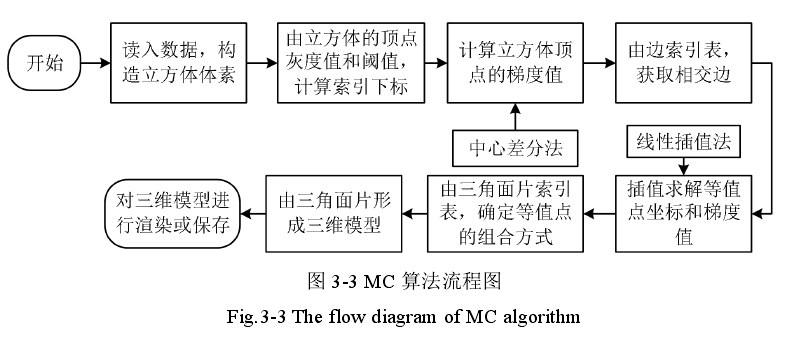
在 MC 算法的三维重建过程中，它通过遍历的方式，根据各个立方体体素对应的拓扑构型，依次提取各个立方体体内的等值面。为了能够快速的进行断层图像的三维重建，MC 算法对 256 种立方体设定了对应的边索引表和三角面片索引表。其中边索引表共有 256 组，每一组由 12 位的二进制数值表示，它展示了立方体 12 条边与等值面的相交情况，根据该表利用线性插值的方法求出边与等值面的交点。三角面片索引表也有 256 组，每一组给出了对应立方体中的三角面片是由那些边上交点组合而成的，同时还给了立方体内三角面片的个数，一个立方体中最多可能有5个三角形，每个三角形有三条边上的交点构成，一般每一组用16个数来表示三角形顶点所在边的情况，多出来的一个数用来做哨兵结点。综上所诉，MC 算法主要用边索引表来插值求出边上交点的空间坐标和梯度值，用三角索引表将各个边上交点组合成三角面片网格。当 MC 算法提取完所有立方体体内的等值面网格后，就可以对生成的三维模型进行保存或者渲染了。图 3-3 为 MC 算法重建的整个流程。

3.2 基于边增长的三维重建面绘制算法

本文提出了一种基于边增长的三维重建面绘制算法，算法的核心就是利用已存在的等值面去生成相邻立方体内的等值面。

基于边增长的三维重建面绘制算法拥有一个增长队列和两个标记数组，队列中存储着增长边信息，标记数组记录着各个立方体的处理情况与立方体的增长信息放入了增长队列里面的情况。其中，增长边信息具体包括边上两个端点的三维空间坐标、两个端点的梯度值以及增长边要增长到的立方体坐标。

基于边增长的三维重建面绘制算法的步骤主要如下：
步骤一：选取种子三角形，并把种子三角形形成的增长边放入增长队列中。
步骤二：从增长队列中取出增长边信息，并构造出要增长到的立方体信息(通过增长边将要被处理的立方体信息)。
步骤三：根据拓扑构型插值求解出等值面与立方体边的交点，并把交点进行连接组合成三角形网格。
步骤四：判断步骤三中等值面与立方体表面相交生成的新边是否作为增长边，把可以作为增长边的新边放入增长队列里面。
步骤五：重复步骤二三四，直到队列为空。

3.3 种子三角形的选取

本文按照图 3-2 中给出的 MC 算法 15 种基本拓扑构型的顺序，对应图 3-6 的四组实验，统计了四组实验中有等值面 14 种拓扑构型的数量，然后根据各个拓扑构型的数量换算成了它们各自所占的比例。得到了如下的数据：

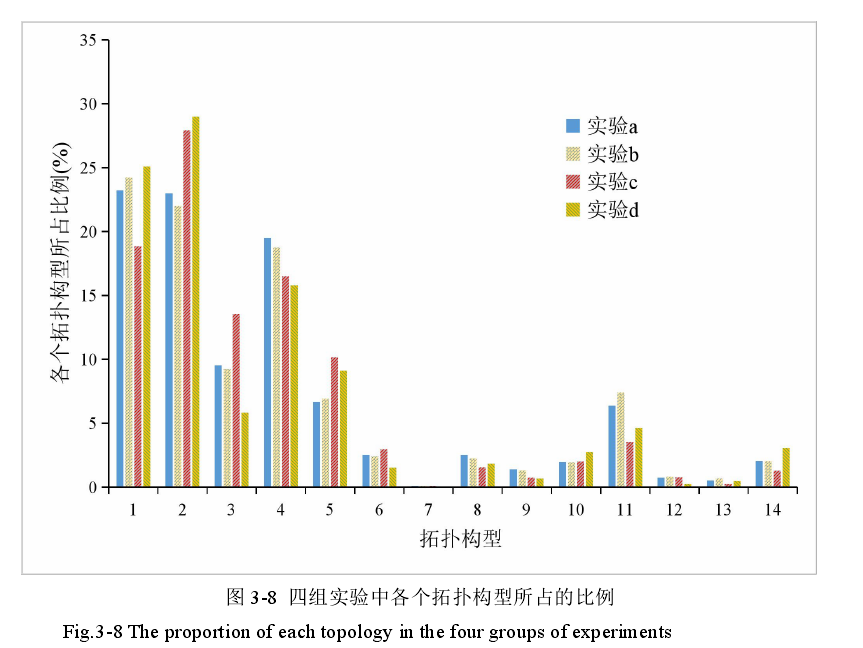
可以看出，拓扑构型 1、2 和 4 占据了绝大部分比重。

基于拓扑构型 1 的简单性和占比高的原因，对图 3-6 的图像再次进行了重建，采用图3-6相同的输入数据和重建阈值，但只对含有拓扑构型 1 的立方体进行重建，重建效果如图 3-10 所示。

可以看到，图3-10基本上也能够反映物体的大致轮廓，且各个独立的三角面片均匀的分布在了各个横截面上。所以采用拓扑构型1的三角形作为种子三角形，然后以种子三角形的边作为增长边进行增长重建。

3.4 立方体信息的构造

在对立方体体素进行处理之前需要构造立方体的相关信息，需要构造的立方体信息有：==立方体的各个顶点的灰度值、空间三维坐标值和梯度值。==其中灰度值和三维坐标主要用来计算立方体体内等值面的空间三维信息；梯度值用来计算三角形的法向量，以便利用计算机图形学渲染最后生成的三维模型。

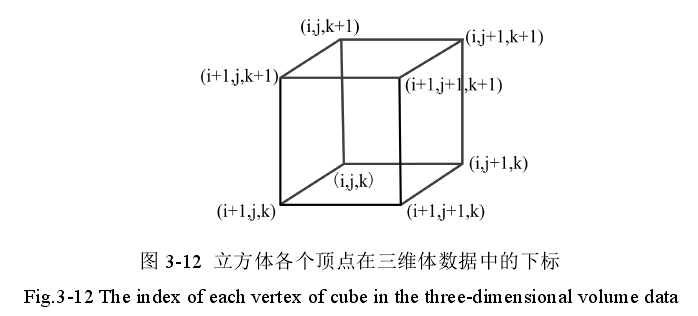
假设输入三维数据的大小为 $X\times Y\times Z$ ，立方体在三个方向的边长分别为a、b和c 。对于下标为$($