图的基本概念和Dijkstra算法

最近看离散数学图的部分根据自己的理解，整理了一下笔记

图的基本概念

这里所说的图是一种抽象的数学概念，并不是图片图像什么的，类似质点的概念，只不过可以用图行化表示出来。比如有四个城市{A，B，C，D}，我们想要描述他们之间的公路连通关系，我们画四个点，称为顶点（图中的顶点数>0），表示这四个城市

Fig1

这也算一个图了，但是顶点之间没有关系，这个关系称为边，这样的图被称为零图，对于没有边的任何一个顶点都是孤立顶点，上面就有A，B，C，D四个孤立顶点。

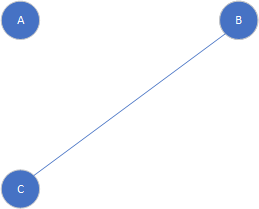
然后在相互之间连线表示互相连通，有以下的图，其中(A，B)互相连通，(A,D)不连通，其他同理

Fig2

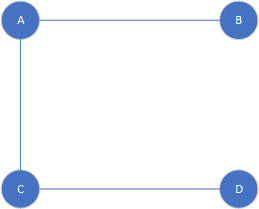
上面说的是简单图，简单图指的是没有环和平行边的图，如果有平行边（即两个顶点之间有多条边，则他们是平行的），则这个图是多重图

Fig3

如果有环会出现以下情况（即一个顶点到自身有一条边，这条边就是环），下面的顶点B就有一个环，但这个属于多重图和简单图

FIg4

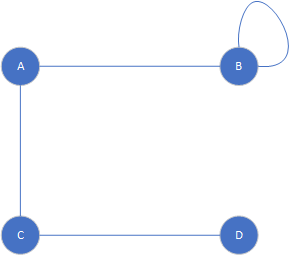
实际研究学习的时候，还接触到HyperGraph，读者可以自行到维基了解。

图的同构

由于图是一种抽象关系的描述工具，实际上，我们如果把简单图中的A，B，C，D，换成E，F，G，H（如下图所示），他们表示的图也是相同的

Fig5

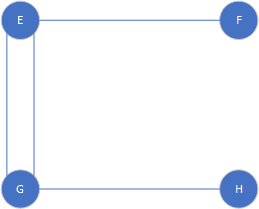
而在实际作图的过程中，每个城市可能会根据数量关系（之后介绍，即关于集合的部分）有不同的方式去画同一幅图，我们并不关心怎么画这图，而关注的是他们之间的关系，这样的图也是相同的。我们称这样两个相同的图是同构的。如下图所示，

Fig6

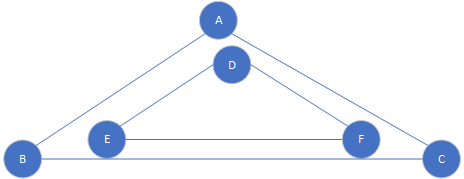
Fig7

子图

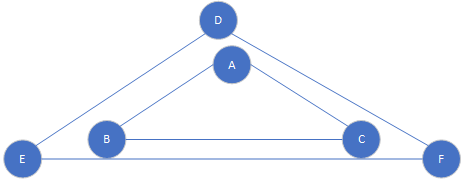
如果我们在某些场景下只需要表示，一个图部分顶点和部分边，就产生了子图的概念，最开始的图称为母图（也有称为始图的），而子图是保留母图中的部分顶点和部分边的结果（不能产生新的边），即顶点集合是母图的非空子集，边集合也是母图的子集。依旧拿上面的简单图A，B，C，D来说，以下都是它的子图，（当然还有很多）

去掉顶点的子图（顺带去掉了相应边）

Fig8

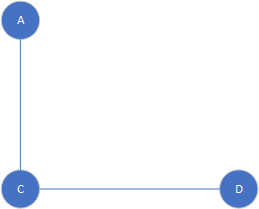
只去掉边的子图

Fig9

说到子图，不得不说一下子图相关概念，其中就有支撑子图，支撑子图指的是母图中所有的顶点都在子图中，但是母图中边可以不用都在子图里面，毕竟还是子集嘛，比如只去掉边的子图Fig9也是支撑子图，显然下面的图也是，（当然还是不止这些）

Fig10

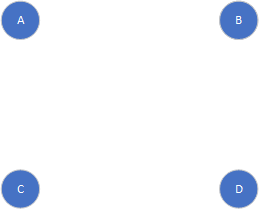
其次还要说一下，诱导子图，诱导子图其实还是比较简单的，就是有一个子图，如果它包含了母图中的某些点，那么它必须包含这些点在母图中对应的边（如果之前顶点之间没有边就不管），所以上面只去掉边的子图Fig9的例子就不是诱导子图了，去掉顶点的子图Fig8的例子恰好是一个诱导子图，下面再举一个例子，没有顶点C的诱导子图
Fig11

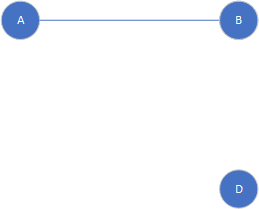
补图

如果母图去掉子图包含所有的边剩下的图（节点数与母图相同），称为相对补图

子图

Fig12

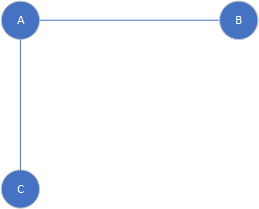
该子图关于母图Fig2的相对补图

Fig13

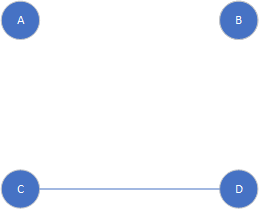
下面介绍一下完全图，完全图，简而言之，就是给定一个顶点集合，任意两个顶点之间都有边，比如对于ABCD来，他的完全图是这样的，对于更多顶点就会更加麻烦了。

Fig14

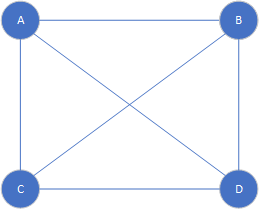
而实际上任意一个图都有补图，这个补图，是相对于它的完全图（严谨的说应该是它点集的完全图）的相对补图，

对于最开始的简单图ABCD来说它的补图其实就是这样的

Fig15

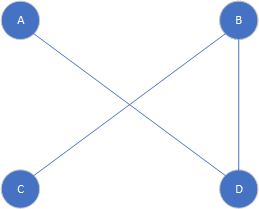
当然对于它的子图Fig12的补图，注意这里不是关于母图的相对补图了，是子图本身的补图，别弄混淆了，就

Fig16

权图

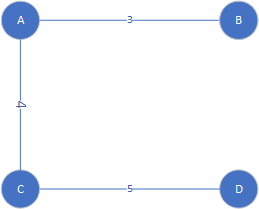
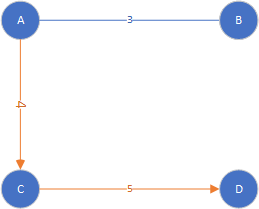
当我们要表示，城市间的距离的时候，我们可以再对应的边上加上一个实数，称为权值，用$\omega$表示。比如我们再简单图ABCD加上路径长度时，就可以表示成这样，显然 $\omega (AB)=3$，$\omega (AC)=4$

Fig17

但是如果两个顶点之间没有边的存在，我们就认为他们之间的权值（距离）为无穷大，比如$\omega (AD)=\infty$，有时候，我们可能用到顶点到自己的权值，所以我们规定$\omega (AA)=0$

路

路实际上是两个顶点之间的路径，用顶点序列来表示(实际上我觉得用边序列来表示也可以)，比如Fig17中的AD之间的路就表示为(A,C,D),实际上我们并没有规定每个顶点只走一次，所以(A,B,A,C,D)也算AD之间的路。下图是路(A,C,D)

FIg18

要是只走一次呢，就称为简单路（但是端点可以相同,所以(A,B,A)也算简单路），所以(A,C,D)是简单路，(A,B,A,C,D)不是简单路.

注意路中的顶点序列是相邻的，相邻即，在序列中，连续的两个顶点需作为同一条边的端点，比如顶点A和C相邻，A和D不相邻

最短路径

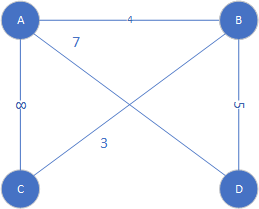
两个端点之间可能有多条路，比如下图AC之间有(A,C),(A,B,C),(A,D,C)等路径，其中路径上的边权值和最小的称为最短路径，经计算，AC之间最短路径是也刚好是(A,B,C)（有时候可能绕个弯却会更短），且路径长度为7，我们称这个AC最短路径长度为AC之间的距离，记为 $d(A,C)=7$

Fig19

Dijkstra算法

我们再上面使用的计算最短路径的方法是枚举法，就是简单地举出所有路径，并计算长度，当图的规模变大了，比如包含几百个顶点，几万条边，这个方法就不靠谱了。下面介绍Dijkstra算法。

首先我们在最短路径那里定义了点之间的距离，下面引入点与点集合之间的距离，如下图所示，当整个图的点集$G$为 { A , B , C , D } \{A,B,C,D\} {A,B,C,D}时，比如有一个点集合 S = { B , D } S=\{B,D\} S={B,D}，一个点为$A$，我们定义$A$到$S$的距离,为$A$到$S$中的每一点$v$的距离最小值，记作 d ( A , S ) = min ⁡ v ∈ S { d ( A , v ) } d(A,S)=\min\limits_{v\in S}\{d(A,v)\} d(A,S)=v∈Smin​{d(A,v)},显然 d ( A , S ) = min ⁡ { d ( A , B ) , d ( A , D ) } d(A,S)=\min\{d(A,B),d(A,D)\} d(A,S)=min{d(A,B),d(A,D)}

Fig20

我们可以在$S^{\prime }=G-S$中找到一点$u$(可以是$A$本身), 使得 d ( A , S ) = min ⁡ v ∈ S { d ( A , v ) } = min ⁡ v ∈ S u ∈ S ′ { d ( A , u ) + ω ( u , v ) } d(A,S)=\min\limits_{v\in S}\{d(A,v)\}=\min\limits_{v\in S\\u\in S'}\{d(A,u)+\omega(u,v)\} d(A,S)=v∈Smin​{d(A,v)}=v∈Su∈S′min​{d(A,u)+ω(u,v)}

所以可以有如下组合

当$u=A$时,$d(A,A)=0$,$\omega (A,B)=4$,$\omega (A,D)=7$,所以

min ⁡ u ∈ S ′ { d ( A , u ) + ω ( u , v ) } = min ⁡ { d ( A , A ) + ω ( A , B ) , d ( A , A ) + ω ( A , D ) } = min ⁡ { 0 + 4 , 0 + 7 } = 4 \min\limits_{u\in S'}\{d(A,u)+\omega(u,v)\}=\min\{d(A,A)+\omega(A,B),d(A,A)+\omega(A,D)\}=\min\{0+4,0+7\}=4 u∈S′min​{d(A,u)+ω(u,v)}=min{d(A,A)+ω(A,B),d(A,A)+ω(A,D)}=min{0+4,0+7}=4

当$u=C$时,$d(A,C)=8$,$\omega (C,B)=3$,$\omega (C,D)=\infty$（这里不是距离,而是边的权值)，有

min ⁡ u ∈ S ′ { d ( A , u ) + ω ( u , v ) } = min ⁡ { d ( A , C ) + ω ( C , B ) , d ( A , C ) + ω ( C , D ) } = min ⁡ { 8 + 3 , 8 + ∞ } = 11 \min\limits_{u\in S'}\{d(A,u)+\omega(u,v)\}=\min\{d(A,C)+\omega(C,B),d(A,C)+\omega(C,D)\}=\min\{8+3,8+\infty\}=11 u∈S′min​{d(A,u)+ω(u,v)}=min{d(A,C)+ω(C,B),d(A,C)+ω(C,D)}=min{8+3,8+∞}=11

综上所述

d ( A , S ) = min ⁡ v ∈ S u ∈ S ′ { d ( A , u ) + ω ( u , v ) } = 4 d(A,S)=\min\limits_{v\in S\\u\in S'}\{d(A,u)+\omega(u,v)\}=4 d(A,S)=v∈Su∈S′min​{d(A,u)+ω(u,v)}=4

其实从这里就可以看到Dijkstra的影子了，下面给出简单版本算法

目标：求给定点$u_0$到图中各点的最短距离（亦称单源最短路径）

1.初始化 S ′ = { u 0 } S'=\{u_0\} S′={u0​}，给定点集$S=P-S^{\prime }$,对于$S$中的每一点$v$,令$d(u_0,v)=d(u_0,u_0)+\omega (u_0,v)$(显然这里的$u=u_0$)

2.找出$u_0$到$S$的最短距离，并确定该点$u_i$，即在S中找出一点$u_i$使得$d(u_0,u_i)$最小，用公式表示为

​ d ( u 0 , u i ) = min ⁡ v ∈ S { d ( u 0 , v ) } d(u_0,u_i)=\min\limits_{v\in S}\{d(u_0,v)\} d(u0​,ui​)=v∈Smin​{d(u0​,v)}

3.若$S\ne P$,从给定点集S中删除$u_i$,并将其加入到$S^{\prime }$中，用公式表示为 S = S − { u i } , S ′ = S ′ ∪ { u i } S=S-\{u_i\},S'=S'\cup\{u_i\} S=S−{ui​},S′=S′∪{ui​}

​ 否则当$S=P$时，则终止

4.对于新的S中的每一个点$v$,重新计算 d ( u 0 , v ) = min ⁡ u ∈ S ′ { d ( u 0 , u ) + ω ( u , v ) } d(u_0,v)=\min\limits_{u\in S'}\{d(u_0,u)+\omega(u,v)\} d(u0​,v)=u∈S′min​{d(u0​,u)+ω(u,v)}

其实上面基本能用了，但是还有一些地方可以优化的

其一,对于二维数组$d(u,v)$实际上我们只使用了$d(u_0,v)$,所以可以将它优化成一维数组$d(v)$

再者，第4步，重新计算 d ( u 0 , v ) = min ⁡ u ∈ S ′ { d ( u 0 , u ) + ω ( u , v ) } d(u_0,v)=\min\limits_{u\in S'}\{d(u_0,u)+\omega(u,v)\} d(u0​,v)=u∈S′min​{d(u0​,u)+ω(u,v)}的时候有很多重复计算，让我们看看那里出来的重复计算？

当 S ′ = { u 0 , u 1 , . . . u i } S'=\{u_0,u_1,...u_i\} S′={u0​,u1​,...ui​}时，

d ( u 0 , v ) = min ⁡ u ∈ S ′ { d ( u 0 , u ) + ω ( u , v ) } = min ⁡ { d ( u 0 , u 0 ) + ω ( u 0 , v ) , d ( u 0 , u 1 ) + ω ( u 1 , v ) , . . . , d ( u 0 , u i ) + ω ( u i , v ) } d(u_0,v)\\=\min\limits_{u\in S'}\{d(u_0,u)+\omega(u,v)\}\\=\min\{d(u_0,u_0)+\omega(u_0,v),d(u_0,u_1)+\omega(u_1,v),...,d(u_0,u_i)+\omega(u_i,v)\} d(u0​,v)=u∈S′min​{d(u0​,u)+ω(u,v)}=min{d(u0​,u0​)+ω(u0​,v),d(u0​,u1​)+ω(u1​,v),...,d(u0​,ui​)+ω(ui​,v)}

当 S ′ = { u 0 , u 1 , . . . u i , u i + 1 } S'=\{u_0,u_1,...u_i,u_{i+1}\} S′={u0​,u1​,...ui​,ui+1​}时，

d ( u 0 , v ) = min ⁡ u ∈ S ′ { d ( u 0 , u ) + ω ( u , v ) } = min ⁡ { d ( u 0 , u 0 ) + ω ( u 0 , v ) , d ( u 0 , u 1 ) + + ω ( u 1 , v ) . . . , d ( u 0 , u i ) + ω ( u i , v ) , d ( u 0 , u i + 1 ) + ω ( u i + 1 , v ) } d(u_0,v)\\=\min\limits_{u\in S'}\{d(u_0,u)+\omega(u,v)\}\\=\min\{d(u_0,u_0)+\omega(u_0,v),d(u_0,u_1)++\omega(u_1,v)...,d(u_0,u_i)+\omega(u_i,v),d(u_0,u_{i+1})+\omega(u_{i+1},v)\} d(u0​,v)=u∈S′min​{d(u0​,u)+ω(u,v)}=min{d(u0​,u0​)+ω(u0​,v),d(u0​,u1​)++ω(u1​,v)...,d(u0​,ui​)+ω(ui​,v),d(u0​,ui+1​)+ω(ui+1​,v)}

我们可以发现，在计算S’= { u 0 , u 1 , . . . . u i + 1 } \{u_0,u_1,....u_{i+1}\} {u0​,u1​,....ui+1​}最小值的时候，又计算了一遍在 { u 0 , u 1 , . . . . u i } \{u_0,u_1,....u_i\} {u0​,u1​,....ui​}中的最小值，其实已经保存了 { u 0 , u 1 , . . . . u i } \{u_0,u_1,....u_i\} {u0​,u1​,....ui​}的最小值，就直接和$u_i$对应的值比较就行了。

就优化成这样

d ( u 0 , v ) = min ⁡ u ∈ S ′ { d ( u 0 , u ) + ω ( u , v ) } = min ⁡ { d ( u 0 , v ) , d ( u 0 , u i + 1 ) + ω ( u i + 1 , v ) } d(u_0,v)\\=\min\limits_{u\in S'}\{d(u_0,u)+\omega(u,v)\}\\=\min\{d(u_0,v),d(u_0,u_{i+1})+\omega(u_{i+1},v)\} d(u0​,v)=u∈S′min​{d(u0​,u)+ω(u,v)}=min{d(u0​,v),d(u0​,ui+1​)+ω(ui+1​,v)}

结合前面两个优化，最后的Dijkstra算法如下

1.初始化 S ′ = { u 0 } S'=\{u_0\} S′={u0​}，给定点集$S=P-S^{\prime }$,对于$S$中的每一点$v$,令$d(v)=d(u_0)+\omega (u_0,v)$(显然这里的$u=u_0$)

2.找出$u_0$到$S$的最短距离，并确定该点$u_i$，即在S中找出一点$u_i$使得$d(u_i)$最小，用公式表示为

​ d ( u i ) = min ⁡ v ∈ S { d ( v ) } d(u_i)=\min\limits_{v\in S}\{d(v)\} d(ui​)=v∈Smin​{d(v)}

3.若$S\ne P$,从给定点集S中删除$u_i$,并将其加入到$S^{\prime }$中，用公式表示为 S = S − { u i } , S ′ = S ′ ∪ { u i } S=S-\{u_i\},S'=S'\cup\{u_i\} S=S−{ui​},S′=S′∪{ui​}

​ 否则当$S=P$时，则终止

4.对于新的S中的每一个点$v$,重新计算 d ( v ) = min ⁡ u ∈ S ′ { d ( u ) + ω ( u , v ) } d(v)=\min\limits_{u\in S'}\{d(u)+\omega(u,v)\} d(v)=u∈S′min​{d(u)+ω(u,v)}

当然其中$d(u_0)=0$,是可以省略的

关于证明：

证明这条路径时最小的，其实考虑三个方面（路径第一步进入S，路径最后一步进入S，路径中间某步进入S），简单放缩一下，具体参考课本