leetcode 动态规划学习一

最新推荐文章于 2024-05-28 21:13:10 发布

春暖夏凉

最新推荐文章于 2024-05-28 21:13:10 发布

阅读量170

点赞数

分类专栏： leetcode 文章标签： c++

本文链接：https://blog.csdn.net/weixin_42808534/article/details/105968637

版权

leetcode 专栏收录该内容

13 篇文章 0 订阅

订阅专栏

基本概念

动态规划 问题一般就是求最值，比如最长上升子序列。最小编辑距等等 ，其**核心思想是穷举**，要求最值肯定把所有情况进行穷举。
直接穷举会超时，动态规划问题存在[重叠问题]，如果暴力效率低下的话，可以采用 [备忘录] 和[DP table] 来优化穷举过程。
虽然一定存在最优子结构 ，但是**关键点在找出状态转移方程**
明确【状态】-> 明确dp 数组含义-> 明确【选择】->确定【base case】

1、斐波那契数列问题
在这里插入图片描述

（1）普通递归每次都需要重复计算含有大量重复计算问题

  int fib(int N) {
        //1 1 2 3 5 8 
        if(N==1||N==2)  return 1; 
        //cout<<fib(N-1)+fib(N-2)<< " ;";
        return fib(N-1)+fib(N-2);
    }

（2）带备忘录的递归
每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了

class Solution {
public:
    int fib(int N) {
        if(N<1)  return 0;
        vector<int> memo(N+1,0);
        return helper(memo,N);
    }
    int helper(vector<int> &memo, int n)
    {
        if(n==1||n==2) return 1;
        // 如果以前计算过 计算过直接返回值 不用再次计算
        if(memo[n]!=0) return memo[n];
        memo[n]=helper(memo,n-1)+helper(memo,n-2);
        return memo[n];
    }
};

ps 理解一下 递归条**用函数栈**困扰了好久的
函数栈：栈里面每一层都是装的都是函数的栈就是函数栈，调用一个函数的时候，这个函数就入栈，这个函数调用完成了（执行到了函数的最后一个语句或者说return了），就出栈。
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200507140045237.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MjgwODUzNA==,size_16,color_FFFFFF,t_70)

自己调用自己
递归通常不在意具体操作，只关心初始条件和上下层的变化关系。
递归函数需要有临界停止点，即递归不能无限制的执行下去。通常这个点为必须经过的一个数。
递归通常能被其他方案替代(栈、数组正向求)。
在这里插入图片描述

啥叫「自顶向下」？注意我们刚才画的递归树（或者说图），是从上向下延伸，都是从一个规模较大的原问题比如说f(20)，向下逐渐分解规模，直到f(1)和f(2)触底，然后逐层返回答案，这就叫「自顶向下」。

啥叫「自底向上」？反过来，我们直接从最底下，最简单，问题规模最小的f(1)和f(2)开始往上推，直到推到我们想要的答案f(20)，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算
3 、DP迭代解法
有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算岂不美哉
在这里插入图片描述

画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。

凑零钱问题

暴力递归

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        // 看作回溯 dfs 的跳出条件
        if(amount == 0){
            return 0;
        }

        // 找一个流程 
        //硬币数量
        int result = INT_MAX;
        // for循环会列举每次合适的情况不会遗漏 也不会重复
        for(int coin : coins)
        {   
            //为了后续 一开始肯定不会出现这种情况 算是剪枝吗 ？
            // 改成判断amount>coin 也行
            if(amount - coin < 0)
            {
                //当前所需金额小于零钱,跳过,尝试下一种零钱
                continue;
            }
            //递归中间结果
            int subResult = coinChange(coins,amount - coin);
            //子问题无解

            if(subResult == -1)
            {
                continue;
            }
            //找出最优子结构

            // 子问题 +1  与此次选取结果比较 选取一个最小的 
            result = min(subResult + 1,result);
        }
         
        //子问题返回值 
        return result == INT_MAX ? -1 : result;  
    }
};

如何列出正确的状态转移方程。
想求amount = 11时的最少硬币数（原问题），如果你知道凑出amount = 10的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1 的硬币）就是原问题的答案，因为硬币的数量是没有限制的，子问题之间没有相互制，是互相独立的
先确定「状态」，也就是原问题和子问题中变化的变量。由于硬币数量无限，所以唯一的状态就是目标金额amount。

然后确定dp函数的定义：函数 dp(n)表示，当前的目标金额是n，至少需要dp(n)个硬币凑出该金额。
然后确定「选择」并择优，也就是对于每个状态，可以做出什么选择改变当前状态。具体到这个问题，无论当的目标金额是多少，选择就是从面额列表coins中选择一个硬币，然后目标金额就会减少：

# 伪码框架
def coinChange(coins: List[int], amount: int):
    # 定义：要凑出金额 n，至少要 dp(n) 个硬币
    def dp(n):
        # 做选择，需要硬币最少的那个结果就是答案
        for coin in coins:
            res = min(res, 1 + dp(n - coin))
        return res
    # 我们要求目标金额是 amount
    return dp(amount)

def coinChange(coins: List[int], amount: int):

    def dp(n):
        # base case
        if n == 0: return 0
        if n < 0: return -1
        # 求最小值，所以初始化为正无穷
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            # 子问题无解，跳过
            if subproblem == -1: continue
            res = min(res, 1 + subproblem)

        return res if res != float('INF') else -1

    return dp(amount)

状态转移方程
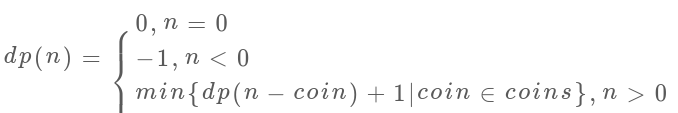
在这里插入图片描述

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
         // 改成动态规划 
         //dp[i] 表示 凑成i所需要的 最少硬币数量为 dp[i];
        vector<int> dp(amount+1,amount+1);
        dp[0]=0;
        //dp[1]=1;
        for(int i=1;i<=amount;i++)
        {
         for(auto coi: coins)
         {
            if(i<coi) continue;
            dp[i]=min(dp[i],1+dp[i-coi]);  // 初始化INT_MAX 会越界
         }
        }
        return (dp[amount]==amount+1) ? -1 :dp[amount];
    }
};

爬台阶问题（等同于斐波那契数列）

#动态规划方法

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n+1,0);
        // dp[i]  表示爬到底i层有dp[i] 中方法
        if(n==1||n==2) return n;
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

不同路径问题

在这里插入图片描述

动太规划代码

class Solution {
public:

    int uniquePaths(int m, int n) {
        // m 列  你行
        vector<vector<int>> dp(n+1,vector<int>(m+1,0));
            for(int i=1;i<=n;i++)
            {
                for(int j=1;j<=m;j++)
                {
                    if(i==1||j==1)
                    {
                        dp[i][j]=1;

                    }else {
                         // 状态转移方程
                        dp[i][j]=dp[i][j-1]+dp[i-1][j];
                    }
                }
            }
        
        return dp[n][m];
    }
};

记忆化递归

class Solution {
public:

     vector<vector<int>> a;
    int uniquePaths(int m, int n) {
        a=vector<vector<int>> (m,vector<int>(n,0));
        return heip(m-1,n-1);
    }

    int heip(int m ,int n)
    {
        if(m<0||n<0)  return 0;
        if(m==0||n==0)  return 1;    // 参数调用的时候 已经-1 le 
        if(a[m][n]>0)  return a[m][n];  // >0 代表已经计算过
        a[m][n]=heip(m-1,n)+heip(m,n-1);
        return a[m][n];

    }
};



    /**
     * 【记忆化搜索】
     * @param m
     * @param n
     * @return
     */
    public int uniquePaths3(int m ,int n){
        int[][] dp = new int[m + 1][n + 1];
        return uniquePaths2(m,n,dp);
    }
    public int uniquePaths2(int m,int n,int[][] dp){
        if(m <= 0 || n <= 0){
            return 0;
        }
        //只有一行或者只有一列，只能不断向右或者不断向下
        if(m == 1 || n == 1){
            return 1;
        }
        //两行两列
        if(m == 2 && n == 2){
            return 2;
        }
        //两行三列或者三行两列
        if(( m == 2 && n == 3 )||( m == 3 && n == 2 )){
            return 3;
        }
        if(dp[m][n] > 0){
            return dp[m][n];
        }
        //向右的所有路径
        dp[m - 1][n] = uniquePaths2(m - 1,n,dp);
        //向下的所有路径
        dp[m][n - 1] = uniquePaths2(m,n - 1,dp);
        dp[m][n] = dp[m][n -1] + dp[m - 1][n];
        return dp[m][n];
    }

暴力递归

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m<=0||n<=0) {
            return 0;
        }

        // 只有一行或者一列的情况下
        if(m==1||n==1) 
        {
            return 1;
        }

        if(n==2&&m==2)
        {
            return 2;
        }

        if((m==2&&n==3)||(m==3&&n==2))
        {
            return 3;
        }
        int paths=0;
        //向右的所有路径
        paths+=uniquePaths(m-1,n);
        // 向左的所有路
        paths+=uniquePaths(m,n-1);

        return paths;
    }
};

不同路径Ⅱ

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid.empty()||obstacleGrid[0].empty())  return 0;
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();

        vector<vector<int>> dp(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(obstacleGrid[i][j]==1)
                {
                    dp[i][j]=0;
                }else {
                    // 排除 i-1  j- 小于0 的情况
                    if(i==0&&j==0) dp[i][j]=1;
                    else  if(i==0)  dp[i][j]=dp[i][j-1];
                    else  if(j==0)  dp[i][j]=dp[i-1][j];
                    else dp[i][j]=dp[i-1][j]+dp[i][j-1];

                }
            }
        }

        return dp[m-1][n-1];

    }
};

春暖夏凉

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
leetcode 动态规划学习一

基本概念动态规划问题一般就是求最值，比如最长上升子序列。最小编辑距等等，其**核心思想是穷举**，要求最值肯定把所有情况进行穷举。直接穷举会超时，动态规划问题存在[重叠问题]，如果暴力效率低下的话，可以采用 [备忘录] 和[DP table] 来优化穷举过程。虽然一定存在最优子结构，但是**关键点在找出状态转移方程**明确【状态】-> 明确dp 数组含义-> 明确【选择】...
复制链接

扫一扫