LeetCode笔记|动态规划

最新推荐文章于 2024-05-20 21:56:33 发布

daydreamer_000

最新推荐文章于 2024-05-20 21:56:33 发布

阅读量98

点赞数

文章标签： leetcode 算法职场和发展 Powered by 金山文档

本文链接：https://blog.csdn.net/weixin_42860453/article/details/129776490

版权

知识点：

动态规划

参考文章：

(3条消息) 动态规划详解_Meiko丶的博客-CSDN博客

(3条消息) 教你彻底学会动态规划——入门篇_ChrisYoung1314的博客-CSDN博客

什么是动态规划？

通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常适用于有重叠子问题和最优子结构性质的问题。

动态规划核心思想：

拆分子问题，记住过往，减少重复计算

动态规划问题解题思路：

将原问题分解为若干子问题

确定状态

确定初始状态（边界状态）的值

确定状态转移方程

能用动态规划解决的问题的特点：

①问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，则称该问题具有最优子结构性质。

②无后效性。当前的若干状态值一旦确定，则此后过程的演变就只和这个若干状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态无关。

递归到动态规划的一般转化方法：

递归函数有n个参数，就定义一个n维数组，数组的下标是递归函数参数的取值范围，数组元素的值是递归函数的返回值，这样就可以从边界值开始，逐步填充数组，相当于计算递归函数的逆过程。

简单题型：

剑指offer 10 - Ⅱ.青蛙跳台阶问题

题目链接：剑指 Offer 10- II. 青蛙跳台阶问题 - 力扣（LeetCode）

解题思路：

f(n) = f(n-1) + f(n-2)

可以转化为求斐波那契数列第n项值

剑指 Offer 10- I. 斐波那契数列 - 力扣（LeetCode）

斐波那契数列解法：

方法一：动态规划

使用【滚动数组】的方法优化空间复杂度

用a代表n-2，b代表n-1，sum=a+b

之后令a=b，b=sum，再通过sum=a+b，可以计算出新的sum值

取模运算的运算法则（取模解决“指数爆炸”）：

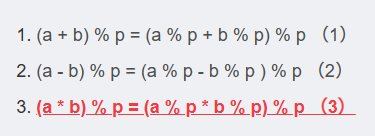
class Solution {
public:
    int fib(int n) {

        int sum, a = 0, b = 1; //初始化三个变量，a初始为f0，b初始为f1
        if(n == 0)  return 0; //判断边界0
        if(n == 1)  return 1; //判断边界1
        for(int i = 0; i < n - 1; i++) {
            sum = (a + b) % 1000000007; //取模
            a = b;
            b = sum;
        }
        return sum;
    }
};

时间复杂度：O(n)

空间复杂度：O(1)

方法二：矩阵快速幂

降低时间复杂度到O(logn)

快速幂算法

(8条消息) 快速幂算法（全网最详细地带你从零开始一步一步优化）_刘扬俊的博客-CSDN博客

取模运算的运算法则：

核心思想：

每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。

最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。

快速幂运算代码如下

long long fastPower(long long base, long long power) {
    long long result = 1;
    while (power > 0) {
        if (power & 1) {//此处等价于if(power%2==1) 位运算
            result = result * base % 1000;
        }
        power >>= 1;//此处等价于power=power/2
        base = (base * base) % 1000;
    }
    return result;
}

则对于本题，定义矩阵快速幂运算

class Solution {
public:
    const int MOD = 1000000007;

    int fib(int n) {
        if (n < 2) {
            return n;
        }
        vector<vector<long>> q{{1, 1}, {1, 0}};
        vector<vector<long>> res = pow(q, n - 1);
        return res[0][0];
    }

    //矩阵的快速幂运算
    vector<vector<long>> pow(vector<vector<long>>& a, int n) {
        vector<vector<long>> ret{{1, 0}, {0, 1}};
        while (n > 0) {
            if (n & 1) { //位运算 等价于if(n%2==1) 奇数
                ret = multiply(ret, a);
            }
            n >>= 1; //等价于n=n/2
            a = multiply(a, a);
        }
        return ret;
    }

    //定义矩阵乘法
    vector<vector<long>> multiply(vector<vector<long>>& a, vector<vector<long>>& b) {
        vector<vector<long>> c{{0, 0}, {0, 0}};
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
            }
        }
        return c;
    }
};

青蛙跳台阶问题动态规划解法：

class Solution {
public:
    int numWays(int n) {
        int sum, a = 1, b = 2; //a初始为f1，b初始为f2
        if (n == 0) return 1;
        if (n <= 2) return n;
        for (int i = 1; i < n - 1; i++) {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
        }
        return sum % 1000000007;

    }
};

相同题目还有：70. 爬楼梯 - 力扣（LeetCode）

例题：300. 最长递增子序列 - 力扣（LeetCode）

方法一：动态查找

思路：

用dp[i]记录以第i个数组结尾的最长上升子序列的长度（num[i]必须被选取）

在求dp[i]时，0 到 i-1的dp值已经算出来了

dp[i]就等于nums[j]小于nums[i]的最大dp[j]+1

即状态转移方程为：

dp[i]=max(dp[j])+1,其中0≤j<i且num[j]<num[i]

时间复杂度： O(n2)

空间复杂度：O(n)

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp; //dp数组存储以当前i下标元素nums[i]结尾的最长严格递增子序列长度
        int iDp = 1; //当前dp值
        int max = 1; //最大值
        dp.push_back(1); //第一个为1
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]) {
                    if(iDp < dp[j] + 1)   iDp = dp[j] + 1;
                }        
            }
            dp.push_back(iDp);
            if(max < iDp)   max = iDp;
            iDp = 1;
        }
        return max;
    }
};

方法二：贪心+二分查找

知识点：贪心算法

(2条消息) 贪心算法（greedy algorithm，又称贪婪算法）详解（附例题）_Kk.巴扎嘿的博客-CSDN博客

(2条消息) 从零开始学贪心算法_houjingyi233的博客-CSDN博客

(2条消息) 贪心算法(贪婪算法)_一个软泥怪的博客-CSDN博客

概念：

1.贪心算法又叫登山算法，根本思想是逐步获得最优解。在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，它所做出的是在某种意义上的局部最优解。

2.算法设计的关键是贪婪策略的选择。贪心策略要无后向性，也就是说某状态以后的过程不会影响以前的状态，只与当前状态有关。

3.贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。

局部最优并不总能获得整体最优解，但通常能获得近似最优解。

4.问题的最优子结构性质是该问题可用贪心算法求解的关键特征。

5.贪心算法的基本思路：

从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，它的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。

6.该算法存在的问题

①不能保证求得的最后解是最佳的

②不能用来求最大值或最小值的问题

③只能求满足某些约束条件的可行解的范围

7.贪心算法的步骤

①建立数学模型来描述问题

②把求解的问题分成若干子问题

③对每个子问题求解，得到子问题的局部最优解

④把子问题的局部最优解结合成原来问题的一个解

8.贪心算法是动态规划的一个特例，不需要自底向上遍历空间树，只需要从根开始，选择最优的路，一直走到底。

9.求解时应考虑的问题：

①候选集合C

为构造问题的解决方案，有一个候选集合C作为问题的可能解，问题的最终解均取自于候选集合C

②解集合S

随着贪心选择的进行，解集合不断扩展，直到构成一个满足问题的完整解

③解决函数solution

检查解集合是否构成问题的完整解

④选择函数select

即贪心策略，贪心算法的关键，指出哪个候选对象有希望构成问题的解

⑤可行函数feasible

检查解集合中加入一个候选对象是否可行，即解集合扩展后是否满足约束条件

贪心例题：

860. 柠檬水找零 - 力扣（LeetCode）

直接解：

（这里使用的贪心策略就是对于面额20的优先找回面额10+5的）

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int countFive = 0, countTen = 0; //记录现有的5.10张数
        for (int i = 0; i < bills.size(); i++) {
            if (bills[i] == 5)  countFive++;
            else if(bills[i] == 10) {
                countTen++;
                if (countFive > 0)  countFive--;
                else    return false;
            }else {
                if (countFive > 0 && countTen > 0) {
                    countFive--;
                    countTen--;
                }
                else if (countFive >= 3)    countFive -= 3;
                else    return false;
            }
        }
        return true;

    }
};

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

先做一下121题：

121. 买卖股票的最佳时机 - 力扣（LeetCode）

暴力解法（会超时）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int maxPro = 0; //最大利润
        for (int i = 0; i < prices.size() - 1; i++) {
            for (int j = i+1; j < prices.size(); j++) {
                if(prices[j] > prices[i])
                    maxPro = max(maxPro, prices[j] - prices[i]);
            }
        }
        return maxPro;

    }
};

动态规划一次遍历

遍历一次数组，用minPrice存储当前的最小元素（因为如果再有价格上升，也是目前的最小值买入可以获得更大利润），后续遍历的元素，如果比minPrice大，则将其差值与maxProfit比较，若大于maxProfit，则可更新当前值为maxProfit的值；如果后续遍历的元素有比minPrice小的，则更新当前元素为minPrice。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int min_Price = prices[0] , max_Profit = 0;
        for (int i = 1; i < prices.size(); i++) {
            if (prices[i] - min_Price > max_Profit)
                max_Profit = prices[i] - min_Price;
            if (prices[i] < min_Price) 
                min_Price = prices[i];            
        }
        return max_Profit;
    }
};

再看122题：

方法一：贪心算法一次遍历

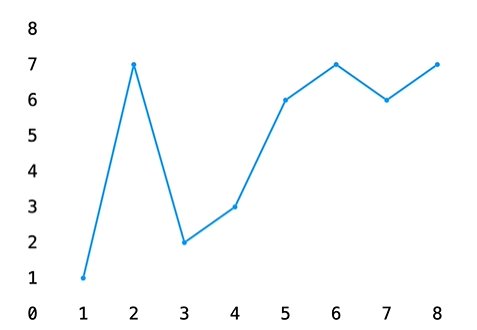
若第i+1天的价格比第i天高，就将其差值累加（画个图即可理解）

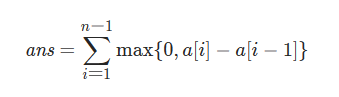
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int sum = 0;
        for (int i = 0; i < prices.size() - 1; i++) {
            if (prices[i+1] > prices[i]) {
                sum += prices[i+1] - prices[i];
            }
        }
        return sum;

    }
};

方法二：动态规划

用二维数组dp[ i ][ j ]定义状态

代表在第i天时，持股状态为j时，手上拥有的最大现金数

当j为0时，代表持有现金；当j为1时，代表持有股票

初始状态时，dp[ 0 ][ 0] = 0，代表不买股票

dp[ 0 ][ 1 ] = -prices[ 0 ]，即当前股票价格的负数

向后遍历，分别存储该天持有现金和持有股票的最大现金数

对于持有现金的最大现金数，即dp[ i ][ 0 ]：

可能的状态是:

前一天已经未持有股票，即dp[ i - 1 ][ 0 ]

或者前一天持有股票该天卖出，即dp[ i - 1 ][ 1 ] + prices[ i ]

对于持有股票的最大现金数，即dp[ i ][ 1 ]

取两者中的最大值

可能的状态是：

前一天已持有股票，即dp[ i - 1 ][ 1 ]

或者前一天未持有股票该天买入，即dp[ i - 1 ][ 0 ] - prices[ i ]

取两者中的最大值

最后返回最后一天未持有股票的最大现金数，即dp[ len - 1 ][ 0 ]

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int dp[3*10000][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[prices.size() - 1][0];

    }
};

优化空间：

既然都只与前一天的dp值有关

则用两个值存储第i-1天的两种情况下的最大现金数即可

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int iCash = 0, iStock = -prices[0];
        for(int i = 1; i < prices.size(); i++) {
            int tempCash = iCash, tempStock = iStock;
            iCash = max(tempCash, tempStock + prices[i]);
            iStock = max(tempStock, tempCash - prices[i]);
        }
        return iCash;

    }
};

123. 买卖股票的最佳时机 III - 力扣（LeetCode）

解题思路：

分为五种状态：未操作；买一次；买一次后卖一次；买二次；买二次后卖二次

其中未操作状态可以不计入

用buy1, sell1, buy2, sell2 代表上述状态

对于buy1，买一次的状态，可能是上一天已经买一次，即buy1，或者上一天未操作，该天买入，为-prices[ i ]，取两者最大值。

对于sell1，上一天买入一次，当天卖出，即buy1 + prices[ i ]，或者上一天已经卖出，即sell1，取两者最大值。

对于buy2，买两次的状态，上一天已经卖出第一支，当天再买入，即sell1 - prices[ i ]，或者上一天已经买入二次，即buy2，取两者最大值。

对于sell2，卖出第二支，则为buy2 + prices[ i ]或sell2，取两者最大值。

最后取sell2和sell1的最大值，因为有可能只买卖一次

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int buy1 = -prices[0], sell1 = 0, buy2 = -prices[0], sell2 = 0;
        for (int i = 1; i < prices.size(); i++) {
            int tempBuy1 = buy1, tempBuy2 = buy2, tempSell1 = sell1, tempSell2 = sell2;
            buy1 = max(tempBuy1, -prices[i]);
            sell1 = max(tempSell1, tempBuy1 + prices[i]);
            buy2 = max(tempBuy2, tempSell1 - prices[i]);
            sell2 = max(tempSell2, tempBuy2 + prices[i]);
        }
        return max(sell2, sell1);
    }
};

188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

解题思路：

同上一题，只需要把上题的两个buy和sell，定义为大小为k的数组即可

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        //定义一个数组，下标表示买卖n+1次
        int buy[k], sell[k], tempBuy[k], tempSell[k];
        for (int i = 0; i < k; i++) {
            buy[i] = -prices[0];
            sell[i] = 0;
        }

        for (int i = 1; i < prices.size(); i++) {

            tempBuy[0] = buy[0];
            tempSell[0] = sell[0];
            buy[0] = max(tempBuy[0], -prices[i]);
            sell[0] = max(tempSell[0], tempBuy[0] + prices[i]);

            for (int j = 1; j < k; j++) {
                tempBuy[j] = buy[j];
                tempSell[j] = sell[j];
                buy[j] = max(tempBuy[j], tempSell[j - 1] - prices[i]);
                sell[j] = max(tempSell[j], tempBuy[j] + prices[i]);
            }

        }

        int maxSell = sell[0];
        //返回数组sell中的最大值
        for (int i = 1; i < k; i++) {
            maxSell = max(maxSell, sell[i]);
        }
        return maxSell;
    }
};

309. 最佳买卖股票时机含冷冻期 - 力扣（LeetCode）

解题思路：

可以将状态划分为“持有股票”和“不持有股票”，由于存在冷冻期，对于“不持有股票”的情况，有可能是处于冷冻期，也有可能不在冷冻期，所以分为三种状态，分别为dp[ i ][ 0 ], dp[ i ][ 1 ], dp[ i ][ 2 ]

对于dp[ i ][ 0 ]，当天持有股票，可以是前一天就持有股票，即dp[ i-1 ][ 0 ]，或者前一天没有股票，当天买入，此时前一天是“不持有股票，但不在冷冻期”，则为dp[ i-1 ][ 2 ] - prices[ i ]，取两者最大值。

对于dp[ i ][ 1 ]，当天不持有股票，且在冷冻期，则前一天一定持有股票且在当天卖出，即dp[ i-1 ][ 0 ] + prices[ i ]。

对于dp[ i ][ 2 ]，当天不持有股票，且不在冷冻期，则前一天就不持有股票，取dp[ i ][ 1 ]和dp[ i ][ 2 ] 的最大值。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int dp1 = -prices[0]; //持有股票
        int dp2 = 0; //不持有股票，且在冷冻期
        int dp3 = 0; //不持有股票，且不在冷冻期

        for (int i = 1; i < prices.size(); i++) {
            int tempDP1 = dp1, tempDP2 = dp2, tempDP3 = dp3;
            dp1 = max(tempDP1, tempDP3 - prices[i]);
            dp2 = tempDP1 + prices[i];
            dp3 = max(tempDP2, tempDP3);
        }

        return max(dp2, dp3);
    }

};

714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

解题思路：

分为“持有股票”和"不持有股票"两种状态，在买入股票时减去fee即可

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {

        int dpCash = 0, dpStock = -prices[0] - fee; //不持有股票和持有股票两种状态
        for (int i = 1; i < prices.size(); i++) {
            int tempCash = dpCash, tempStock = dpStock;
            dpCash = max(tempCash, tempStock + prices[i]);
            dpStock = max(tempStock, tempCash - prices[i] - fee);
        }
        return dpCash;

    }
};