小波变换图像处理-CSDN博客

本文链接：https://blog.csdn.net/weixin_42939683/article/details/107151247

小波

1 背景
2 快速小波变换
- 2.1 使用小波工具箱的FWT
- 2.2 不使用小波工具箱的FWT
3 小波分解结构的处理
4 图像中的小波

傅里叶变换是一种美丽的数学描述，但计算机实现是从时域和频域逐步离散的，傅里叶变换只显示信号或图像的频率特性，不提供任何时域信息。小波分析是最新的时频分析工具。与傅里叶变换相比，离散小波变换继承和发展了短时傅里叶变换的定位思想，克服了窗口大小不随频率变化的缺点。小波变换不仅在描述帧和多分辨率存储方面非常有效和直观，而且有助于深入了解图像的空间和频率特性。本文讨论了离散小波变换的计算和应用。首先介绍了小波工具箱。其次，研究了小波分解结构和快速逆小波变换。最后，将小波变换应用于边缘检测、图像平滑和渐进重构。实验结果表明，小波变换在图像处理中得到了广泛的应用。

小波（Wavelet），“小波”就是小区域，长度有限，均值为0的波形。所谓“小”是指它有衰减性，“波”指它具有波动性，其振幅正负相同的震荡形式。

1 背景

考虑大小为M×N的图像f(x,y)，这幅图像的正向离散变换T(u,v,…)可根据一般的关系来表示： $T(u,v,...)=\sum_{x,y}f(x,y)g_{u,v,...}(x,y)$ 在这里，x和y是空间变量，u,v,…是变换域变量。给定T(u,v,…)，f(x,y)可用一般的离散反变换得到： $f(x,y)=\sum_{u,v,...}T(u,v,...)h_{u,v,...}(x,y)$ g_u,v,…和h_u,v,…在这些方程中分别叫做正变换核和反变换核。他们决定其性质、计算的复杂性和变换对的主要用途。变换系数T(u,v,…)可以通过对f关于｛h_u,v,…｝的一系列展开系数来观察。也就是说，反变换核对于f的级数展开定义了一组展开函数。

在之前我们学过的离散傅里叶变换(DFT)能很好地适应级数展开公式。在这种情况下： $h_{u,v}(x,y)=g_{u,v}^*(x,y)=\frac{1}{\sqrt{MN}}e^{j2\pi (ux/M+vy/N)}$ 这里，j²=-1，*是复共轭算子，u=0,1,…,M-1且v=0,1,…,N-1。变换域变量u和v分别表示水平和垂直频率，变换核是可分的，因为： $h_{u,v}(x,y)=h_u(x)h_v(y)$ 对于 $h_u(x)=\frac{1}{\sqrt{M}}e^{j2\pi ux/M}$ 和 $h_v(y)=\frac{1}{\sqrt{N}}e^{j2\pi vy/N}$ 是正交的： $<h_r,h_s>=\delta_{rs}= \left\{\begin{matrix}1 \quad r=s \\ 0 \quad 其他 \end{matrix} \right.$ 其中，<>是内积算子。变换核的可分离性简化了二维变换的计算，可以用先作行后作列，或先作列后作行的一维变换来实现二维变换；归一化正交导致正反变换核之间的复共轭关系（如果函数是实数，他们相等）。

不像离散傅里叶变换，傅里叶变换完全可以通过两个简单的方程式来定义，这个方程式围绕变换核对循环出现，术语“离散小波变换”指的就是这样的一类变换，不仅使用的变换核不同，（所用的展开函数）而且这些函数（例如不管他们构成正交基还是双正交基）的基本性质和他们应用的方法也不同。因为DWT包含各种独特但相关的变换，所以我们不能写出单一的能完全描述他们的公式。取而代之，而是用变换核对或定义这些变换核对的一组参数来表征每个DWT。各种变换都与这样的事实有关，事实就是变换的展开函数是变化频率和持续时间受限的“小波”。在这一章的剩余部分，我们将介绍几种“小波”核，其中的每个都有下面的一般特性。

性质1： 可分离性，可伸缩性和平移性。变换核可用三个可分的二维小波来表示： $\psi^H(x,y)=\psi (x) \phi(y) \\ \psi^V(x,y)=\phi (x) \psi(y) \\ \psi^D(x,y)=\psi (x) \psi(y)$ 其中，ψ^H(x,y)、ψ^V(x,y)和ψ^D(x,y)分别被称为水平、垂直和对角小波，并且是二维可分的尺度函数： $\phi(x,y)=\phi(x)\phi(y)$ 每个二维函数都是两个一维实函数的、平方可积的尺寸和小波函数的乘积： $\phi_{j,k}(x)=2^{j/2}\phi(2^jx-k) \\ \psi_{j,k}(x)=2^{j/2}\psi(2^jx-k)$ 平移参数k决定这些一维函数沿x轴的位置，尺度j决定他们的宽度，它们沿x轴有多宽多窄，并且按2^j/2控制他们的高度或者振幅。注意，与展开函数相关联的是母小波的二进制尺度和整数平移ψ(x)=ψ_0,0(x)，并且尺度函数ϕ(x)=ϕ_0,0(x)。

性质2： 多分辨率的兼容性。刚刚介绍的一维尺度函数满足下面的多分辨率分析要求：
1）ϕ_j,k对整数平移是正交的。
2）在低尺度或低分辨率（例如较小的j）下，以一系列ϕ_j,k的展开函数来描述的一组函数包括在可以用高尺度描述的函数中。
3）唯一可在每个尺度上描述的函数是f(x)=0。
4）在j—>∞时，任何函数都可以以任意精度来描述。
在这些条件满足时，存在伴随小波ψ_j,k，与它的整数平移和二进制尺度一起，它的范围用任意两组ϕ_j,k之间的差来描述，ϕ_j,k是在相邻尺度上可描述的函数。

性质3： 正交性。对于一组一维可测的、平方可积函数，展开函数形成的正交或双正交基。之所以称为基，是因为对于每个可描述函数必须有唯一一组展开系数。正如在傅里叶核介绍中说明的那样，对于实数正交核，有g_u,v,…=h_u,v,…。对于双正交情况： $<h_r,g_s>=\delta_{rs}=\left\{\begin{matrix} 1 \quad r=s \\ 0 \quad 其他\end{matrix}\right.$ g被称为h的对偶。对于带有尺度和小波函数ψ_j,k和ϕ_j,k的双正交小波变换来说，对偶分别表示为ψ^~_j,k和ϕ^~_j,k。

2 快速小波变换

上述性质的重要推论是：ϕ(x)和ψ(x)可以用他们自身的双分辨率副本的线性组合来表达。这样，经过级数展开： $\phi(x)=\sum_nh_\phi(n)\sqrt{2}\phi(2x-n) \\ \psi(x)=\sum_nh_\psi(n)\sqrt{2}\phi(2x-n)$ 其中h_φ和h_Ψ分别称为尺度和小波矢量。

下图中对滤波器组的输入被分解为四个低分辨率(或低尺度)分量。Wφ系数是通过两个低通滤波器(即基于hφ的滤波器)产生的，因此称为近似系数；{W $φ^i$ for i=H，V，D}分别是水平的、垂直的和对角的细节系数。输出Wφ(j，m，n)可作为后续输入Wφ(j+1，m，n)，用于生成更低分辨率的分量；f(x，y)是可用的最高分辨率表示，可作为第一次迭代的输入。注意，下图中的运算既不使用小波，也不使用标度函数–只使用它们相关联的小波和标度向量。此外，还涉及三个变换域变量包括尺度j和水平和垂直平移，n和m。
在这里插入图片描述

2.1 使用小波工具箱的FWT

最古老和最简单的是基于Haar尺度和小波函数的小波变换。基于Haar变换的分解和重建滤波器的长度为2。

>> [Lo_D, Hi_D, Lo_R, Hi_R] = wfilters('haar')

Lo_D =
    0.7071    0.7071
Hi_D =
   -0.7071    0.7071
Lo_R =
    0.7071    0.7071
Hi_R =
    0.7071   -0.7071

它们的关键性质以及有关尺度和小波函数的平面图都可以得到：

>> waveinfo('haar');
 Information on Haar wavelet.
 
    Haar Wavelet
 
    General characteristics: Compactly supported 
    wavelet, the oldest and the simplest wavelet.
    
    scaling function phi = 1 on [0 1] and 0 otherwise.
    wavelet function psi = 1 on [0 0.5), = -1 on [0.5 1] and 0 otherwise.
 
    Family                  Haar
    Short name              haar
    Examples                haar is the same as db1
    Orthogonal              yes
    Biorthogonal            yes
    Compact support         yes
    DWT                     possible
    CWT                     possible
 
    Support width           1
    Filters length          2
    Regularity              haar is not continuous
    Symmetry                yes
    Number of vanishing 
    moments for psi         1
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 194-202.
>> [phi, psi, xval] = wavefun('haar', 10);
>> xaxis = zeros(size(xval));
>> subplot(1,2,1),plot(xval,phi,'k',xval,xaxis,'--k');
>> axis([0 1 -1.5 1.5]); axis square;
>> title('Haar Scaling Function');
>> subplot(1,2,2),plot(xval,psi,'k',xval,xaxis,'--k');
>> axis([0 1 -1.5 1.5]);axis square;
>> title('Haar Wavelet Function');

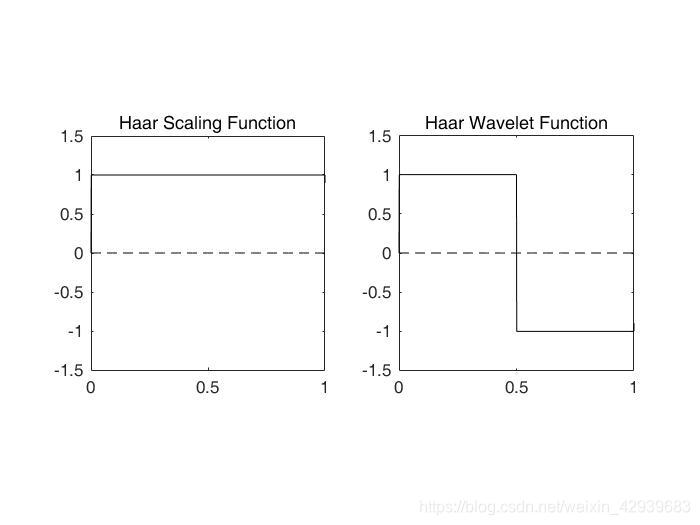
在这里插入图片描述
上图Haar标度函数和小波函数是不连续和紧支撑的，这意味着它们在一个称为支持的有限区间之外为0。另外，波形信息数据表明Haar展开函数是正交的，因此正变换核和逆变换核是一致的。下面我们使用Haar滤波器的简单FWT：

>> f = magic(4)

f =

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

>> [c1, s1] = wavedec2(f,1,'haar')

c1 =

  1 至 9 列

   17.0000   17.0000   17.0000   17.0000    1.0000   -1.0000   -1.0000    1.0000    4.0000

  10 至 16 列

   -4.0000   -4.0000    4.0000   10.0000    6.0000   -6.0000  -10.0000


s1 =

     2     2
     2     2
     4     4

在这里，一个4×4方形图像f被变换为16×16的小波分解向量c1和3×2的记录矩阵s1。整个变换由单独执行上一小节图中描述的操作来实现。4个2×2输出，分别是1个下取样近似和3个方向（水平、垂直和对角线）细节矩阵。wavedec2函数在行向量c1中以近似系数开始按列链接这些2×2矩阵，并且按水平、垂直和对角线细节逐一进行。也就是：c1(1)到c1(4)是近似系数W_φ(1,0,0)、W_φ(1,1,0)、W_φ(1,0,1)和W_φ(1,1,1)，任意假定的f的尺度为2；c1(5)到c1(8)是W_φ^H(1,0,0)、W_φ^H(1,1,0)、W_φ^H(1,0,1)、W_φ^H(1,1,1)等。如果从向量c1中提取水平细节矩阵，将得到： $W_\psi^H=\begin{bmatrix}1&-1 \\ -1 & 1\end{bmatrix}$ 当前面描述的单尺度变换扩展到两个尺度时，我们得到：

>> [c2, s2] = wavedec2(f,2,'haar')

c2 =

  1 至 9 列

   34.0000         0         0    0.0000    1.0000   -1.0000   -1.0000    1.0000    4.0000

  10 至 16 列

   -4.0000   -4.0000    4.0000   10.0000    6.0000   -6.0000  -10.0000


s2 =

     1     1
     1     1
     2     2
     4     4

注意，c2(5：16)=C1(5：16)。元素C1(1：4)是单尺度变换的近似系数，被输入图8.2的滤波器组，产生四个1X1输出：Wφ(O，0，0)， $w_Ψ$ H(0，0，0)， $w_Ψ$ V(0，0，0)和 $w_Ψ$ D(0，0，0)。这些输出按前单尺度变换中使用的相同的顺序串联成列(虽然这里是lx1矩阵)，并取代它们的近似系数。然后更新记账矩阵S2，以反映C1中的单个2X2逼近矩阵已被41x1详细信息和c2中的逼近矩阵所取代。因此，S2(end，：)再次表示原始图像的大小，S2(3，：)是三个细节系数矩阵在尺度1处的大小，S2(2，：)是标度为0的三个细节系数矩阵的大小，S2(1，：)是最终近似的大小。

2.2 不使用小波工具箱的FWT

这一小节，我们将去完成一对自定义函数——wavefilter和wavefast，从而代替前面章节的小波工具箱wfilters和wavedec2。我们的目的是为了计算快速小波变换的机制提供额外的理解，同时开始为基于小波的图像处理建立不用工具箱的“独立程序包”。

function [varargout] = wavefilter(wname, type)
% Check the input and output arguments.
error(nargchk(1, 2, nargin));

if (nargin == 1 && nargout ~= 4) || (nargin == 2 && nargout ~= 2)
   error('Invalid number of output arguments.'); 
end

if nargin == 1 && ~ischar(wname)
   error('WNAME must be a string.'); 
end

if nargin == 2 && ~ischar(type)
   error('TYPE must be a string.'); 
end
  
% Create filters for the requested wavelet.
switch lower(wname)
case {'haar', 'db1'}
   ld = [1 1]/sqrt(2);     hd = [-1 1]/sqrt(2);
   lr = ld;                hr = -hd;
   
case 'db4'
   ld = [-1.059740178499728e-002 3.288301166698295e-002 ...
         3.084138183598697e-002 -1.870348117188811e-001 ...
         -2.798376941698385e-002 6.308807679295904e-001 ...
         7.148465705525415e-001 2.303778133088552e-001];
   t = (0:7);
   hd = ld;    hd(end:-1:1) = cos(pi * t) .* ld;
   lr = ld;    lr(end:-1:1) = ld;
   hr = cos(pi * t) .* ld;
   
case 'sym4'
   ld = [-7.576571478927333e-002 -2.963552764599851e-002 ...
         4.976186676320155e-001 8.037387518059161e-001 ...
         2.978577956052774e-001 -9.921954357684722e-002 ...
         -1.260396726203783e-002 3.222310060404270e-002];
   t = (0:7);
   hd = ld;    hd(end:-1:1) = cos(pi * t) .* ld;
   lr = ld;    lr(end:-1:1) = ld;
   hr = cos(pi * t) .* ld;
   
case 'bior6.8'
   ld = [0 1.908831736481291e-003 -1.914286129088767e-003 ...
         -1.699063986760234e-002 1.193456527972926e-002 ...
         4.973290349094079e-002 -7.726317316720414e-002 ...
         -9.405920349573646e-002 4.207962846098268e-001 ...
         8.259229974584023e-001 4.207962846098268e-001 ...
         -9.405920349573646e-002 -7.726317316720414e-002 ...
         4.973290349094079e-002 1.193456527972926e-002 ...
         -1.699063986760234e-002 -1.914286129088767e-003 ...
         1.908831736481291e-003];
   hd = [0 0 0 1.442628250562444e-002 -1.446750489679015e-002 ...
         -7.872200106262882e-002 4.036797903033992e-002 ...
         4.178491091502746e-001 -7.589077294536542e-001 ...
         4.178491091502746e-001 4.036797903033992e-002 ...
         -7.872200106262882e-002 -1.446750489679015e-002 ...
         1.442628250562444e-002 0 0 0 0];
   t = (0:17);
   lr = cos(pi * (t + 1)) .* hd;
   hr = cos(pi * t) .* ld;
   
case 'jpeg9.7'
   ld = [0 0.02674875741080976 -0.01686411844287495 ...
         -0.07822326652898785 0.2668641184428723 ...
         0.6029490182363579 0.2668641184428723 ...
         -0.07822326652898785 -0.01686411844287495 ...
         0.02674875741080976];
   hd = [0 -0.09127176311424948 0.05754352622849957 ...
         0.5912717631142470 -1.115087052456994 ...
         0.5912717631142470 0.05754352622849957 ...
         -0.09127176311424948 0 0];
   t = (0:9);
   lr = cos(pi * (t + 1)) .* hd;
   hr = cos(pi * t) .* ld;
   
otherwise
   error('Unrecognizable wavelet name (WNAME).');
end

% Output the requested filters.
if (nargin == 1)
   varargout(1:4) = {ld, hd, lr, hr};
else
   switch lower(type(1))
   case 'd'
      varargout = {ld, hd};
   case 'r'
      varargout = {lr, hr};
   otherwise
      error('Unrecognizable filter TYPE.');
   end
end

function [c, s] = wavefast(x, n, varargin) 
error(nargchk(3, 4, nargin)); 
 
if nargin == 3 
   if ischar(varargin{1})    
      [lp, hp] = wavefilter(varargin{1}, 'd'); 
   else  
      error('Missing wavelet name.');    
   end 
else 
   lp = varargin{1};   hp = varargin{2};    
end 

% Get the filter length, 'lp', input array size, 'sx', and number of
% pages, 'pages', in extended 2-D array x. 
fl = length(lp);       sx = size(x);        pages = size(x, 3); 

if ((ndims(x) ~= 2) && (ndims(x) ~= 3)) || (min(sx) < 2) ...
        || ~isreal(x) || ~isnumeric(x) 
   error('X must be a real, numeric 2-D or 3-D matrix.');      
end 
   
if (ndims(lp) ~= 2) || ~isreal(lp) || ~isnumeric(lp) ... 
       || (ndims(hp) ~= 2) || ~isreal(hp) || ~isnumeric(hp) ... 
       || (fl ~= length(hp)) || rem(fl, 2) ~= 0 
   error(['LP and HP must be even and equal length real, ' ... 
          'numeric filter vectors.']);  
end 
   
if ~isreal(n) || ~isnumeric(n) || (n < 1) || (n > log2(max(sx))) 
   error(['N must be a real scalar between 1 and ' ... 
          'log2(max(size((X))).']);     
end 
   
% Init the starting output data structures and initial approximation. 
c = [];        s = sx(1:2);
app = cell(pages, 1);
for i = 1:pages
   app{i} = double(x(:, :, i));
end

% For each decomposition ... 
for i = 1:n 
   % Extend the approximation symmetrically. 
   [app, keep] = symextend(app, fl, pages); 
    
   % Convolve rows with HP and downsample. Then convolve columns 
   % with HP and LP to get the diagonal and vertical coefficients. 
   rows = symconv(app, hp, 'row', fl, keep, pages); 
   coefs = symconv(rows, hp, 'col', fl, keep, pages);
   c = addcoefs(c, coefs, pages);
   s = [size(coefs{1}); s];
   coefs = symconv(rows, lp, 'col', fl, keep, pages); 
   c = addcoefs(c, coefs, pages);
    
   % Convolve rows with LP and downsample. Then convolve columns 
   % with HP and LP to get the horizontal and next approximation 
   % coeffcients. 
   rows = symconv(app, lp, 'row', fl, keep, pages); 
   coefs = symconv(rows, hp, 'col', fl, keep, pages); 
   c = addcoefs(c, coefs, pages);
   app = symconv(rows, lp, 'col', fl, keep, pages);
end 
 
% Append the final approximation structures. 
c = addcoefs(c, app, pages); 
s = [size(app{1}); s];
if ndims(x) > 2
   s(:, 3) = size(x, 3);
end
 
%-------------------------------------------------------------------% 
function nc = addcoefs(c, x, pages) 
% Add 'pages' array coefficients to the wavelet decomposition vector. 

nc = c;
for i = pages:-1:1
   nc = [x{i}(:)' nc]; 
end
 
%-------------------------------------------------------------------% 
function [y, keep] = symextend(x, fl, pages) 
% Compute the number of coefficients to keep after convolution and 
% downsampling. Then extend the 'pages' arrays of x in both
% dimensions. 
 
y = cell(pages, 1);
for i = 1:pages
   keep = floor((fl + size(x{i}) - 1) / 2); 
   y{i} = padarray(x{i}, [(fl - 1) (fl - 1)], 'symmetric', 'both'); 
end
 
%-------------------------------------------------------------------% 
function y = symconv(x, h, type, fl, keep, pages) 
% For the 'pages' 2-D arrays in x, convolve the rows or columns with
% h, downsample, and extract the center section since symmetrically 
% extended. 
 
y = cell(pages, 1);
for i = 1:pages
   if strcmp(type, 'row') 
       y{i} = conv2(x{i}, h); 
       y{i} = y{i}(:, 1:2:end); 
       y{i} = y{i}(:, fl / 2 + 1:fl / 2 + keep(2)); 
   else 
       y{i} = conv2(x{i}, h'); 
       y{i} = y{i}(1:2:end, :); 
       y{i} = y{i}(fl / 2 + 1:fl / 2 + keep(1), :); 
   end 
end

3 小波分解结构的处理

前两部分的小波变换函数生成形式{c，S}的不可显示的数据结构，其中c是变换系数向量，Sis是定义c中系数排列的记账矩阵，处理图像必须能够检查和/或修改c。在本节中，我们正式定义了{c，S}，检查了一些小波工具箱函数来操作它，并开发了一组不用小波工具箱可以使用的自定义函数。然后使用这些函数建立一个通用的c显示例程。

3.1 使用变换分解向量c的小波工具箱函数

>> f = magic(8);
>> [c1, s1] = wavedec2(f, 3, 'haar');
>> size(c1)

ans =

     1    64

>> s1

s1 =

     1     1
     1     1
     2     2
     4     4
     8     8
>> approx = appcoef2(c1,s1,'haar')

approx =

  260.0000

>> horizdet2 = detcoef2( 'h', c1 , s1, 2)

horizdet2 =

   1.0e-13 *

         0   -0.2842
         0         0

>> newc1 = wthcoef2('h', c1 , s1, 2); 
>> newhorizdet2 = detcoef2('h', newc1 , s1 , 2)

newhorizdet2 =

     0     0
     0     0

这里，K是1，在单个8×8幻方图上用wavedec2对Haar小波进行三级分解。计算系数向量c_1，大小为1X64。由于s1是5x2，我们知道c1span(N-2)=(5-2)=3个分解层的系数。因此。它描述了填充3N+1=3(3)+1=10近似和细节系数子矩阵所需的元素。基于S1，这些子矩阵包括(A)分解级3的一个1X1逼近矩阵和3个1X1详细矩阵[见s1(1，：)和s1(2，：)]，(B)第2级的三个2X2详细矩阵[见S1(3，：)]，以及（c）第1级的三个4X4详细矩阵[见s1(4，：))。s1的第五行包含原始图像f的大小。

3.2 不使用小波工具箱编辑小波分解系数

function [nc, y] = wavecut(type, c, s, n)
error(nargchk(3, 4, nargin));
if nargin == 4   
   [nc, y] = wavework('cut', type, c, s, n);
else  
   [nc, y] = wavework('cut', type, c, s);  
end

function y = wavecopy(type, c, s, n)
error(nargchk(3, 4, nargin));
if nargin == 4   
   y = wavework('copy', type, c, s, n);
else  
   y = wavework('copy', type, c, s);  
end

function nc = wavepaste(type, c, s, n, x)
error(nargchk(5, 5, nargin))
nc = wavework('paste', type, c, s, n, x);

这里我们用自定义函数wavecut和wavecopy处理c

>> f = magic(8);
>> [c1, s1] = wavedec2(f, 3, 'haar');
>> approx = wavecopy('a', c1, s1)
approx =

  260.0000
>> horizdet2 = wavecopy('h', c1, s1, 2)
horizdet2 =

   1.0e-13 *

         0   -0.2842
         0         0

>> [newc1,horizdet2] = wavecut('h', c1 , s1, 2);
>> newhorizdet2 = wavecopy('h', newc1 , s1 , 2) 
newhorizdet2 =

     0     0
     0     0

这里提取的所有矩阵都与之前的例子一样。

3.3 用wavedispl函数显示变换系数

>> f = rgb2gray(imread('raccoon.jpg'));
>> imshow(f)
>> [c, s] = wavefast(f, 2, 'db4');
>> wavedisplay(c, s); title('(a) Automatic scaling; ');
>> figure; wavedisplay(c, s, 8);title('(b) additional scaling by 8; ');
>> figure; wavedisplay(c, s,-8) ; title('(c) absolute values scaled by 8. ');

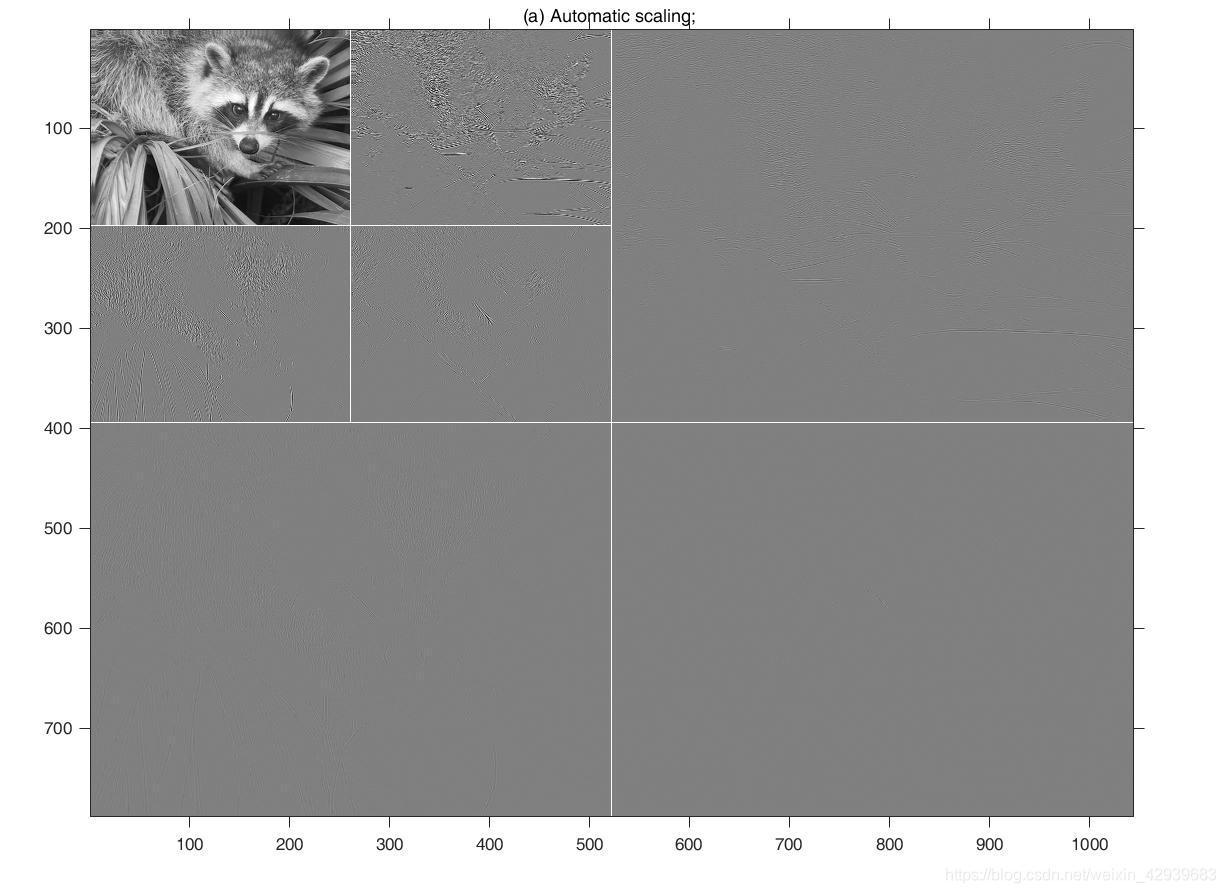
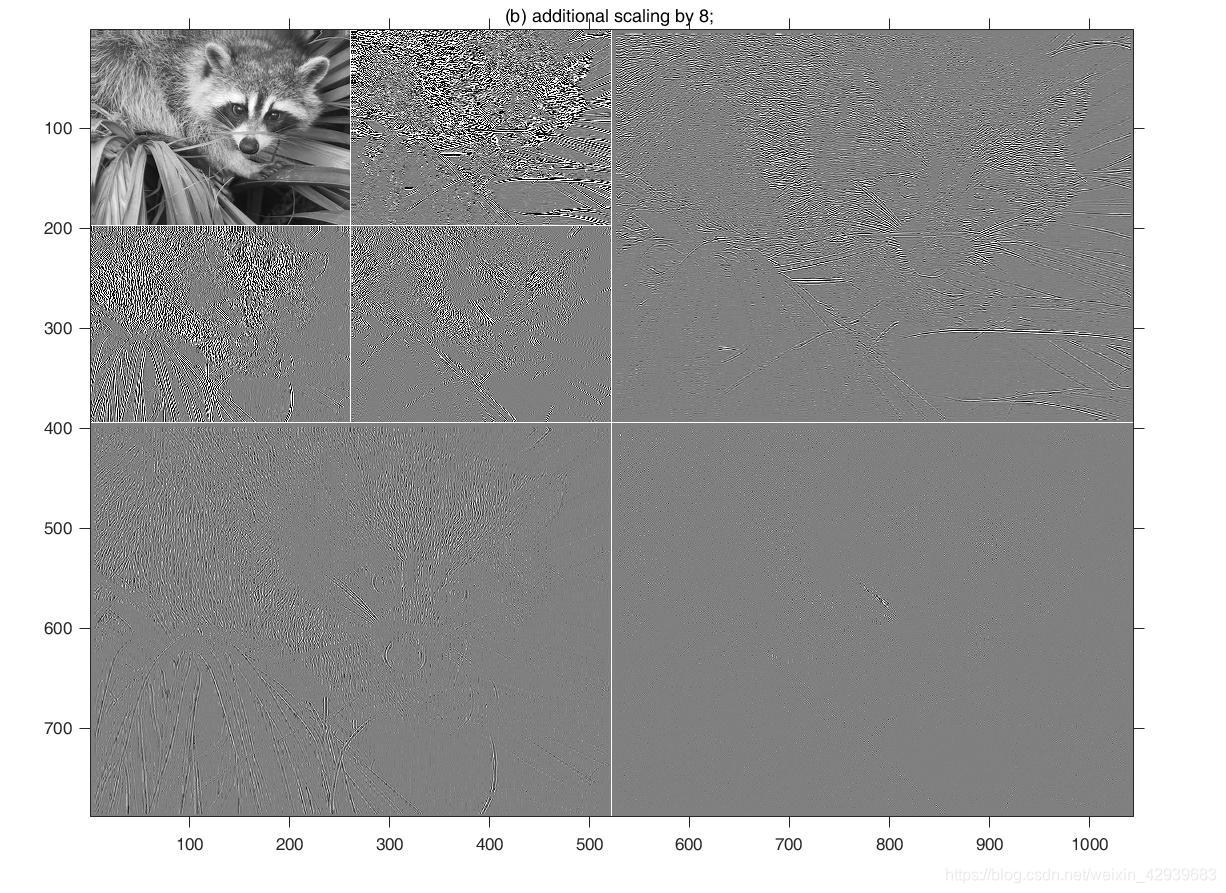
在这里插入图片描述

最后三个命令行生成的图像分别在(A)至©中显示。如果没有额外的缩放，(A)中的细节系数差异几乎是不可见的。在(B)中，通过将系数乘以8来增强这些差异。注意沿着级别1的系数子图像边界的中等灰度填充，插入是为了调节变换系数子图像的维数变化。（C）显示了取细节绝对值的效果。这里所有的填充为黑色。

4 图像中的小波

与在傅里叶域中一样，基于小波的图像处理的基本过程是：
（1）计算一幅图像的二维小波变换。
（2）修改变换系数。
（3）计算反变换

4.1 小波的定向性和边缘检测

>> f = rgb2gray(imread('jimei2.jpg'));
>> subplot(2, 2, 1);imshow(f); title('(a) A simple test image;');
>> [c, s] = wavefast(f, 1, 'sym4');
>> subplot(2, 2, 2); imshow(wavedisplay(c, s, -6)) ; title('(b) Its wavelet transform;');
>> [nc, y] = wavecut ('a', c, s) ; 
>> subplot(2, 2, 3); imshow(wavedisplay(nc, s, -6)) ; title('(c) the transform modified by zeroing all approximation coefficients;');
>> edges = abs (waveback (nc, s, 'sym4')) ;
>> subplot(2, 2, 4); imshow(mat2gray(edges)); title('( d) the edge image resulting from computing the absolute value of the inverse transform.');

在这里插入图片描述
图A中单尺度小波变换的水平、垂直及对角线的方向性在图B中可清楚地看到。例如，原始图像的水平边缘出现在图B中右上象限的水平细节系数中。图像的垂直边缘可以类似地在左下象限的垂直细节系数中看到，把这些信息合并成单一边缘图像。可把变换产生的近似系数简单地设为0，并计算反变换，再取绝对值。修改过的变换和得到的边缘图像分别显示在图C和图D中。

4.2 基于小波的图像平滑及模糊

>> f = rgb2gray(imread('raccoon.jpg'));
>> subplot(2,3,1),imshow(f),title('(a)the original image');
>> [c, s] = wavefast(f, 4, 'sym4');
>> subplot(2,3,2),wavedisplay(c, s, 20);title('(b)sym4 four wavelet transform results');
>> [c,g8] = wavezero(c, s,1,'sym4');title('(c)Set the details of scale 1 to 0 after the inverse transformation');
>> [c, g8] = wavezero(c, s, 2, 'sym4'); 
title('(d)Set the details of scale 2 to 0 after the inverse transformation');
>> [c, g8] = wavezero(c, s, 3, 'sym4');
title('(e)Set the details of scale 3 to 0 after the inverse transformation');
>> [c, g8] = wavezero(c, s, 4, 'sym4'); 
title('(f)Set the details of scale 4 to 0 after the inverse transformation');

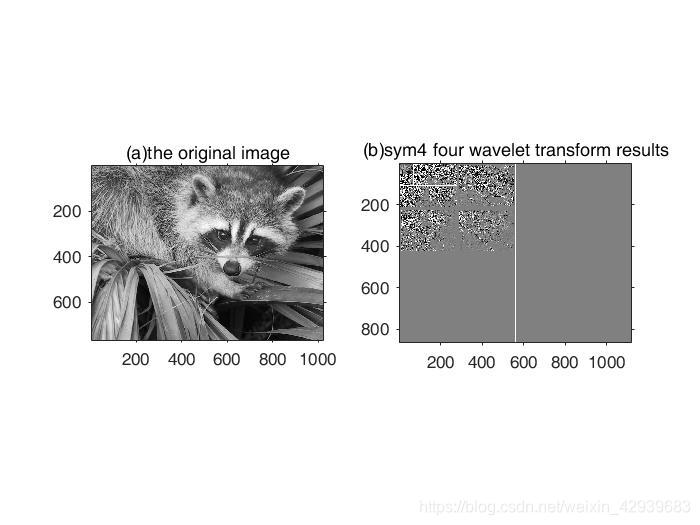
在这里插入图片描述

注意，图C中平滑后的图像只是稍微有些模糊，这源于这幅图像是通过将原始图像的小波变换的第一级细节系数设为零得到的。进一步的模糊效果如图D所示，往后不断将细节系数置为零，图像变得越来越模糊，这证明小波域里的尺度和傅里叶域里的频率紧密关联。

4.3 渐进重构

在浏览远程图像数据库以寻找特定图像，数据库中的每幅图像被存储为多尺度的小波分解，使用我们前几小节说过的通用格式，这个结构非常适合渐进重构应用。

f = rgb2gray(imread('raccoon.jpg'));
figure;[c, s] = wavefast(f, 4, 'jpeg9.7');
wavedisplay(c,s,8); 
title('(a)4 scaling wavelet decomposition coefficient (reconstruction)');
f=wavecopy('a',c,s);
figure,imshow(mat2gray(f));
title('(b)Wavelet image of myopia coefficient');
[c s]=waveback(c,s,'jpeg9.7',1);
f=wavecopy('a',c,s);
figure,imshow(mat2gray(f));
title('(c)The image was reconstructed 1 time');
[c s]=waveback(c,s,'jpeg9.7',1);
f=wavecopy('a',c,s);
figure,imshow(mat2gray(f));
title('(d)The image was reconstructed twice');
[c s]=waveback(c,s,'jpeg9.7',1);
f=wavecopy('a',c,s);
figure,imshow(mat2gray(f))
title('(e)The image was reconstructed 3 times');
[c s]=waveback(c,s,'jpeg9.7',1);
f=wavecopy('a',c,s);
figure,imshow(mat2gray(f));
title('(f)The image was reconstructed 4 times');