利用AdaBoost元算法提高分类性能
定义
- 集成方法(ensemble method) 或元算法(meta-algorithm):我们可以将不同分类器组合起来,这种组合的结果则被称为集成方法(ensemble method) 或元算法(meta-algorithm)
- 集成会有多种形式:可以是不同算法的集成,也可以是同一算法在不同设置下的集成,还可以是数据集不同部分分配给不同分类器之后的集成。
- 自举汇聚法(boostrap aggregating),也称bagging方法,基于数据随机重抽样的分类器构建方法,
- boosting:不论是在boosting还是bagging当中,所使用的多个分类器的类型都是一致的。但是在前者当中,不同的分类器是通过串行训练而获得的,每个新分类器都根据已训练出的分类器的性能来进行训练。boosting是通过集中关注被已有分类器错分的那些数据来获得新的分类器。由于boosting分类的结果是基于所有分类器的加权求和结果的,因此boosting与bagging不太一样。bagging中的分类器权重是相等的,而boosting中的分类器权重并不相等,每个权重代表的是其对应分类器在上一轮迭代中的成功度。boosting其中一个最流行的版本是AdaBoost。
- 弱分类器:“弱”意味着分类器的性能比随机猜测要略好,但是也不会好太多,也就是说弱分类器的正确率会高于50%,
AdaBoost 训练算法
- AdaBoost 是adaptive boosting (自适应boosting)的缩写
- 其运行过程如下:
- 对训练集中的每一个样本初始化一个权重(一般初始化为相等权值),构成向量D
- 在训练数据集上训练出一个弱分类器,并计算这个分类器的错误率 ϵ \epsilon ϵ=未正确分类的样本数目与样本总数目的比值
- 计算当前分类器的权重 α = 1 2 l n ( 1 − ϵ ϵ ) \alpha=\frac{1}{2}ln(\frac{1-\epsilon}{\epsilon}) α=21ln(ϵ1−ϵ)
- 在同一数据集上再次训练,更新每个样本的权重,其中上一次分类正确的样本权重会降低,分类错误的样本权重会提高。D的计算方法如下:
- D是一个概率分布向量,所有元素之和为1.0,一开始所有元素都会初始化为1/m
- 正确分类的样本: D i ( t + 1 ) = D i ( t ) e − α S u m ( D ) D_i^{(t+1)}=\frac{D_i^{(t)}e^{-\alpha}}{Sum(D)} Di(t+1)=Sum(D)Di(t)e−α
- e − α = e − 1 2 l n ( 1 − ϵ ϵ ) = ϵ 1 − ϵ e^{-\alpha}=e^{-\frac{1}{2}ln(\frac{1-\epsilon}{\epsilon})}=\sqrt{\frac{\epsilon}{1-\epsilon}} e−α=e−21ln(ϵ1−ϵ)=1−ϵϵ
- 错误分类的样本: D i ( t + 1 ) = D i ( t ) e α S u m ( D ) D_i^{(t+1)}=\frac{D_i^{(t)}e^{\alpha}}{Sum(D)} Di(t+1)=Sum(D)Di(t)eα
- e − α = e − 1 2 l n ( 1 − ϵ ϵ ) = 1 − ϵ ϵ e^{-\alpha}=e^{-\frac{1}{2}ln(\frac{1-\epsilon}{\epsilon})}=\sqrt{\frac{1-\epsilon}{\epsilon}} e−α=e−21ln(ϵ1−ϵ)=ϵ1−ϵ
- 重复训练和调整权重,直到训练错误率为0或弱分类器数目达到要求
基于单层决策树构建弱分类器
- 单层决策树也称决策树桩(decision stump)是一种简单的决策树,它仅基于单个特征来做决策。
- 通过遍历数据集的特征和单层决策树的某些参数找到具有最低错误率的单层决策树
- 单层决策树的参数有:
- 与数据比较的阈值
- 和阈值比较时是用大于,还是小于
- 因而构建这个单层决策树需要三层循环
- 对数据集中的每一个特征
- 对每个步长(阈值),阈值按设定的步长增加
- 对每个不等号(大于,小于):建立单层决策树并利用加权数据集对它进行测试,如果错误率低于minError,则将当前决策树设为最佳单层决策树。
- 返回最佳单层决策树
- 单层决策树生成函数
from numpy import *
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps #阈值增加的步长
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0 #预测正确将误差置为0
weightedError = D.T*errArr #calc total error multiplied by D 计算所有样本的预测误差
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i # 单层决策树对应的特征
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst #bestStump存储最佳单层决策树的信息
训练算法:完整Adaboost训练算法的实现
- 基于单层决策树的AdaBoost训练过程
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) # D是一个概率分布向量,所有元素之和为1.0 init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
#迭代次数40次
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
#print "D:",D.T
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
# max(error,1e-16) 确保没有错误时不会发生除0溢出
# 当前分类器的权重alpha 是一个数字
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
#print "classEst: ",classEst.T
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #分类正确时alpha为负,错误时alpha为正,classLabels的元素是-1,1 exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst #列向量aggClassEst,记录每个数据点的类别估计累计值
#print "aggClassEst: ",aggClassEst.T
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1))) # 估计累计值与标签的符号相同则认为估计正确,得到的值为0
errorRate = aggErrors.sum()/m
print "total error: ",errorRate
if errorRate == 0.0: break
return weakClassArr,aggClassEst
测试算法:基于 AdaBoost 的分类
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print aggClassEst
return sign(aggClassEst)
- 函数的参数:
- datToClass 带预测的数据
- classifierArr 利用训练出的多个弱分类器组成的数组
优缺点
优点:
- 具有很高的精度
- 相对于bagging算法和Random Forest算法,AdaBoost充分考虑的每个分类器的权重。
- 可以使用各种方法构建子分类器,Adaboost算法提供的是框架
- 简单,不用做特征筛选
缺点:
- 训练时间长
- 执行效果依赖于弱分类器的选择
- 数据不平衡导致分类精度下降。
非均衡分类问题
- 正确率precision :预测为正例的样本中真正的正例所占的比例 = TP/(TP+FP)
- 召回率recall:预测对的真实正例占所有真实正例的比例 = TP/(TP+FN)
- 精确率accuracy:预测对的样本占所有样本的比例 = (TP+TF)/(TP+FP+TN+FN)
- F1=2PR/(P+R) -> 1/F1=1/2 * (1/P + 1/R)
- ROC曲线 y轴为真阳率,x轴为假阳率
- 真阳率 TPR :在所有实际为阳性的样本中,正确地预测为阳性样本所占的比例 TP/(TP+FN) (即召回率)
- 假阳率 FPR:在所有实际为阴性的样本中,被错误判断为阳性样本所占的比例 FP/(TN+FP)
假设如下就是某个医生的诊断统计图,直线代表阈值。我们遍历所有的阈值,能够在ROC平面上得到如下的ROC曲线。
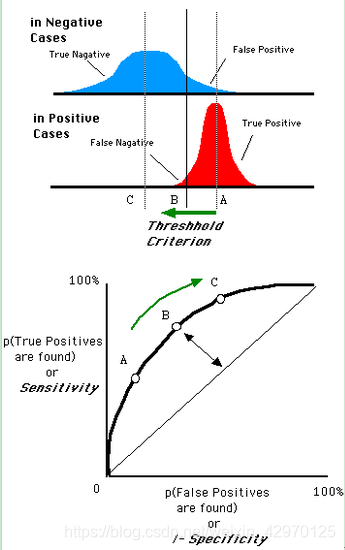
- AUC area under the curve值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
- AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
ROC曲线的绘制及AUC计算函数
- 为了画出ROC曲线,分类器必须提供每个样例被判为阳性或者阴性的可信程度值,可以用于衡量给定分类器的预测强度。
- 因为需要遍历所有的阈值,首先要将分类样例按照其预测强度从小到大排序,将每个预测强度作为阈值。
- y轴是真阳率,y轴的步长应该是 1/正例的个数
- x轴是假阳率,x轴的步长应该是 1/负例的个数
- 假如测试样例中有10个正例,5个负例,初始条件下,阈值无限小,真阳率和假阳率都为 1 (觉得抽象请参照上图)
- 遍历每个阈值时,遇到正例则 原真阳率 - 一个步长 = 当前真阳率 (假如遇到n个正例,真阳率=1-n/10)
- 这是因为预测强度从无限小到当前阈值,你的预测都是负,此时出现正例,有正例没有被正确预测所以真阳率下降
- 同理,遍历阈值时,遇到负例 当前假阳率=原假阳率 - 一个步长,有负例被正确预测了所以假阳率下降
- 计算AUC,我们需要对多个小矩形的面积进行累加。这些小矩形的宽度是xStep,因此可以先对所有矩形的高度进行累加,最后再乘以xStep得到其总面积。
def plotROC(predStrengths, classLabels):
'''
predStrengths:一个行向量组成的矩阵,是分类器和训练函数在应用到sign()函数之前产生对每个测试样本的预测强度(即aggClassEst )
classLabels:测试样本的标签
'''
import matplotlib.pyplot as plt
cur = (1.0,1.0) #cursor
ySum = 0.0 #variable to calculate AUC
numPosClas = sum(array(classLabels)==1.0)
yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
#loop through all the values, drawing a line segment at each point
for index in sortedIndicies.tolist()[0]:
if classLabels[index] == 1.0:
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0;
ySum += cur[1]
#draw line from cur to (cur[0]-delX,cur[1]-delY)
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
cur = (cur[0]-delX,cur[1]-delY)
ax.plot([0,1],[0,1],'b--')
plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
plt.title('ROC curve for AdaBoost horse colic detection system')
ax.axis([0,1,0,1])
plt.show()
print "the Area Under the Curve is: ",ySum*xStep
基于代价函数的分类器决策控制
- 处理调节分类器的阈值外,还有其他可以处理非均衡分类代价的方法,其中一种称为 代价敏感的学习 cost-sensitive learning
- 我们可以基于代价矩阵计算总代价,如:TP*(-5)+FN1+FP50+TN*0
- 两种分类错误的代价是不一样的,两种分类正确的收益也是不一样的,在构造分类器时,就可以选择代价最小的分类器了
- 在AdaBoost中,可以基于代价函数来调整错误权重向量D。
- 在朴素贝叶斯中,可以选择具有最小期望代价而不是最大概率的类别作为最后的结果。
处理非均衡问题的数据抽样方法
- 另外一种针对非均衡问题调节分类器的方法,可以通过欠抽样 undersampling 或 过抽样 oversampling 来实现对分类器的训练数据改造。
扩展:提升树
- 提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法,以决策树为基函数的提升方法称为提升树(boosting tree)
- 对分类问题决策树是二叉分类树,对回归问题是二叉回归树
- 对于二分类问题,提升树算法只需将基本分类器限制为二类分类树即可,
提升树算法是Adaboost算法的特殊情况。 - 由于树的新型组合可以很好地拟合训练数据,即使数据中的输入与输出之间的关系和复杂也是如此,所以提升树是一个高功能的学习算法。
- 提升树学习算法可以针对不同问题:包括使用平方误差损失函数的回归问题,用指数损失函数的分类问题,以及用一般损失函数的一般决策问题。
- 指数损失函数: L ( y , f ( x ) ) = exp ( − y f ( x ) ) L(y,f(x))=\exp(-yf(x)) L(y,f(x))=exp(−yf(x))
- 前向分布算法: 前向分步算法将同时求解从m=1到M所有参数的优化问题简化为逐次求解各个参数的优化问题。例如对于Adaboost来说就是逐次求解分类器的权重。
- 回归问题的提升树算法
- 输入:训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},损失函数L(y,f(x));
- 输出:回归树 f ^ ( x ) \hat f(x) f^(x)
- 初始化 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0
- 对于 m = 1,2,…M (算法迭代的次数)
a. 计算残差 r m r = y i − f m − 1 ( x i ) r_{mr}=y_i-f_{m-1}(x_i) rmr=yi−fm−1(xi)
b. 拟合残差 r m r r_{mr} rmr学习一个回归树 T ( x ; θ m ) T(x;\theta_m) T(x;θm)
c. 更新 f m ( x ) = f m − 1 + T ( x ; θ m ) f_m(x)=f_{m-1}+T(x;\theta_m) fm(x)=fm−1+T(x;θm) - 得到回归问题提升树 f M ( x ) = ∑ m = 1 M T ( x ; θ m ) f_M(x)=\sum_{m=1}^{M}T(x;\theta_m) fM(x)=∑m=1MT(x;θm)
- 拟合当前模型的残差,找到使得损失函数最小的模型。
- 提升树利用加法模型和前向分步算法实现优化过程。当损失函数是平方损失和指数损失函数的时候,每一步优化是很简单的。但对一般损失函数而言,往往每一步优化并不那么容易。
- 针对这个问题,就提出梯度提升算法,利用最速下降的近似方法,其关键是利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值,拟合一个回归树。
- 梯度提升算法
- 输入:训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},损失函数L(y,f(x));
- 输出:回归树 f ^ ( x ) \hat f(x) f^(x)
- 初始化 f 0 ( x ) = a r g m i n ∑ i = 1 N L ( y i , c ) f_0(x)=arg min \sum_{i=1}^{N}L(y_i,c) f0(x)=argmin∑i=1NL(yi,c)
- 对于 m = 1,2,…M (算法迭代的次数)
a. 对于 i=1,2…,N (样本的个数) r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi}=-[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
b. 对 r m i r_{mi} rmi拟合一个回归树,得到第M棵树的叶结点区域 R m j R_{mj} Rmj,j=1,2,…,J ()
c. 对j=1,2,…,J ,计算
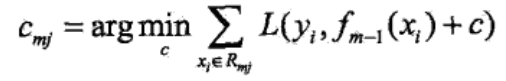
d. 更新 f m ( x ) = f m − 1 ( x ) + ∑ j = 1 j c m j I ( x ∈ R m j ) f_m(x)=f_{m-1}(x)+\sum_{j=1}^{j}c_{mj}I(x \in R_{mj}) fm(x)=fm−1(x)+∑j=1jcmjI(x∈Rmj) - 得到回归树 f ^ ( x ) = f M ( x ) = ∑ m = 1 M ∑ j = 1 J c m j I ( x ∈ R m j ) \hat f(x)=f_M(x)=\sum_{m=1}^{M}\sum_{j=1}^{J}c_{mj}I(x \in R_{mj}) f^(x)=fM(x)=m=1∑Mj=1∑JcmjI(x∈Rmj)





















 3361
3361











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








