在多目标优化中,分析两个目标是否存在权衡关系通常包括以下步骤:
-
数据收集:收集多目标优化的结果数据,这些数据包含了不同决策变量配置下的目标函数值。
-
数据可视化:使用散点图或其他可视化工具来展示不同决策方案下两个目标的值。这种图通常被称为Pareto前沿图或权衡曲线。
-
Pareto前沿分析:
- 在理想情况下,如果两个目标没有权衡关系,那么改进一个目标的值不会恶化另一个目标的值。在Pareto前沿图中,这意味着所有最优点将会集中在某个角落。
- 如果存在权衡,那么一般会观察到一条边界,表示当一个目标的值提高时,另一个目标的值会降低。这个边界就是Pareto前沿。
-
相关性分析:
- 计算两个目标之间的相关系数(如皮尔逊相关系数),以量化它们之间的线性关系强度。
- 如果相关系数接近-1或1,表明两个目标之间有很强的负相关或正相关。负相关通常表明存在权衡。
这里我们使用相关系数矩阵分析它们之间的权衡关系
在统计学中,相关系数矩阵用于衡量两个或多个变量之间的线性关系的强度和方向。相关系数的值范围从-1到1:
- 接近1的值表明存在强正相关:一个变量的增加伴随着另一个变量的增加。
- 接近-1的值表明存在强负相关:一个变量的增加伴随着另一个变量的减少。
- 接近0的值表明两个变量之间没有线性相关或者相关性非常弱。
相关系数矩阵是一个方阵,每个元素(i, j)代表变量i和变量j之间的相关系数。对于任何变量,其与自身的相关系数总是1,因为任何变量与自身总是完全正相关的。因此,相关系数矩阵的对角线【对角线是指从左上角到右下角的线】总是1。
这里是如何分析相关系数矩阵【其实也就是分析“反对角线”的值,看它与-1,0,1之间的关系】:
-
查看对角线以外的值:矩阵的对角线将始终是1,因为它表示变量与自身的相关性。对角线以外的值表示不同变量之间的相关性。
-
分析变量对之间的相关性:选择两个变量,找到它们在相关系数矩阵中对应的元素,这个数值告诉你它们之间的相关性如何。
例如,如果你有两个目标函数值Objective1和Objective2,相关系数矩阵可能如下所示:
Objective1 Objective2
Objective1 1.000000 -0.970725
Objective2 -0.970725 1.000000这个结果表示Objective1和Objective2之间有很强的负相关(接近-1),暗示了在这两个目标之间存在潜在的权衡关系。在多目标优化中,如果你试图同时最大化或最小化这两个目标,这通常意味着改善其中一个目标会牺牲另一个目标的表现。
一个简单的分析代码
import matplotlib.pyplot as plt
import pandas as pd
# 假设你有一个DataFrame,其中包含两个目标的值
df = pd.DataFrame({
'Objective1': [0.1, 0.2, 0.3, 0.4, 0.5],
'Objective2': [0.5, 0.4, 0.35, 0.25, 0.15]
})
# 绘制散点图来展示两个目标的权衡关系
plt.scatter(df['Objective1'], df['Objective2'])
plt.xlabel('Objective 1')
plt.ylabel('Objective 2')
plt.title('Trade-off Analysis between Two Objectives')
plt.show()
# 计算并打印相关系数
correlation = df.corr()
print("Correlation matrix:")
print(correlation)
对csv文件中每一行smiles的两个属性进行的权衡分析
import matplotlib.pyplot as plt
import pandas as pd
# 从CSV文件中读取数据
df = pd.read_csv('csv/test_PCA.csv')
# 确保列名与CSV文件中的列名匹配
# 这里我们假设列名为"qed"和"SA"
objective_1 = df['qed']
objective_2 = df['sa']
# 绘制散点图来展示两个目标的权衡关系
plt.scatter(objective_1, objective_2)
plt.xlabel('QED')
plt.ylabel('SA')
plt.title('Trade-off Analysis between QED and SA')
plt.show()
# 计算并打印相关系数矩阵
correlation = df[['qed', 'sa']].corr() # 只选择我们感兴趣的两列
print("Correlation matrix:")
print(correlation)
输出:
Correlation matrix:
qed sa
qed 1.000000 -0.242494
sa -0.242494 1.000000感觉还是存在一定的权衡关系的:
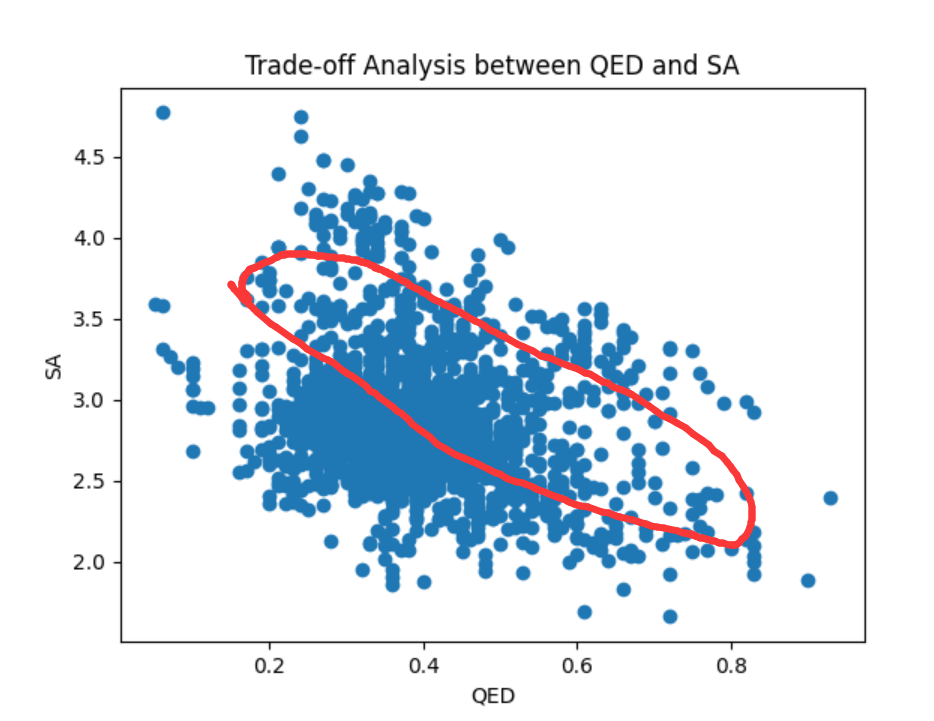








 本文介绍了在多目标优化中分析目标间权衡关系的方法,包括数据收集、Pareto前沿图的使用、相关系数的计算以及通过散点图和相关系数矩阵展示目标间的线性关系。实例展示了如何通过Python进行QED和SA的目标权衡分析。
本文介绍了在多目标优化中分析目标间权衡关系的方法,包括数据收集、Pareto前沿图的使用、相关系数的计算以及通过散点图和相关系数矩阵展示目标间的线性关系。实例展示了如何通过Python进行QED和SA的目标权衡分析。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










