逻辑回归是为了解决分类问题而出现的
假设函数
h
θ
(
x
)
=
g
(
θ
T
x
)
h_\theta(x)=g(\theta^Tx)
hθ(x)=g(θTx)
g
(
z
)
=
1
1
−
e
−
z
g(z)=\frac{1}{1-e^{-z}}
g(z)=1−e−z1
g ( z ) g(z) g(z)图像如下::
g ( z ) g(z) g(z)叫做sigmoid函数,目的是将z映射到0-1之间
当 g ( z ) ≥ 0.5 时 y = 1 g(z)\ge0.5时y=1 g(z)≥0.5时y=1,当$g(z)<0.5时y=1当 z ≥ 0 时 g ( z ) ≥ 0.5 z\ge0时g(z)\ge0.5 z≥0时g(z)≥0.5,当 z < 0 时 g ( z ) < 0.5 z<0时g(z)<0.5 z<0时g(z)<0.5
决策边界
假设我们的预测函数为:
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
)
h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)
hθ(x)=g(θ0+θ1x1+θ2x2)
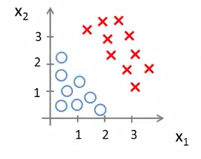
训练集如下:
由之前的结论可得:
当
y
=
1
时
,
θ
0
+
θ
1
x
1
+
θ
2
x
2
≥
0
当y=1时,\theta_0+\theta_1x_1+\theta_2x_2 \ge 0
当y=1时,θ0+θ1x1+θ2x2≥0
假设我们已经拟合参数:
θ
=
[
3
,
1
,
1
]
\theta = [3,1,1]
θ=[3,1,1]
所以只要有任何参数满足:
−
3
+
x
1
+
x
2
≥
0
-3+x_1+x_2\ge0
−3+x1+x2≥0
我们的假设函数就会认为
y
=
1
y=1
y=1
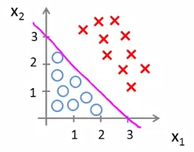
如果我们画出
x
1
+
x
2
=
3
x_1+x_2=3
x1+x2=3这条直线:
这条直线左边都会被预测为 y = 1 y=1 y=1,右边都会被预测为 y = 0 y=0 y=0
这条线就叫做决策边界
代价函数
线性回归的代价函数如下:
J
(
θ
)
=
1
m
∑
i
=
1
m
1
2
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta)=\frac1m\sum_{i=1}^m\frac12(h_\theta(x^{(i)})-y^{(i)})^2
J(θ)=m1i=1∑m21(hθ(x(i))−y(i))2
换一种形式:
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
=
1
2
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta)=\frac1m\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})\\ Cost(h_\theta(x^{(i)}),y^{(i)})=\frac12(h_\theta(x^{(i)})-y^{(i)})^2
J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))Cost(hθ(x(i)),y(i))=21(hθ(x(i))−y(i))2
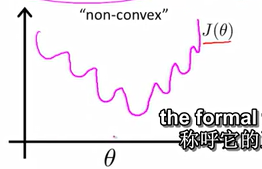
如果直接使用线性回归的代价函数,那么代价函数将会是个非凸函数(non-convex),将会有许多局部最优点,图像如下:
所以我们使用另一种代价函数:
l
o
g
(
z
)
log(z)
log(z)图像如下:
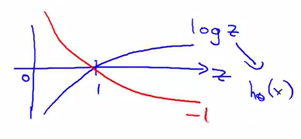
取
0
−
1
0-1
0−1:
如果 y = 1 y=1 y=1
这个函数有很好的特性,如果 y = 1 , h θ ( x ) = 1 , c o s t = 0 y=1,h_\theta(x)=1,cost=0 y=1,hθ(x)=1,cost=0
如果 y = 1 , h θ ( x ) → 0 , c o s t → ∞ y=1,h_\theta(x)\to0,cost\to\infty y=1,hθ(x)→0,cost→∞
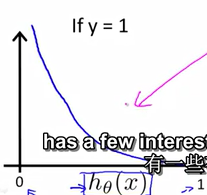
如果 y = 0 y=0 y=0
这个函数正好相反,如果 y = 0 , h θ ( x ) = 0 , c o s t = 0 y=0,h_\theta(x)=0,cost=0 y=0,hθ(x)=0,cost=0
如果 y = 0 , h θ ( x ) → 1 , , c o s t → ∞ y=0,h_\theta(x)\to1,,cost\to\infty y=0,hθ(x)→1,,cost→∞
为了简洁,把
合成一个函数:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
Cost(h_\theta(x),y)=-y \ log(h_\theta(x))-(1-y)log(1-h_\theta(x))
Cost(hθ(x),y)=−y log(hθ(x))−(1−y)log(1−hθ(x))
所以:
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
\begin{aligned} J(\theta)&=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})\\ &=-\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \end{aligned}
J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]









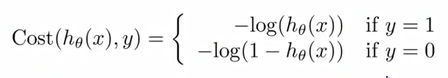
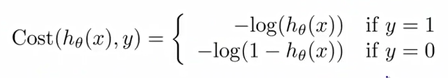














 1266
1266











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








