poj 1180 Batch Scheduling 斜率优化dp

题目:http://poj.org/problem?id=1180

对于这道题，可以写出一个一维dp方程

sumt ： t（每个任务所需要时间）的前缀和      

sumf ： f（每个人物的费用系数）的前缀和

dp[i]: 执行以第i个任务为结尾的时候总费用最小

那么其实不用管前面已经分了多少段，对于每一个小于i的j，都可以尝试以j~i为一段，

但是一段开始之前需要额外付出s的时间代价，这对以后都有影响，但是可以提前计算影响，并假如该次dp中

此时时间复杂度为O(N^2)

对于每一个dp[i]，可以将i看成常量提出来，以求找到化简方法

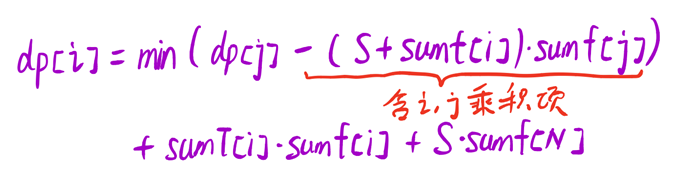
对于这种含ij乘积的，可以使用斜率优化dp ， 将dp[i]看成y ， sumf[j]看成x ，整体看成函数，此时min可以去掉

 

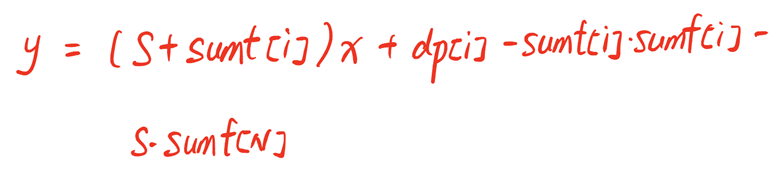
可以看出x，y分别是一个一个点，   要使得dp[i]最大，则线断截距最大，因为含i的部分看成常数，所以该直线斜率固定

j从小到大读入，所以sumf[j]是递增的，也就是x是递增的读入，考虑这种情况下什么时候截距最小

当AB 斜率小于k ， BC斜率大于k 的时候，B就是最优答案。

也就是B之前的直线斜率需要小于k，B之后的直线斜率需要大于k，因此可以使用优先队列维护所有连续的大于k的直线，取最左端则是答案。

注意到斜率的表达式，随着i的增大斜率必然是递增的。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#define ll long long 
#define ull unsigned long long 
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 1e4 + 7;
int sumt[maxn], sumf[maxn];
int dp[1000007], q[maxn];
int main() {
	int n, s;
	cin >> n >> s;
	for (int i = 1; i <= n; i++) {
		scanf("%d %d", sumt + i, sumf + i);
		sumt[i] += sumt[i - 1];
		sumf[i] += sumf[i - 1];
	}
	int l = 1, r = 1;
	dp[0] = 0;
	q[1] = 0;
	for (int i = 1; i <= n; i++) {
		while (l < r && (dp[q[l + 1]] - dp[q[l]])  <= (sumt[i] + s)*(sumf[q[l + 1]] - sumf[q[l]]))  //斜率除法变乘法
			l++;
		dp[i] = dp[q[l]] - (sumt[i] + s)*sumf[q[l]] + sumt[i] * sumf[i] + s * sumf[n];
		while (l < r && (dp[i] - dp[q[r]])*(sumf[q[r]] - sumf[q[r - 1]]) <= (dp[q[r]] - dp[q[r - 1]])*(sumf[i] - sumf[q[r]]))
			r--;
		q[++r] = i;
	}
	cout << dp[n] << endl;
	return 0;
}