前言
之前用标准遗传算法实现了函数寻找最大值的功能:
https://blog.csdn.net/weixin_43210097/article/details/119537408?spm=1001.2014.3001.5501
今天这篇代码依然是关于遗传算法优化的,但是加入了君主交叉的方式,同时是实数编码优化方式,与之前的二进制优化有不小的差别。
正文
优化目标是寻找一组X(一共10个),使得其平方和最小:
君主交叉:
每次选出表现最好的个体(君主),把它的染色体与整个种群中一半的个体交叉,增大君主染色体在整个种群中的比例。下方的代码仅仅是运用了君主交叉方式,除了君主交叉之外还包含了普通的交叉过程。
代码实现
import numpy as np
import matplotlib.pyplot as plt
# import math as mt
import seaborn as sns
sns.set_style('darkgrid')
def funcl(x):
y=0
for i in range(len(x)):
y=y+x[i]**2
return y
#%%
NP=100 #初始化种群数
D=10 #单条染色体基因数目10
Pc=0.8 #交叉率
Pm=0.1 #变异率
G=200 #最大遗传代数
Xs=20 #上限
Xx=-20 #下限
jiyi=np.random.rand(NP,D)
f=jiyi*(Xs-Xx)+Xx #随机获得初始种群
FIT=[]
sortf=[]
trace=[]
xtrace=[]
xtracemin=[]
test=[]
for i in range(NP):
FIT.append(funcl(f[i])) #适应度函数
sortFIT=np.sort(FIT) #升序排序
index= np.argsort(FIT) #升序对应索引
for i in range(len(f)):
sortf.append(f[index[i]]) #得到升序顺序对应的种群
#%%遗传算法循环
for i in range(G):
print(i)
Emper=sortf[0] #产生君主
nf=sortf #出新的种群,在其基础上进行交叉、变异
for M in range(0,NP,2):
p=np.random.rand() #君主交叉
if p<Pc:
for j in range(D):
nf[M][j]=Emper[j] #将君主的染色体给偶数索引的染色体,
# 我觉得这一步好像谈不上交叉,只是单纯地将君主染色体所占整体比重加大了
# 人为再加一手传统的交叉过程,到时候将这个过程删除,看看影响结果不
for M in range(0,NP,2):
p=np.random.rand() #交叉
if p<Pc:
q=np.random.randint(0,high=2,size=(1,D))[0].tolist()
for j in range(D):
if q[j]==1:
temp=nf[M+1][j]
nf[M+1][j]=nf[M][j]
nf[M][j]=temp
for M in range(NP): #变异
for n in range(D):
p=np.random.rand()
if p<Pm:
nf[M][n]=np.random.rand()*(Xs-Xx)+Xx
#交叉变异结束之后,新一代nf加上前代f共2*NP个个体进行筛选
newf=np.vstack((sortf,nf)) #垂直方向累加两个f
newFIT=[]
for j in range(len(newf)):
newFIT.append(funcl(newf[j])) #适应度函数
sortFIT=np.sort(newFIT) #升序排序
index= np.argsort(newFIT) #升序对应索引
maxfit=max(newFIT)
minfit=min(newFIT)
sortf=[]
for j in range(len(f)):
sortf.append(newf[index[j]]) #得到升序顺序对应的种群
trace.append(minfit)
st=sortf[0].tolist()
xtrace.append(st)
xvalue=[]
for i in range(len(xtrace)):
xvalue.append(xtrace[i][0])
plt.plot(trace,color='green', marker='o',linewidth=2, markersize=3)
plt.xlabel('Number of iterations',fontsize = 10)
plt.ylabel('minyvalue',fontsize = 10)
plt.savefig('pic4',bbox_inches = 'tight',pad_inches = 0,dpi =350)
plt.close()
plt.scatter(list(range(0,200)),xvalue,color='red',s=3) #s参数设置点的大小
plt.xlabel('Number of iterations',fontsize = 10)
plt.ylabel('x',fontsize = 10)
plt.savefig('pic5',bbox_inches = 'tight',pad_inches = 0,dpi =350)
plt.close()结果展示
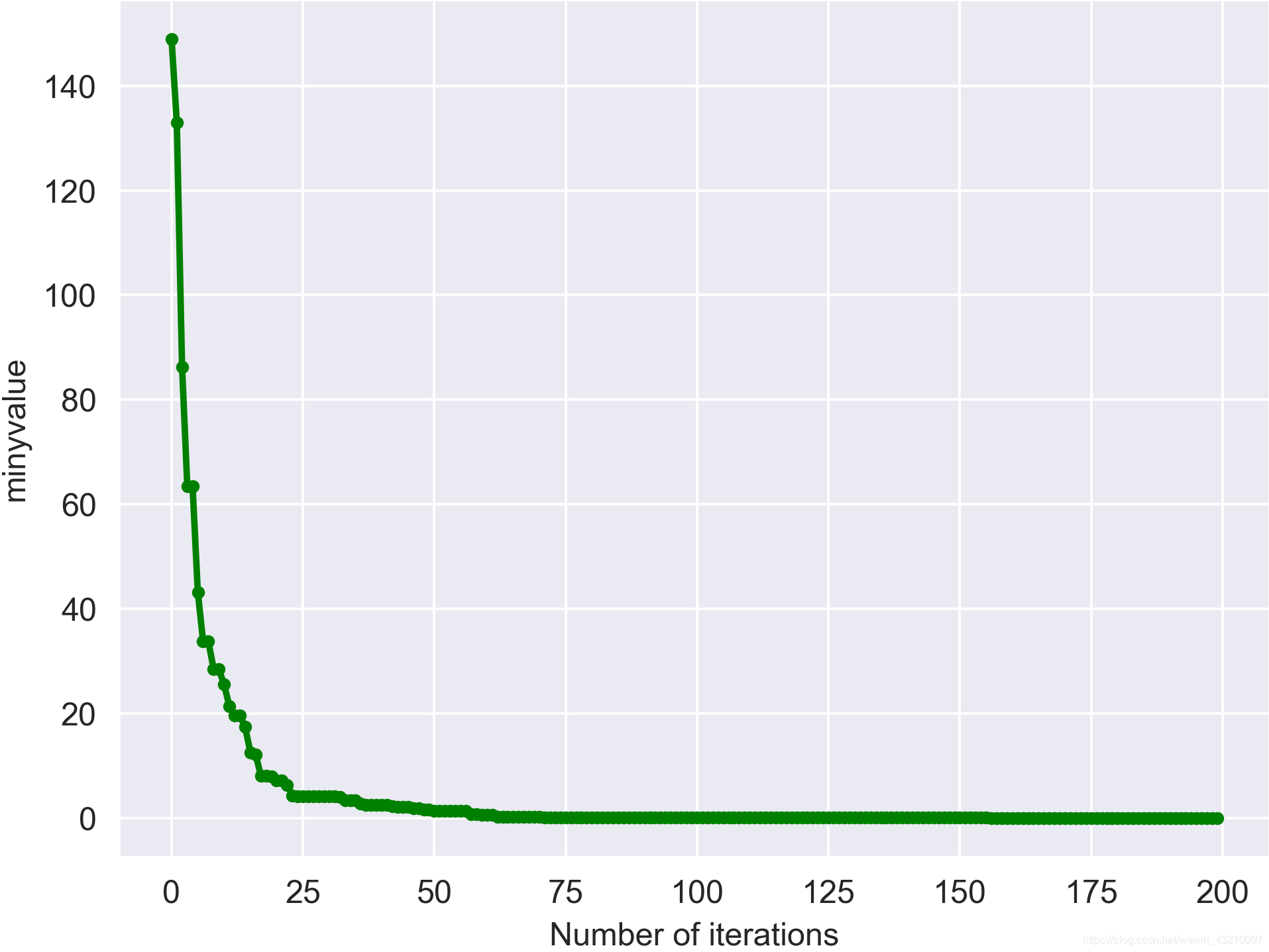
y的收敛曲线如下所示:收敛速度还是很快的。
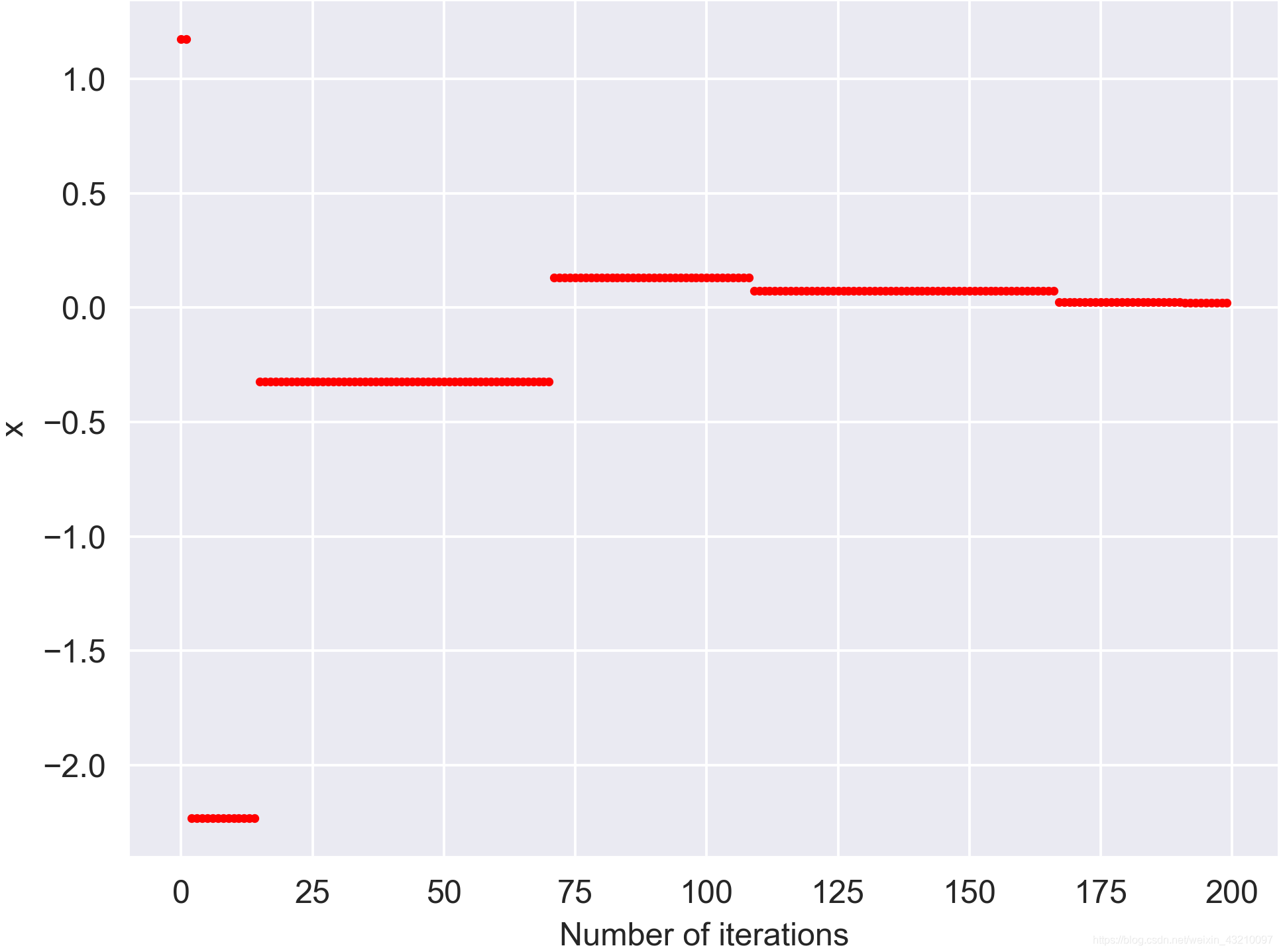
选取其中一个x反应变化规律:最开始有波动,最后稳定在0附近。
出于好奇,我将代码中君主交叉部分给注释掉了,其他地方不做修改。得到的结果如下所示:
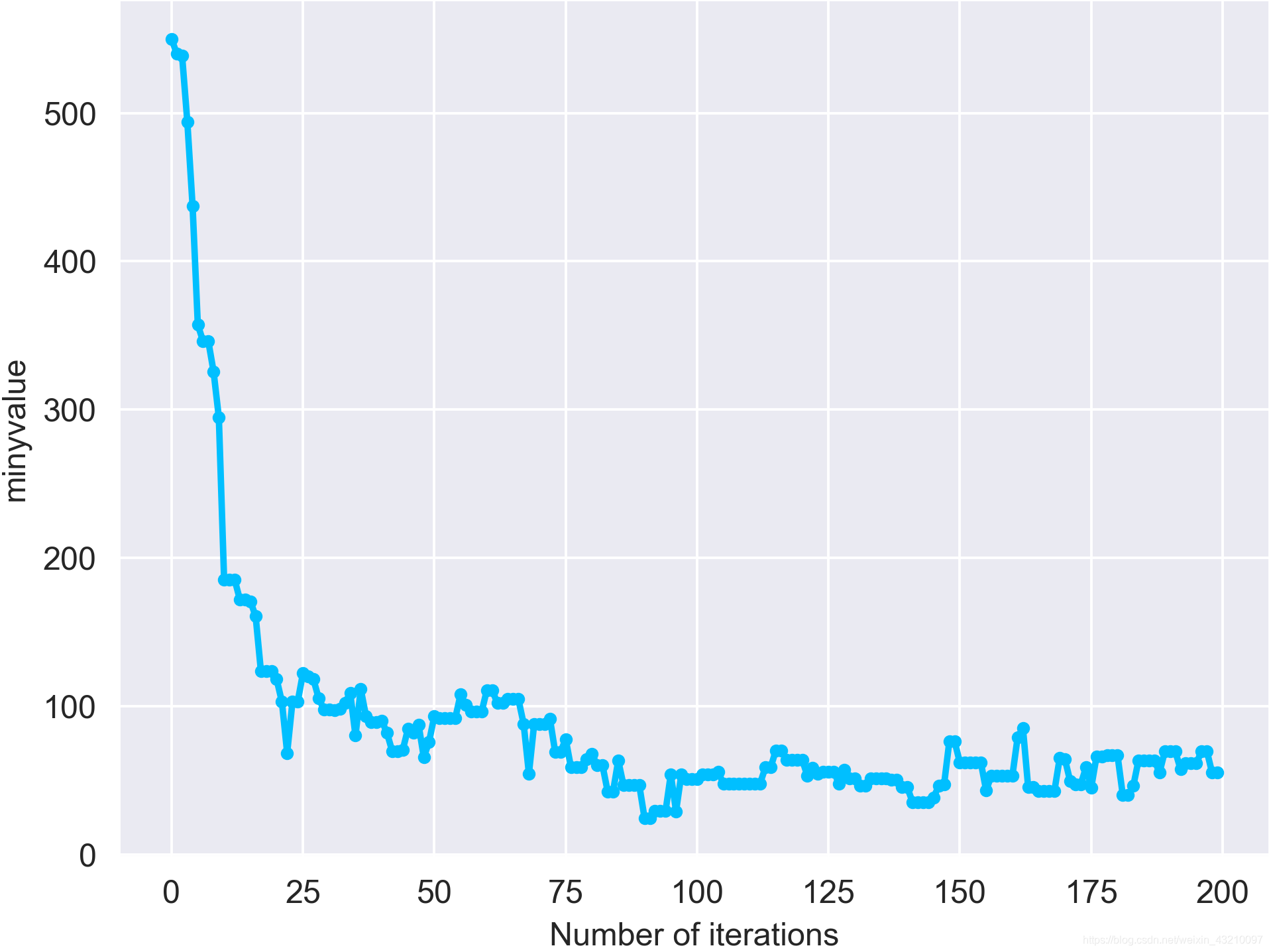
y的波动明显变大了,而且到200代的时候还未收敛。君主交叉还是很香的。君主交叉部分代码在代码展示部分有注释,需要的伙伴自己动手去试一下就ok了。
最后,推荐一个实现相同功能的Matlab代码链接(emmmm,不是我写的),需要的同学可以将Python和Matlab对比起来看。
https://blog.csdn.net/yangguangdblu/article/details/78816479





 本文介绍了一种改进的遗传算法,采用君主交叉和实数编码,用于寻找一组10维向量X,使其平方和最小。通过对比去除君主交叉后的效果,展示了该策略在加速收敛和稳定性上的优势。
本文介绍了一种改进的遗传算法,采用君主交叉和实数编码,用于寻找一组10维向量X,使其平方和最小。通过对比去除君主交叉后的效果,展示了该策略在加速收敛和稳定性上的优势。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








