计算顺序统计量，在 c++ 标准库中对应有一个函数：nth_element。其作用是求解一个数组中第 k 大的数字。常见的算法是基于 partition 的分治算法。不难证明这种算法的最坏复杂度是
Θ
(
n
2
)
\Theta(n^2)
Θ(n2)。但是其期望复杂度是
Θ
(
n
)
\Theta(n)
Θ(n) 。
另外，存在一种最坏复杂度是 Θ ( n ) \Theta(n) Θ(n) 的算法，其设计和证明思路比较有意思，拿来说一下。
基于 partition 的算法期望复杂度证明
求期望离不开随机变量。假设在 n 个元素的数组
A
[
p
.
.
.
q
]
A[p...q]
A[p...q] 上运行算法的时间是 T(n)。partition 算法会将 A 数组中元素等概率的选为主元并分割。定义指示器随机变量
X
k
=
{
分割后左半边数组的元素有正好有
k
个
}
X_k = \{分割后左半边数组的元素有正好有 k 个\}
Xk={分割后左半边数组的元素有正好有k个}
则有
E
(
X
k
)
=
1
/
n
×
1
+
(
n
−
1
)
/
n
×
0
=
1
/
n
E(X_k)=1/n × 1 + (n - 1) / n × 0 = 1 / n
E(Xk)=1/n×1+(n−1)/n×0=1/n
将 A 分为两部分后，算法会选择一边进行递归。为求得最坏情况，假设每次都从较长的一边进行递归，则有不等式
T
(
n
)
≤
∑
k
=
1
n
X
k
⋅
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
+
O
(
n
)
T(n) \le \sum_{k=1}^n X_k \cdot T(max(k-1, n - k)) + O(n)
T(n)≤k=1∑nXk⋅T(max(k−1,n−k))+O(n)
取期望得
E
(
T
(
n
)
)
≤
E
(
∑
k
=
1
n
X
k
⋅
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
]
+
O
(
n
)
E(T(n)) \le E(\sum_{k=1}^n X_k \cdot T(max(k-1, n - k))] + O(n)
E(T(n))≤E(k=1∑nXk⋅T(max(k−1,n−k))]+O(n)
根据事件间独立性和线性关系，得
E
(
T
(
n
)
)
≤
∑
k
=
1
n
E
(
X
k
)
⋅
E
(
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
)
]
+
O
(
n
)
=
1
n
∑
k
=
1
n
E
(
T
(
m
a
x
(
k
−
1
,
n
−
k
)
)
)
]
+
O
(
n
)
E(T(n)) \le \sum_{k=1}^n E(X_k) \cdot E(T(max(k-1, n - k)))] + O(n) \\ = \frac{1}{n} \sum_{k=1}^n E(T(max(k-1, n - k)))] + O(n)
E(T(n))≤k=1∑nE(Xk)⋅E(T(max(k−1,n−k)))]+O(n)=n1k=1∑nE(T(max(k−1,n−k)))]+O(n)
取较大的边进行缩放，得到
E
(
T
(
n
)
)
≤
2
n
∑
k
=
n
/
2
n
E
[
T
(
k
)
]
+
O
(
n
)
E(T(n)) \le \frac{2}{n} \sum_{k=n/2}^n E[T(k)] + O(n)
E(T(n))≤n2k=n/2∑nE[T(k)]+O(n)
用代入法来证明 E ( T ( n ) ) = O ( n ) E(T(n)) = O(n) E(T(n))=O(n)，假设 E ( T ( n ) ) ≤ c n E(T(n)) \le cn E(T(n))≤cn，代入公式右半边，同时为方便说明，选择常数 a 代入 O(n) 中
E
(
T
(
n
)
)
≤
2
n
∑
k
=
n
/
2
n
c
k
+
a
n
=
2
n
⋅
3
n
/
2
×
n
/
2
2
+
a
n
=
3
c
n
4
+
a
n
=
(
3
c
+
4
a
)
n
4
E(T(n)) \le \frac{2}{n} \sum_{k=n/2}^n ck + an \\ = \frac{2}{n} \cdot \frac{3n/2 × n/2}{2} + an\\ = \frac{3cn}{4} + an\\ =\frac{(3c + 4a)n}{4}
E(T(n))≤n2k=n/2∑nck+an=n2⋅23n/2×n/2+an=43cn+an=4(3c+4a)n
只要选取较大得常数 c 即可满足
E
(
T
(
n
)
)
≤
c
n
E(T(n)) \le cn
E(T(n))≤cn，方式如下，令
(
3
c
+
4
a
)
n
4
≤
c
n
\frac{(3c + 4a)n}{4} \le cn
4(3c+4a)n≤cn
得
c
≥
16
a
c \ge 16a
c≥16a
证明完毕，期望复杂度是
Θ
(
n
)
\Theta(n)
Θ(n)
最坏情况下是线性的算法
该算法常数比较大，先描述一下基本原理
第一步，找到一个特别的中位数
- 将数组每 5 个元素分为一组
- 每组分别排序，找到 n / 5 个中位数
- 将这 n / 5 个中位数，递归调用本算法，找到其中位数 x
至此找到了一个特别的中位数的中位数 x
第二步，划分 - 使用 x 对数组进行划分。设 x 是第 k 小的数
- 如果 k = i 则结束，否则根据情况在低区或者高区来进行递归调用
证明：
首先分析这个特殊的中位数的中位数 x 的性质。可以知道，在数组中，至少有
3
n
10
−
6
\frac{3n}{10}-6
103n−6个元素大于 x，同理有至少有
3
n
10
−
6
\frac{3n}{10}-6
103n−6 个元素小于 x。也就是说，第5步的最坏情况，递归调用作用在
7
n
10
+
6
\frac{7n}{10}+6
107n+6个元素上。现在可以设计递推式。
步骤1 2 4 总共需要 O(n) 的复杂度，步骤 3 需要时间为 T(n / 5)，步骤 5 需要时间最多为
T
(
7
n
10
+
6
)
T(\frac{7n}{10}+6)
T(107n+6)，因此有
T
(
n
)
≤
T
(
n
/
5
)
+
T
(
7
n
/
10
+
6
)
+
O
(
n
)
T(n) \le T(n / 5) + T(7n/10 + 6)+ O(n)
T(n)≤T(n/5)+T(7n/10+6)+O(n)
再次使用替换法。假设 某个适当大的常数 c 满足
T
(
n
)
≤
c
n
T(n) \le cn
T(n)≤cn，某个常数 a 来表示 公式中 O(n) 的上界。则有
T
(
n
)
≤
c
n
/
5
+
7
c
n
/
10
+
6
c
+
a
n
T(n) \le cn/5 + 7cn/10 + 6c + an\\
T(n)≤cn/5+7cn/10+6c+an
为挑选出足够大的 c 列出如下不等式，若如下不等式成立，则找到了足够大的 c
c
n
/
5
+
7
c
n
/
10
+
6
c
+
a
n
≤
c
n
−
n
c
/
10
+
6
c
+
a
n
≤
0
cn/5 + 7cn/10 + 6c + an \le cn\\ -nc/10 + 6c+an\le0
cn/5+7cn/10+6c+an≤cn−nc/10+6c+an≤0
当
n
>
60
n \gt 60
n>60时有如下变换
c
≥
10
a
n
/
(
n
−
60
)
c \ge 10an/(n-60)
c≥10an/(n−60)
函数图像大致如下
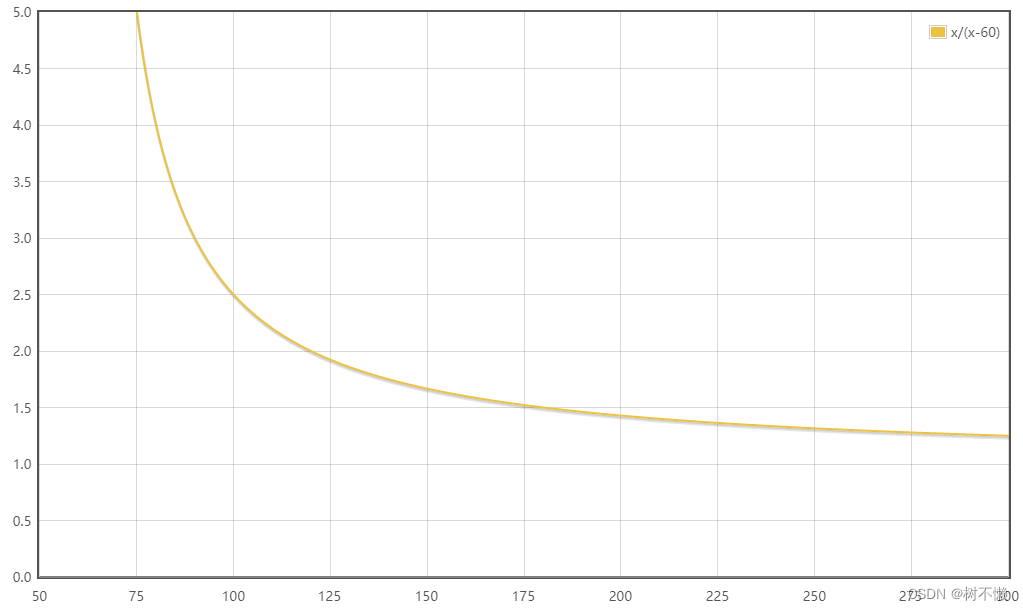因此 不妨设
n
≥
120
n \ge 120
n≥120 , 有
n
/
(
n
−
60
)
<
2
n/(n - 60) < 2
n/(n−60)<2，即
c
≥
20
a
,
n
≥
120
c \ge 20a, n \ge120
c≥20a,n≥120
结果合并如下
T
(
n
)
≤
{
O
(
1
)
,
n
<
120
O
(
n
)
,
n
≥
120
T(n) \le \begin{cases} O(1), n < 120 \\ O(n), n \ge 120 \end{cases}
T(n)≤{O(1),n<120O(n),n≥120
证毕
1102
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
