知识点
[记录本章包含哪些内容]
未攻克
[记录还不会的知识点]
笔记
数制与编码
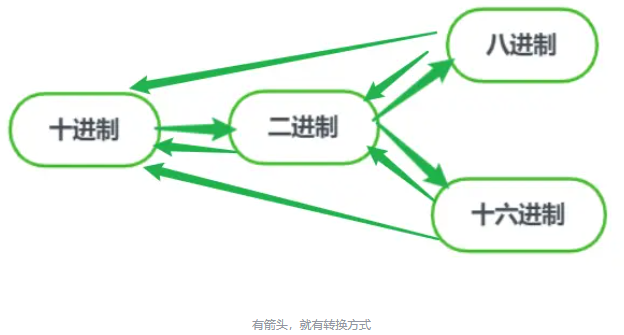
进制之间的转换小结
进位计数制
- 字节是最基本的信息单位【B】
- 位是最小的信息单位【bit】
- 1 字节【B】=8 位【bit】
- 基数:每个数码位所用到的不同符号的个数,r 进制的基数为 r
- 位权:由位置确定的权重,如: 975.36 = 9 ∗ 1 0 2 + 7 ∗ 1 0 1 + 5 ∗ 1 0 0 + 3 ∗ 1 0 − 1 + 6 ∗ 1 0 − 2 975.36=9*10^2+7*10^1+5*10^0+3*10^{-1}+6*10^{-2} 975.36=9∗102+7∗101+5∗100+3∗10−1+6∗10−2
常用进制:
- 二进制:0,1 二进制转十进制: 101.1 − > 1 ∗ 2 2 + 0 ∗ 2 1 + 1 ∗ 2 0 + 1 ∗ 2 − 1 = 5.5 101.1->1*2^2+0*2^1+1*2^0+1*2^{-1}=5.5 101.1−>1∗22+0∗21+1∗20+1∗2−1=5.5 , (B 表示二进制)
- 八进制:0,1,2,3,4,5,6,7 (O 表示八进制)
- 十进制:0,1,2,3,4,5,6,7,8,9(除了符号反映权重外,符号所在位置也反映权重)(可表示为: 165 2 10 = 1652 D 1652_{10}=1652D 165210=1652D)
- 十六进制:0,1,2,3,4,5,6,7,8,9,A, B, C, D, E, F (可表示为: 165 2 16 = 1652 H = 0 x 1652 1652_{16}=1652H=0x1652 165216=1652H=0x1652
二进制、八进制、十六制均与十进制加法类似,均是逢二进一,八进一、十六进一
- 二进制是最适合计算机存储和处理的计数方式,①可使用两个稳定状态的物理器件表示,②0,1 正好对应逻辑值假、真。方便实现逻辑运算,③可很方便的使用逻辑门电路实现算术运算

二进制转八进制
3 位一组,每组转换成对应的八进制符号
示例:1111000010.01101 --> 001 111 000 010.011 010 (位数不够添 0,也就是补位) -->1702.32 (八进制)

二进制转十六进制
4 位一组,每组转换成对应的十六进制符号
示例:1111000010.01101–> 0011 1100 0010.0110 1000 --> 3C2.68 (十六进制)
八进制转二进制
每位八进制对应的 3 位二进制
示例: ( 251.5 ) 8 − > ( 010101001.101 ) 2 (251.5)_8 -> (010 101 001.101)_2 (251.5)8−>(010101001.101)2
十六进制转二进制
每位十六进制对应的 4 位二进制
示例: ( A E 86.1 ) 16 − > ( 101011100110.0001 ) 2 = 1010001010010 B (AE86.1)_{16} -> (1010 1110 0110.0001)_2 = 1010001010010B (AE86.1)16−>(101011100110.0001)2=1010001010010B
十进制转任意进制

step1 称为除基取余法,对整数部分的处理;step2 称为乘基取整法,是对小数部分的处理
- 精度不够的时候用 2 个点表示,如:0.3D=0.01001… B(此时精度为 5)

【补充:】
- 十六进制数转为八进制数(或八进制数转换为十六进制数)时,先将十六进制(八进制)数转换为二进制数,然后由二进制数转换为八进制(十六进制)数比较方便
- 小数是离散的,所以并不是每个十进制小数都可以准确的用二进制表示(如 0.3),但任意一个二进制小数都可以用十进制小数表示
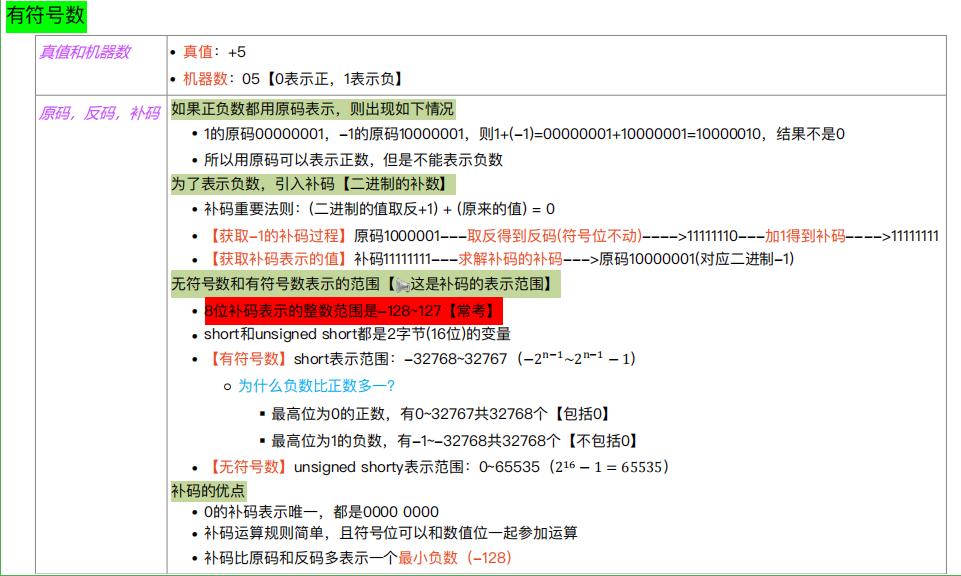
真值和机器数
- 真值:实际的带正负号的数值(人类习惯的样子)–机器数所代表的实际值
- 机器数:数字实际存到机器里的形式(把正负号数字化的数)
定点数的编码表示
在现代计算机中,通常用补码整数表示整数,用原码小数表示浮点数的尾数部分,用移码表示浮点数的阶码部分
- 浮点数:小数点的位置不固定,eg: 9.96007 ∗ 1 0 2 9.96007*10^2 9.96007∗102 --科学计数法
- 定点数:小数点的位置固定,eg: 996.007 996.007 996.007 --常规计数
定点数分为无符号数和有符号数,有符号数可以用原码、反码、补码、移码表示。
无符号数与有符号数:不改变数据内容、改变解释方式
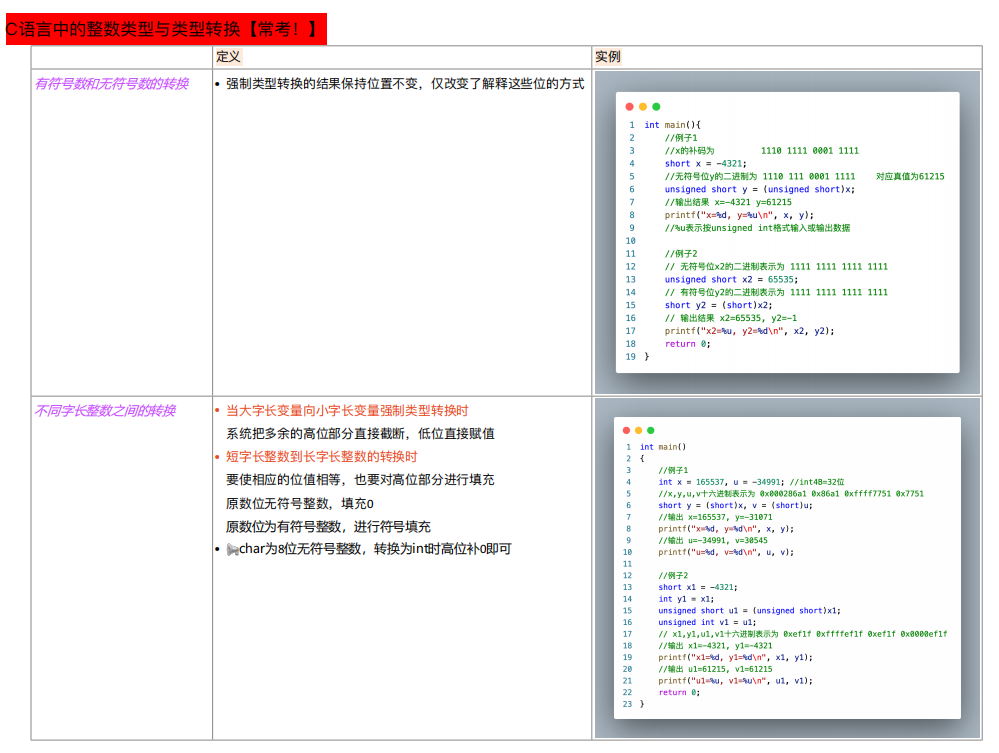
C 语言中的长整数(int 型,占用 4 个字节)变短整型(short 型,占用 2 个字节)高位截断,保留低位
C 语言中短整型变长整型:符号扩展
unsigned ()修饰的整数为无符号整数,可强制转换有符号数和无符号数之间的转换,
有符号数转换为等长的无符号数时,强制类型转换的结果是保持位值不变,仅改变了解释这些位的方式;负数转换为无符号数时数值将发生变化。同理,无符号数转换为有符号数时最高位解释为符号位,也可能发生数值的变化
无符号数
- 无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值
- 寄存器的位数决定了无符号数的表示范围。如 8 位寄存器,无符号数表示范围为 0~255
- 表示范围:8 位(bit)无符号数的范围:0~255= 2 8 − 1 2^8-1 28−1,16 位无符号数的范围:0~65535
推广:n 位的无符号数表示范围:0 ~ 2 n − 1 2^n- 1 2n−1- 谈到无符号数时通常只有无符号整数,而没有无符号小数
- 用无符号数表示主存地址
有符号数
- 分定点整数和定点小数
【注】可用原码、反码、补码三种方式来表示定点整数和定点小数。还可用移码表示定点整数。若真值为 x x x,则用 [ x ] 原 [x]_原 [x]原、 [ x ] 反 [x]_反 [x]反 、 [ x ] 补 [x]_补 [x]补 、 [ x ] 移 [x]_移 [x]移 分别表示真值所对应的原码、反码、补码、移码。
码之间的转换
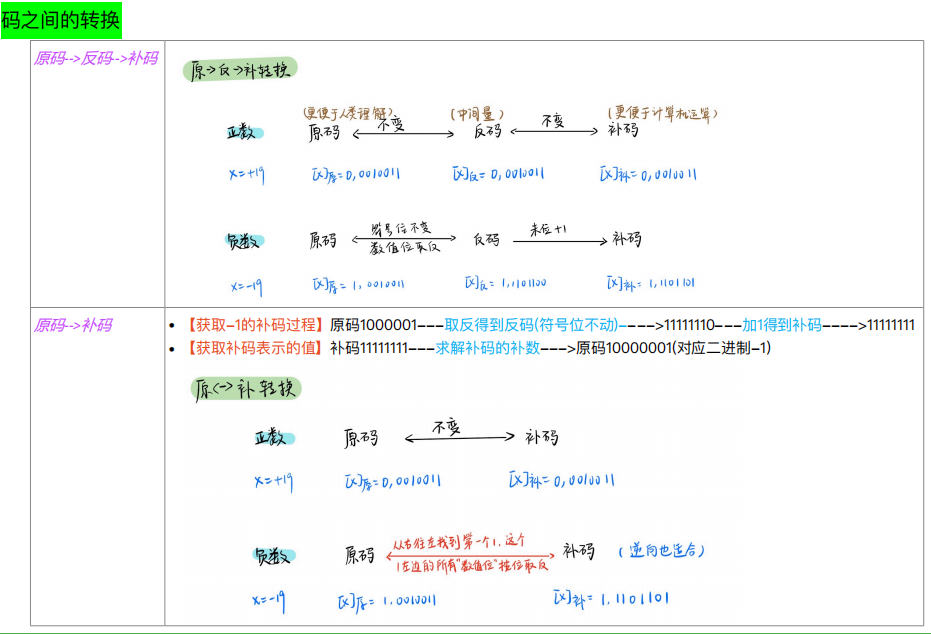
1. 原码
原码表示法:

用尾数表示真值的绝对值,符号位“0/1”,对应“正/负”
若机器字长 n+1 位,则尾数占 n 位。
定点整数表示:常写为: [ x ] 原 = 1 , 0010011 [x]_原=1,0010011 [x]原=1,0010011,若未指明机器字长,也可写为: [ x ] 原 = 1 , 10011 [x]_原=1,10011 [x]原=1,10011
- 若机器字长 n+1 位,原码整数的表示范围: − ( 2 n − 1 ) ≤ x ≤ 2 n − 1 -(2^n-1)≤x≤2^n-1 −(2n−1)≤x≤2n−1 (关于原点对称) 。
- 真值 0 有+0 和-0 两种形式
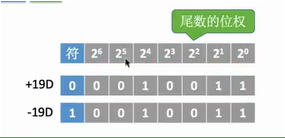
定点小数表示:常写为: [ x ] 原 = 1.1100000 [x]_原=1.1100000 [x]原=1.1100000
- 若机器字长 n+1 位,原码小数的表示范围: − ( 1 − 2 − n ) ≤ x ≤ 1 − 2 − n -(1-2^{-n})≤x≤1-2^{-n} −(1−2−n)≤x≤1−2−n (关于原点对称)
- 真值 0 有+0 和-0 两种形式
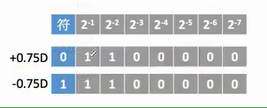
常写为中的点和逗号之前的数 1,0 表示正负,定点小数中的点非小数点
📕原码表示的优缺点:
优点:①与真值的对应关系简单直观,与真值的转换简单;②用原码实现乘除比较简便
缺点:①0的表示不唯一,有±0两个编码,②原码加减法运算比较复杂.在原码加减法运算中,对于两个不同符号数的加法(或同符号数的减法),先要比较两个数的绝对值大小,然后用绝对值大的数减去绝对值小的数,最后还要为结果选择合适的符号.
2. 反码(先得到原码再得到反码)
- 若符号位为 0,则反码与原码相同;若符号位为 1,则数值位全部取反(01 互换)
- 反码的表示范围与原码一致
- “反码”只是“原码”转变为“补码”的一个中间状态,实际中无用
反码表示存在以下几个方面的不足:① 0的表示不唯一,存在±0,②表示范围比补码少一个最小负数;反码在计算机中很少使用,通常用作数码变换的中间表示形式
3. 补码
- 补码表示法中的加减运算统一采用加法操作实现
- 计算机中的有符号整数都用补码表示
- 正数的补码=原码
- 负数的补码=反码末位+1(要考虑进位)
- 补码的真值 0 只有一种表示形式
- 定点整数补码 [ x ] 补 = 1 , 0000000 [x]_补=1,0000000 [x]补=1,0000000 表示为 x = − 2 7 x=-2^7 x=−27
- 若机器字长 n+1 位,补码整数的表示范围: − 2 n ≤ x ≤ 2 n − 1 -2^n≤x ≤2^n-1 −2n≤x≤2n−1 (比原码多表示一个 − 2 n -2^n −2n)
- 定点小数补码 [ x ] 补 = 1.0000000 [x]_补=1.0000000 [x]补=1.0000000 表示为 x = − 1 x=-1 x=−1
- 若机器字长 n+1 位,补码小数的表示范围: − 1 ≤ x ≤ 1 − 2 − n -1≤x ≤1-2^{-n} −1≤x≤1−2−n (比原码多表示一个 − 1 -1 −1)
- 将负数补码转回原码的方法相同,尾数取反,末尾+1
- 【补码作用】:使用补码可将减法操作转变为等价的加法,ALU 中无需集成减法器,执行加法操作时,符号位一起参与运算
- 在(mod m)的条件下,若能找到负数的补数,就可以用正数的加法来等价替代减法 模 − a 的绝对值 = a 的补数 模-a的绝对值=a的补数 模−a的绝对值=a的补数

补码的表示:

真值转换为补码:对于正数,与原码的方式一样. 对于负数,符号位取1,其余各位由真值"各位取反,末位加1"得到
补码转换为真值:若符号位为0,与原码的方式一样;若符号位为1,真值的符号为负,数值部分各位由补码“各位取反,末位加1”得到
4. 移码
- 补码的基础上将符号取反。【注】移码只能用于表示整数
- 补码的真值 0 只有一种表示形式
- 移码的表示范围与补码一致
- 移码定义: [ x ] 移 = 2 n + x ( − 2 n ≤ x ≤ 2 n ,其中机器字长为 n + 1 ) [x]_移=2^n+x (-2^n≤x≤2^n,其中机器字长为n+1) [x]移=2n+x(−2n≤x≤2n,其中机器字长为n+1) ,如: x 1 = + 10101 , x 2 = − 10101 x_1=+10101,x_2=-10101 x1=+10101,x2=−10101,机器字长为 8 为,则其移码为 [ x 1 ] 移 = 2 7 + 10101 = 1 , 0010101 ; [ x 2 ] 移 = 2 7 + ( − 10101 ) = 0 , 1101011 [x_1]_移=2^7+10101=1,0010101;[x_2]_移 = 2^7+(-10101)=0,1101011 [x1]移=27+10101=1,0010101;[x2]移=27+(−10101)=0,1101011
- [ + 0 ] 移 = [ − 0 ] 移 = 10000000 [+0]_移=[-0]_移=10000000 [+0]移=[−0]移=10000000
- ==【移码作用】 ==移码表示的整数很方便计算机对比大小
📕移码特点:
- 移码中零的表示唯一
- 一个真值的移码和补码仅差一个符号位,补码的符号位取反得到移码(1 表示正,0 表示负,与其他机器数的符号位取值正好相反),反过来也可以
- 移码全 0 时,对应真值的最小值 − 2 n -2^n −2n ;移码全 1 时,对应真值的最大值 2 n − 1 2^n-1 2n−1
- 移码保持了数据原有的大小顺序,移码大真值就大,移码小真值就小
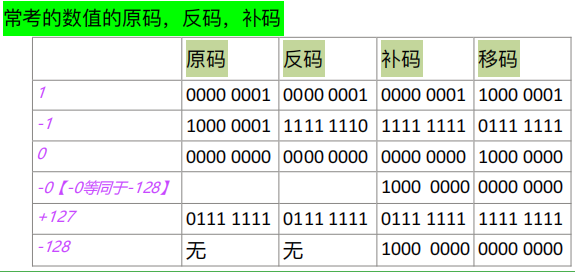
📕原码、补码、反码和移码总结:
- 原码、补码、反码的符号位相同,正数的机器码相同
- 原码、反码的表示在数轴上对称,两者都存在+0 和-0 两个 0
- 原码和反码的真值有两种表示
- 补码和移码的表示在数轴上不对称,零的表示唯一,它们比原码、反码多表示一个数
- 补码和移码的真值只有一种表示
- 补码和移码可以多表示一个负数
- 整数的补码、移码的符号位相反,数值位相同
- 负数的补码、反码末位相差 1
- 原码很容易判断大小。而负数的补码、反码很难直接判断大小,可采用如下规则快速判断:对于负数,数值位部分越小,其绝对值越大,即负的越多
- 求各种码对应的真值,先将各种码转换为源码
- C 语言中定点整数是用“补码”存储的
- 【技巧】:由 [ x ] 补 [x]_补 [x]补 快速求 [ − x ] 补 [-x]_补 [−x]补 的方法:符号位、数值位全部取反,末位+1
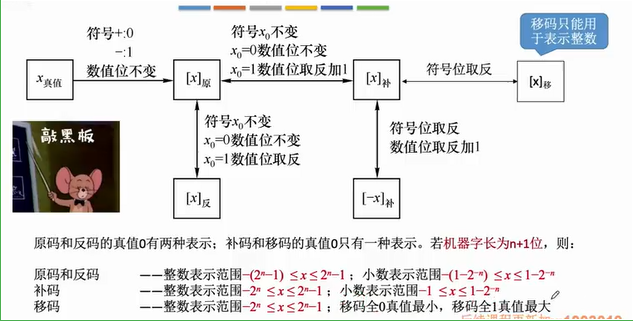
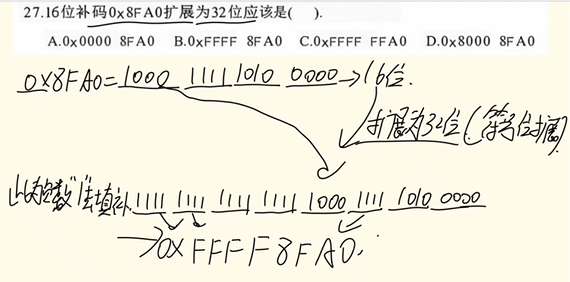
对数据进行长度扩展
长度扩展原因:
- ALU 的位数是固定的,运算前可能需要把短数据扩展为长数据
- 通用寄存器位数是固定的,把数据存入寄存器时,可能需要进行长度扩展
- 主存内的各种数据长度不一,有时需要把短数据扩展为长数据
扩展方法:零扩展和符号扩展
无符号整数用零扩展,高位用 0 填充;带符号整数用符号扩展,多出来的位用“符号位”填充

小节选择题答案
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 答案 | B | B | D | B | B | D | C | C | A | C | C | |
| 序号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 答案 | C | A | D | B | D | |||||||
| 序号 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | ||
| 答案 | D | D | A | A | B | A | D | A | B |
该小节习题不顺畅
错题序号汇总:8、9、10、12-24、27-30、32-33
有的题不会,但蒙对了
错题汇总:
- 十进制转八进制方法:①整数部分除基取余法 KaTeX parse error: Undefined control sequence: \ce at position 1: \̲c̲e̲^,小数部分乘基取整法 ↓ \downarrow ↓,②排除法:从选项的八进制转十进制对比(会比较快)八进制转十进制方法:整数部分位数8 的 0-… 方,小数部分位数乘以8 的-n 次方
- 题目中说明 n+1 位,二进制数的表示范围:

2 15 = 32768 , 2 16 = 65536 2^{15}=32768,2^{16}=65536 215=32768,216=65536
- 说法正确的是:
- 任何二进制整数都可以用十进制表示
- 任何二进制小数都可以用十进制表示
- 任何十进制整数都可以用二进制表示
错误说法:任何十进制小数都可以用二进制表示(x),如 0.3
-
真值 0 在原码、反码、补码、移码中的最大数、最小数和表现形式:

记住 -
给补码互求原码:方法① 符号位不变,数值位全部取反,末位加 1,②从右往左,找到第一个 1,1 之前的数值全部取反直接得到原码

-
由 [ x ] 补 [x]_补 [x]补 求 [ − x ] 补 [-x]_补 [−x]补,通常在补码减法使用(减法转加法): [ A ] 补 − [ B ] 补 = [ A ] 补 + [ − B ] 补 [A]_补-[B]_补 = [A]_补+[-B]_补 [A]补−[B]补=[A]补+[−B]补
[ B ] 补 [B]_补 [B]补 互转 [ − B ] 补 [-B]_补 [−B]补 的方法:全部位按位取反(包含符号位),末位加 1 -
8 位原码能表示的不同数据有几个:
法①:8 个二进制数有 2 8 = 256 2^8=256 28=256 种表示方法,但在原码和反码中 0 有两种表示,故应为 255 种, 2 8 − 1 2^8-1 28−1
法②:原码对于 n+1 位,取值范围为 − ( 2 n − 1 ) ≤ x ≤ 2 n − 1 -(2^n-1)≤x≤2^n-1 −(2n−1)≤x≤2n−1 -
D

-
A

-
给位数 64,采用补码表示的的绝对值最大的负数为:
- 绝对值最大,则为最小的负数
- C
- B
正确说法
- 相同位数的补码和移码表示具有相同的数据表示范围
- 同一个数的补码和移码表示,其数值部分相同,而符号相反
- 一般用移码表示浮点数的阶码,而补码表示定点整数
13:给定 x 的补码 [ x ] 补 = 1 , x 1 x 2 x 3 x 4 x 5 x 6 [x]_补=1,x_1x_2x_3x_4x_5x_6 [x]补=1,x1x2x3x4x5x6,要求 x>-32,数值位应满足什么条件?
- 需要补码转为原码,也可由补码直接算出真值,如补码 1,101000,对应真值 = 1 ∗ 2 3 + 1 ∗ 2 5 + ( − 1 ) ∗ 2 6 = 8 + 32 − 64 = − 24 =1*2^3+1*2^5+(-1)*2^6=8+32-64=-24 =1∗23+1∗25+(−1)∗26=8+32−64=−24
- C
法①: x 6 ∗ 2 0 + x 5 ∗ 2 1 + x 4 ∗ 2 2 + x 3 ∗ 2 3 + x 2 ∗ 2 4 + x 1 ∗ 2 5 + ( − 1 ) ∗ 2 6 > − 32 x_6*2^0+x_5*2^1+x_4*2^2+x_3*2^3+x_2*2^4+x_1*2^5+(-1)*2^6>-32 x6∗20+x5∗21+x4∗22+x3∗23+x2∗24+x1∗25+(−1)∗26>−32 - 由选项倒推
法②:选项逐项看

14 题做法同 13 题,
-
D

-
B

-
C
- H 表示 16 进制,4 位一组

- A
- D

20 和 21题和 19 题做法类似,由数值倒推,补码和移码仅相差一个符号位,还可用排除法,给定寄存器内容 0 开头,是一个正数,而正数的原码、补码、反码是一致的,若 A 对则 BC 都对
- C
- 给二进制定点小数真值为 -0.1101,机器表示 1.0010,问是原、反、补移码中的哪一个

- B
- 溢出,其实就是在问谁落在了最大范围之外

- 补码的最小数表示为:10000000,移码的最小数表示为:00000000
- A #todo暂未理解
- 选项中的偏置值需要转换为机器数
- 移码-偏置值=真值,减的时候直接当作正常的减法即可,符号位也减
- D
- 符号位不但可以表示符号还可用表示数值
- 原码才和真值的对应关系简单、直接,补码还需要转换为原码才可以得出真值
- 在计算机中,通常用来表示主存地址的是无符号数,主存地址一般用正数来表示
-
B
-
B
- 从数字出发

- D #todo暂未理解
- 有符号短整型转无符号短整型,从数字出发

- A
- 无符号短整型转有符号短整型,无符号说明所有位都是数值位
- 机器数一般用补码表示

- D

运算方法和运算电路
运算
- 有算术运算和逻辑运算
- 无论是算术运算还是逻辑运算都一定会有输入和输出
逻辑门运算
- 在逻辑运算中,1 为真,0 为假
- 逻辑运算的对象不是数值,因此不会出现进位的情况
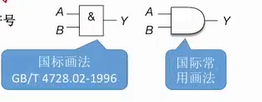
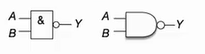
📕与运算 AND
- 表达式:Y=A ·B,也可简写为 Y=AB
- A 和 B 同时为真时,Y 为真
- 门电路图形符号(关注国际画法即可)
- A 和 B 为输入,Y 为输出
📕或运算 OR
- 表达式:Y=A+B
- A 和 B 同时为假时,Y 为假
- 门电路图形符号
📕 非运算 NOT
- 表达式:
- 只有一个输入,输入为 1,输出为 0;输入为 0,输出为 1
- 门电路图形符号
📕与非 NAND
- 表达式:
- 两个输入,先进行与运算,再取反,A 和 B 同时为 1 时,Y 为 0
- 门电路图形符号
📕或非 NOR
- 在或的表达式头加一横
- 两个输入,先进行或运算再取反,A 和 B 同时为 1 时,Y 为 0;A 和 B 同时为 0 时,Y 为 1,其余为 0
- 门电路图形符号
📕异或 XOR
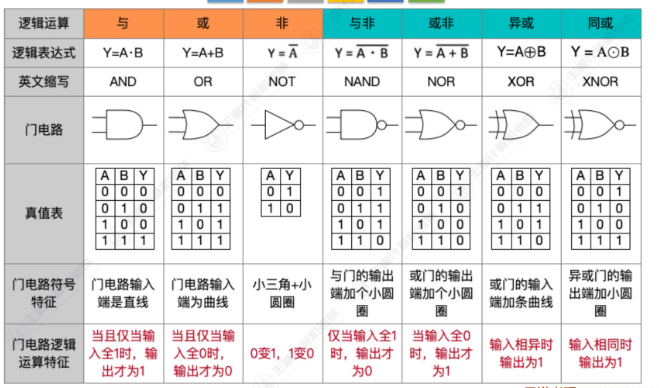
- 表达式:
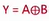
- 两个输入相"异"时,输出为 1,其余为 0
- 门电路图形符号
- n bit 进行异或,若有奇数个 1,则异或结果为 1;若有偶数个 1,则异或结果为 0
“封装”思想:屏蔽电路部件的内部实现细节,仅对外暴露输入/输出引脚。使用者仅需关心该部件的功能即可
📕同或 XBOR
- 表达式:
- AB 两个输入相“同“时,输出为 1,其余为 0
- 门电路图形符号,有的地方也会称为"异或非门"
逻辑门电路基础总结
- 三种基本逻辑运算的优先级:非>与>或
- 括号会提升运算的优先级,有括号先算括号
- 非运算符下面,可理解为“隐含一个括号”
本质上逻辑表达式是对电路的数学化描述,简化逻辑表达式,就是在简化电路设计,就是在省钱
门电路由“晶体管”实现
基本运算部件
- 在计算机中,运算器由算术逻辑单元(ALU)、移位器、状态寄存器(PSW)和通用寄存器组等组成
- 运算器的基本功能包括加、减、乘、除四则运算,与、或、非、异或等逻辑运算,以及移位、求补等操作
- ALU 的核心部件为加法器,ALU 是运算器的核心
加法器
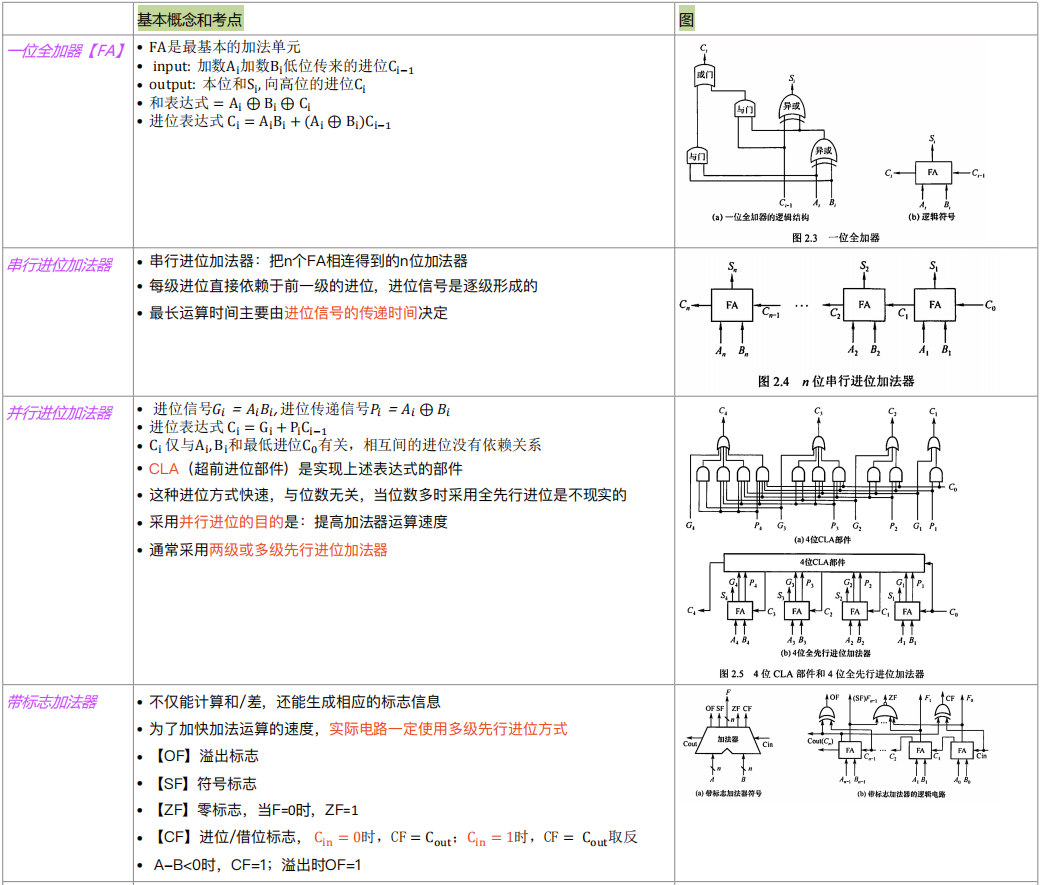
算术逻辑单元 ALU
- ALU 是一种功能较强的组合逻辑电路,能进行多种算术运算和逻辑运算
- ALU 的核心是带标志加法器,同时也能执行“与”“或”“非”等逻辑运算
- ALU 的基本结构:
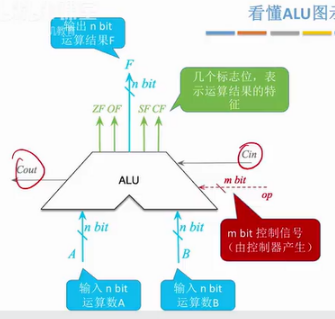
- A 和 B 是两个 n 位操作数输入端
- Cin 是进位输入信号、Cout 是进位输出信号(类似于带标志位的加法器)
- ALUop 是操作控制端(发出控制信号),用来决定 ALU 所执行的处理功能。op 的位数决定了操作的种类,比如位数为 3 时,ALU 最多只有 8 种操作
考试重点:
- 如果 ALU 支持 k 种功能,则控制信号位数 m ≥ [ l o g 2 k ] m≥[log_2k] m≥[log2k]
- ALU 的运算数、运算结果位数与计算机的机器字长相同
- ZF/OF/SF/CF 标志位,用于表示本次运算结果的特征(ZF 表示运算结果是否为零、OF 表示有符号数运算结果是否溢出、SF 表示有符号数运算结果的正负性、CF 表示无符号数运算结果是否溢出)
- 这些标志信息通常会被送入 PSW 程序状态字寄存器【注🧨】有的计算机系统把 PSW 寄存器称为“标志寄存器 FR”
定点数的移位运算
- 移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法
- 根据操作数的类型不同,移位运算可以分为逻辑移位和算术移位
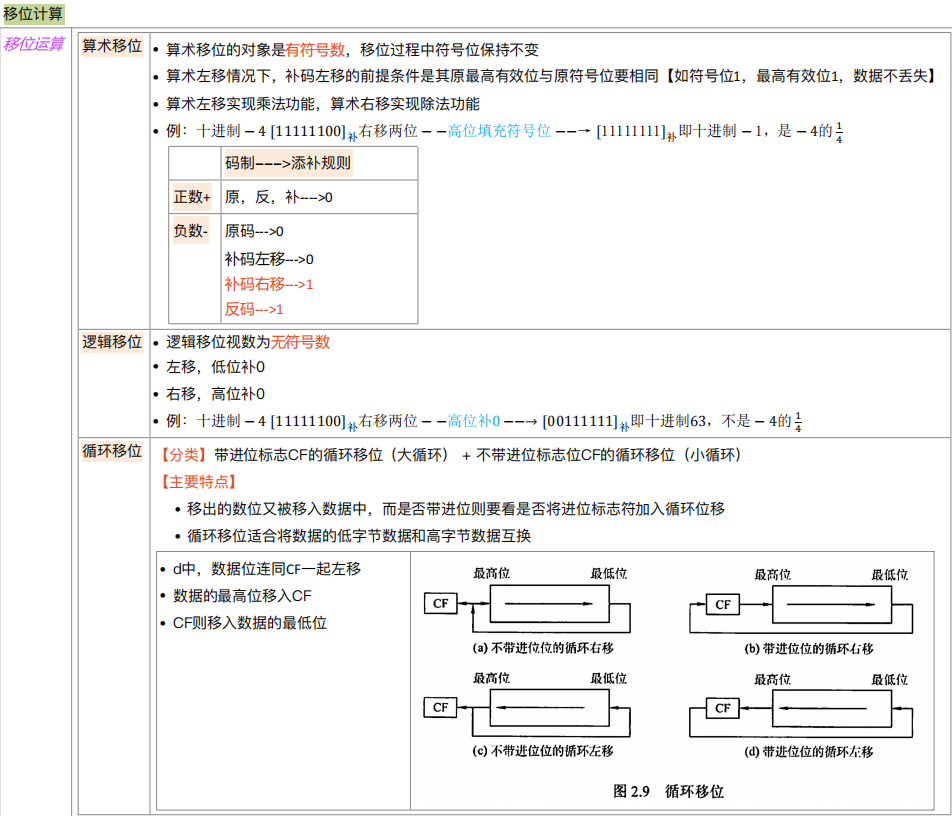
逻辑移位
- 逻辑移位将操作数视为无符号整数。
- 规则:
逻辑右移:高位补 0,低位舍弃
逻辑左移:低位补 0,高位舍弃
- 对无符号整数的逻辑左移,若高位的 1 移除,则发生溢出
算术移位
- 算术移位需要考虑符号位的问题,即将操作数视为有符号整数
- 计算机种的有符号整数都是用补码表示的,因此对于有符号整数的移位操作应采用补码算术移位的方式
- 规则:
原码的算术移位:-- 符号位保持不变,仅对数值位进行移位
- 右移:高位补 0,低位舍弃。若舍弃的位=0,则相当于➗2;若舍弃的位≠0,则会
丢失精度 - 左移:低位补 0,高位舍弃。若舍弃的位=0,则相当于✖2;若舍弃的位≠0,则会出现
严重误差
反码的算术移位:
- 正数的反码与原码相同
- 右移:高位补 0,低位舍弃
- 左移:低位补 0,高位舍弃
- 负数的反码数值位与原码相反
- 右移:高位补 1,低位舍弃
- 左移:低位补 1,高位舍弃
补码的算术移位:
- 正数的补码与原码相同
- 右移:高位补 0,低位舍弃
- 左移:低位补 0,高位舍弃
- 负数补码=反码末位+1 导致反码最右边几个连续的 1 都因进位而变为 0,直到进位碰到第一个 0 为止
规律--负数补码中,最右边的1及其右边同原码,最右边的1的左边同反码
- 右移(同反码):高位补 1,低位舍弃
- 左移(同原码):低位补 0,高位舍弃
总结
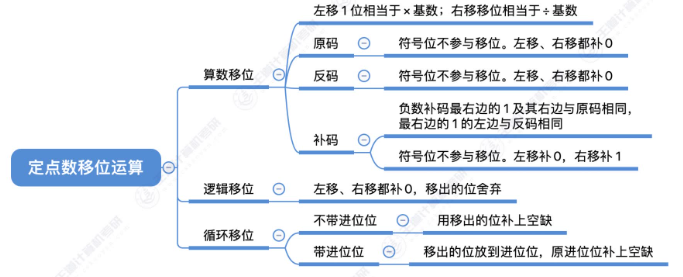
【注🧨】由于原、反、补码位数有限,因此某些时候算数移位不能精确等效乘法、除法
定点数的加减运算
- 原码的加减法运算规则比较复杂,因此计算机采用的大多是补码加减运算
- 带符号数都会转换为补码

原码的加减法运算(了解)
加法 – “同号求和,异号求差”
- 同号相加:数值部分=被加数、加数的绝对值进行相加,符号位不变
- 异号相加:数值部分=被加数、加数中,绝对值更大的减绝对值更小的,符号位与绝对值更大的数相同
减法
- 将减数取负,转变为加法
补码的加减法运算
- 符号位参与加法运算;减法要转变成等价的加法
- 【注🧨】已知【Y】补码,如何求【-Y】补码?—将【Y】补码全部位取反,末位+1
补码运算的特点:
- 按二进制运算规则运算,逢二进一
- 若做加法,两个数的补码直接相加;若做减法,则将被减数与减数的负数补码相加
- 符号位与数值位一起参与运算,加、减运算结果的符号位也在运算中直接得出
- 最终运算结果的高位丢弃,保留 n+1 位,运算结果亦为补码
溢出判断(补码)
仅当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出,
Key: 正+正=负(上溢),负+负=正(下溢)
- 采用一位符号位
由于减法运算在机器中是用加法器实现的,因此无论是加法还是减法,只要参加操作的两个数的符号相同,结果又与原操作数的符号不同,则表示结果溢出
设 A 的符号为
A
s
A_s
As,B 的符号为
B
s
B_s
Bs,运算结果的符号为
S
s
S_s
Ss,则溢出逻辑表达式为:
V
=
A
s
B
s
S
s
‾
+
A
s
‾
B
s
‾
S
s
V=A_{s}B_{s}\overline{S_{s}}+\overline{A_{s}}\overline{B_{s}}S_{s}
V=AsBsSs+AsBsSs
若 V=0,表示无溢出;若 V=1,表示有溢出
- 采用一位符号位根据数值位的进位情况判断溢出
若符号位(最高位)的进位
C
n
C_n
Cn 与最高数位(此高位)的进位
C
n
−
1
C_{n-1}
Cn−1 相同,说明无溢出,否则,说明有溢出。溢出逻辑表达式为:
V
=
C
n
⊕
C
n
−
1
V=C_{n}\oplus C_{n-1}
V=Cn⊕Cn−1 若 V=0,表示无溢出;V=1,表示有溢出
单符号位补码又称:模2补码;双符号位补码又称:模4补码,双符号位补码在实际存储时只存储1个符号位,运算时会复制1个符号位
- 采用双符号位
运算结果的两个符号位
S
s
1
S
s
2
S_{s1}S_{s2}
Ss1Ss2 相同,表示未溢出;运算结果的两个符号位
S
s
1
S
s
2
S_{s1}S_{s2}
Ss1Ss2 不同,表示溢出,此时最高位代表真正的符号,此高位代表计算结果的符号。溢出逻辑表达式为:
V
=
S
s
1
⊕
S
s
2
V=S_{s1}\oplus S_{s2}
V=Ss1⊕Ss2
若 V=0,表示无溢出;V=1,表示有溢出,
S
s
1
S
s
2
=
01
S_{s1}S_{s2}=01
Ss1Ss2=01 表示结果正溢出,
S
s
1
S
s
2
=
10
S_{s1}S_{s2}=10
Ss1Ss2=10 表示结果负溢出
加减法运算电路
- 运算器本身无法识别所处理的二进制串是有符号数还是无符号数
- 电路的输入,如果是对有符号数进行加减法,则输入的是数对应的补码表示,如果是对无符号数进行加减法,则电路输入的是数对应的二进制表示
- 不论是补码减法还是无符号数减法,都是用被减数加上减数的负数的补码来实现的
- 输入的低位进位信息 Sub(控制是加法还是减法转化的加法):当 Sub=1 时,做减法实现 [ x ] 补 + [ − y ] 补 [x]_补+[-y]_补 [x]补+[−y]补, 当 Sub=0 时,做加法,实现 [ x ] 补 + [ y ] 补 [x]_补+[y]_补 [x]补+[y]补
可通过标识信息区分有符号整数运算结果和无符号整数运算结果

- 加减运算中的指标
- CF=1 表示结果发生溢出,表示有进位、借位
- CF 的结果是由最高位进位
异或Sub 位的结果得到 - 对 xx 没有意义是说该指标不能判断该计算结果是否溢出
有符号数大小的比较
对于有符号数的运算,零标志 ZF、溢出标志 OF、符号标志 SF 才有意义。
假设两个有符号数为A和B:
1)当ZF=1时,说明A=B;
2)当 OF=SF=0 且 ZF=0时,说明 A>B;
3)当 OF≠SF,且 ZF=0 时,说明 A<B `
无符号数大小的比较
对于无符号数的运算,零标志 ZF、进/借位标志 CF 才有意义。
假设两个无符号数 A 和 B:
1)当 ZF=1,说明 A=B
2)当 ZF=0 且 CF=0 时,说明 A>B
3)当 CF=1 时,说明 A<B `
无符号数(补码)的加减法
- 无符号数(补码)的加法:从最低位开始,按位相加(符号位参与运算),并往更高位进位
- 无符号数(补码)的减法:①“被减数”不变,“减数“全部位按位取反、末位+1,减法变加法;②从最低位开始,按位相加,并向更高位进位
无符号数加法/减法的溢出判断
- 手算判断溢出的方法:nbit 无符号整数表示范围 0 ~ 2 n − 1 0~2^n-1 0~2n−1,超出此范围则溢出
- 计算机判断溢出的方法:①无符号数加法的溢出判断:最高位产生的进位=1 时,发生溢出,否则未溢出;②无符号数减法的溢出判断:减法变加法,最高位产生的进位=0 时,发生溢出,否则未溢出
定点数的乘除运算
定点数的乘法
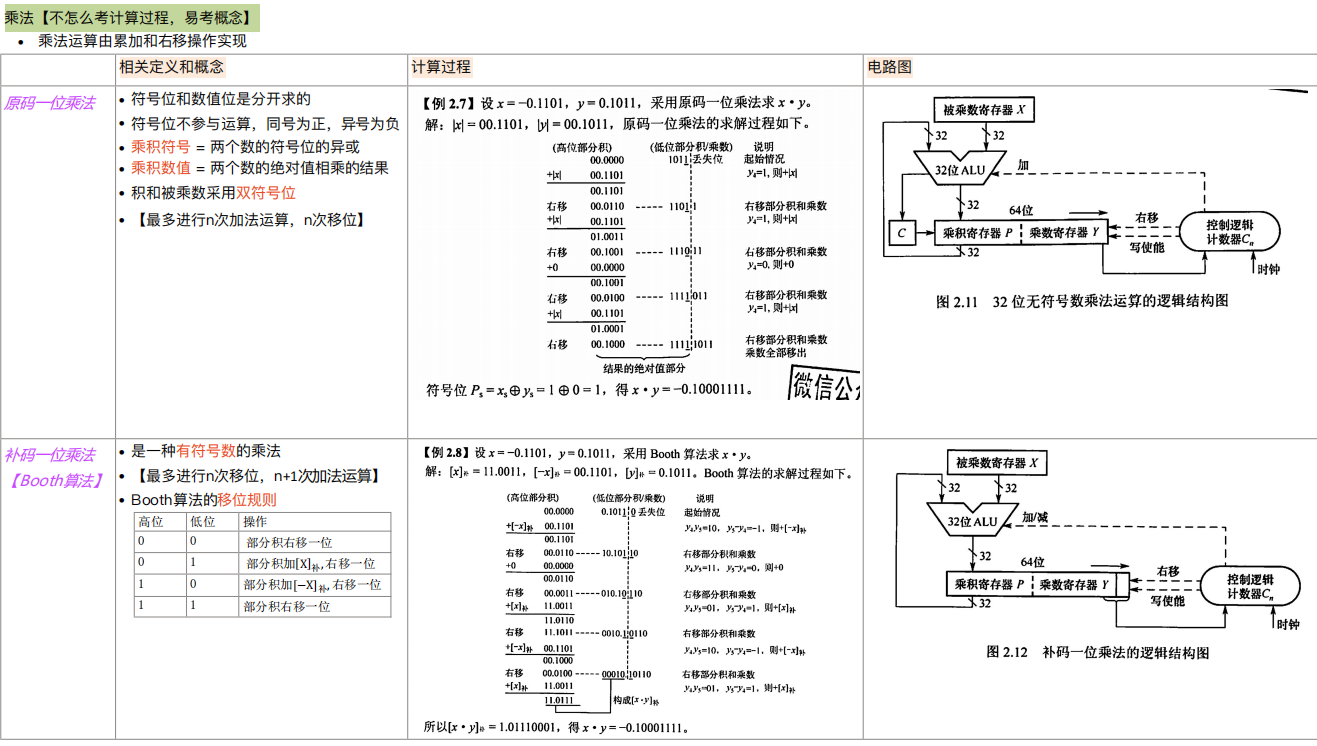
- 原码乘法的特点是符号位与数值位是分开求的
- 原码乘法运算分为两步:①乘积的符号位由两个乘数的符号位“异或”得到;②乘积的数值位是两个乘数的绝对值之积
- 两个定点数的数值部分之积可视为两个无符号数的乘积
- 乘法运算可用加法和移位运算来实现(乘以 2 − 1 2^{-1} 2−1 相当于做一次右移),两个 n 位无符号数相乘共需进行 n 次加法和 n 次移位运算
- 由于参与运算的是两个数的数值位,因此运算过程中的右移操作均为逻辑右移
原码乘法运算的过程归纳:
- 被乘数和乘数均取绝对值参加运算,视为无符号数,符号位为 x s ⊕ y s x_s\oplus y_s xs⊕ys
- 部分积 P i P_i Pi 是乘法运算的中间结果,初值 P 0 = 0 P_0=0 P0=0。从乘数的最低位 y n y_n yn 开始,将前面所得的部分积 P i P_i Pi 加上 X ∗ y n − i X * y_{n-i} X∗yn−i,然后右移移位,此步骤重复 n 次
| 加 | 减 | 乘 | 除 | |
|---|---|---|---|---|
| ACC 累加器, 用于存放操作数或运算结果y | 被加数、和 | 被减数、差 | 乘积高位 | 被除数、余数 |
| MQ 乘商寄存器,在乘、除运算时,用于存放操作数或运算结果 | 乘数、乘积低位 | 商 | ||
| X 通用的操作数寄存器,用于存放操作数 | 加数 | 减数 | 被乘数 | 除数 |
小 Tips
- 乘数的符号位不参与运算,可以省略
- 原码一位乘可以只用单符号位
- 答题时最终结果最好写为原码机器数
原码一位乘法:(机器字长 n+1,数值部分占 n 位)
符号位通过异或确定;数值部分通过被乘数和乘数绝对值的 n 轮加法、移位完成,根据当前乘数中参与运算的位确定(ACC)加什么。若当前运算符=1,则 ( A C C ) + [ ∣ x ∣ ] 原 (ACC)+[|x|]_原 (ACC)+[∣x∣]原;若=0,则(ACC)+0。
每轮加法后 ACC、MQ 的内容统一逻辑右移。
补码乘法运算
- 补码一位乘法(Booth 算法)
- 符号位、数值位都是由被乘数和乘数进行 n 轮加法、移位,最后再多来一次加法
- 每次加法可能+0, + [ x ] 补 +[x]_补 +[x]补、 + [ − x ] 补 +[-x]_补 +[−x]补
- 每次移位是“补码的算数右移”
- 乘数的符号位参与运算
辅助位-MQ 中“最低位”=1 时,(ACC)+ [ x ] 补 [x]_补 [x]补
辅助位-MQ 中“最低位”=0 时,(ACC)+0
辅助位-MQ 中“最低位”=-1 时,(ACC)+ [ − x ] 补 [-x]_补 [−x]补
原码乘法与补码乘法的区别

定点数的除法

#todo待补充
小节选择题答案
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 答案 | B | D | C | B | D | C | C | C | A | A | B | |
| 序号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 答案 | B | B | C | B | A | B | C | B | D | A | C | A |
| 序号 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | ||||
| 答案 | B | |||||||||||
| 25 题后为真题 |
错题序号汇总:5、11、14、20、21,25-29、31-32
22-24 题,听完前面的讲解后会做且作对了。方法一致,以 23 题为例

乘 2,变大,相当于左移 1 位,除以 2,变小,相当于右移 1 位

错题解析
- ALU 作为运算器的核心部件,其属于:组合逻辑电路
- 时间逻辑电路:时间有关,过去输入数据延迟,不利于去做运算器
- 组合逻辑电路:她是看当前输入情况,适用于运算器
- 控制器:指挥各个部件的工作,不做运算器
- ALU 是与寄存器相连的,ALU 不存储运算结果和一些中间变量
- 运算器的部件包括:算术逻辑单元(ALU)、移位器(运算移位操作)、状态寄存器 PSW(判断有无溢出)、通用寄存器组(存储运算结果和中间变量)、数据总线(数据传输)
- 错误选项(非运算器部件):地址寄存器(MAR),用来保存当前 CPU 所要访问的内存单元或 I/O 地址,它是存储器,不属于运算器
-
补码定点整数,符号位为 0,正数,左移时,低位补 0 即可,是正数,原码、反码、补码一样。符号位为 1,负数,左移时,低位补 0,右移时,高位补 1
-
已知补码整数存放于 8 位寄存器,判断算术左移后会不会发生溢出?–D
判断方法
移位运算:左移:正数–>负数,负数–>正数,发生溢出(移位前后值符号改变)
算术运算:①正数+正数=负数,负数+负数=正数,发生溢出;②最高位和此高位进位是否相同,不同则溢出;③双符号位,最高位和此高位不同,发生溢出 溢出:最高位(符号位)进位与最高位数值位不同,溢出 14 题
- 关于 01 和 10,两个位置不同溢出,0 表示正,所以 01 为正溢出,只有正正才会发生正溢出;1 表示负,所以 10 表示负溢出,负负发生负溢出
-
两个 16 进制的机器数相加,可以直接按照正常十进制数的加法相加,只是是满 16 进一,然后将大于 9 的数用 A-F 的字母表示,例如:7E5H+4D3H=CB8H
-
给了两个分别用 8 位补码表示的整数,r1 和 r2 ,要将这两个数的加减乘除结果存储在一个 8 位寄存器中,判断是否会发生溢出?—C
方法: -
老实算,加减 ok,乘除不 ok
-
将补码转换为原码,写出真值,然后 8 位补码可表示范围为(-127,128),加减乘除分别用真值计算,看计算结果是否落在可表示范围。补码转原码一个简单方法是:符号位不动,从右往左找到第一个 1,1 之前的数值位全部取反。由原码得真值,只需要计算符号位之后数值位的和即可
-
模 4 补码和模 2 补码的区别:
- 模 4 补码就是双符号位,模 2 补码就是单符号位
- 模 4 补码更容易检出加减法运算中的溢出问题
- 每个模 4 补码存储时只需一个符号位
- 模 4 补码只有在运算时需要两个符号位
- 模 4 补码,在算术和逻辑单元中一定会做的事情是判断有无溢出,故会需要两个符号位
-
原码乘法:(难点)

-
有关移位运算:—D
- 补码正数左移、右移补 0,负数左移,低位补 0,右移高位补 1,若左移前后的符号位不同,发生溢出
- 无符号数进行逻辑左移时,若该数为正数,左移移了“1”,相当于原码“1”移走了,发生溢出(书面语:若最高位移出的是 1,发生溢出)
- 逻辑移位:操作数看成无符号数,看成正数,左移低位补 0;算术左移:正数,左移、右移都是低位补 0;负数的话,原码,左移也是低位补 0,不过符号位是不动的,比如 1001,左移后为 1010,移走的为第一个 0;补码,左移时,低位补 0,右移时,高位补 1;反码,左移右移都补 1(符号位不变)
- 补码减法,转换为补码的加法,减数全部位取反,末位+1,但是输入加法器时,输入全部位取反后的减数即可,而不是全部位取反,末位+1 的减数 —B
- 输入的低位进位信息 Sub(控制是加法还是减法转化的加法):当 Sub=1 时,做减法实现 [ x ] 补 + [ − y ] 补 [x]_补+[-y]_补 [x]补+[−y]补, 当 Sub=0 时,做加法,实现 [ x ] 补 + [ y ] 补 [x]_补+[y]_补 [x]补+[y]补
- D 选项的减数为全部位取反,末位+1 后的结果
-
#todo暂未理解

-
B
- 方法同 11 题,算出真值 (不计算符号位),进行计算
- r1=-2,r2=-14,r3=-112,r4=-8
- A
- 2x 相当于把 x 整体左移 1 位,y/2 相当于把 y 算术右移 1 位
- 要求是机器数,不转真值,直接相加,逢二进一,还要注意计算结果最高位与此高位符号是否一致,一致未溢出,不一致,溢出
- C
- 给的是真值,问加减乘除那种运算结果会导致溢出,直接计算即可,看计算结果是否在合法范围内
- 8 位定点补码范围(-128,127)
- C
- int 型是 32 位,short 型是 16 位,double64 位
- 机器数一般用补码表示
- 给了 x 和 y 的 int 类型的机器数,问 x 、y 的真值分别是多少,x-y 的机器数是多少
-
A

-
B
浮点数的表示与运算
#文字内容可不看 , #直接看图片总结
浮点数
- 移码只能用于表示整数
- 移码的定义:移码=真值+偏置值

📕规格化浮点数的特点:
- 用原码表示的尾数进行规格化
正数为 0.1xx… xx 的形式,其最大值表示为 0.11… 1;最小值表示为 0.10… 0。尾数的表示范围为: 1 / 2 ≤ M ≤ ( 1 − 2 − n ) 1/2≤M≤(1-2^{-n}) 1/2≤M≤(1−2−n) 规格化的原码尾数,最高数值位一定是 1。负数为 1.1xx… xx 的形式,其最大值表示为 1.10… 0;最小值表示为 1.11… 1。尾数表示范围为 − ( 1 − 2 − n ≤ M ≤ − 1 / 2 ) -(1-2^{-n}≤M≤-1/2) −(1−2−n≤M≤−1/2) - 用补码表示的尾数进行规格化
- 正数为 0.1xx… xx 的形式,其最大值表示为 0.11… 1;最小值表示为 0.10… 0。尾数的表示范围为 1 / 2 ≤ M ≤ ( 1 − 2 − n ) 1/2≤M≤(1-2^{-n}) 1/2≤M≤(1−2−n) 规格化的补码尾数,符号位与最高数值位一定相反。负数为 1.0xx… xx 的形式,其最大值表示为 1.01… 1,最小值表示为 1.00… 0,尾数的表示范围为 − 1 ≤ M ≤ − ( 1 / 2 + 2 − n ) -1≤M≤-(1/2+2^{-n}) −1≤M≤−(1/2+2−n)
- 这里的负数可以用-1/32 和-1 进行理解,小数点后面 1 越多,绝对值越小,加上负号后,绝对值越小的数反而越大。也可以记:真值越大,补码尾数越大,真值越小,补码尾数越小
- 若浮点数用补码表示,数符与尾数小数点后第 1 位数字相异为规格化数
- 基数不同,浮点数的规格化形式也不同。当浮点数尾数的基数为 2 时,原码规格化数的尾数最高位一定是 1。当基数为 4 时,原码规格化数的尾数最高两位不全为 0
- 补码负数算术左移,低位补 0;补码负数算术右移,高位补 1
举例:
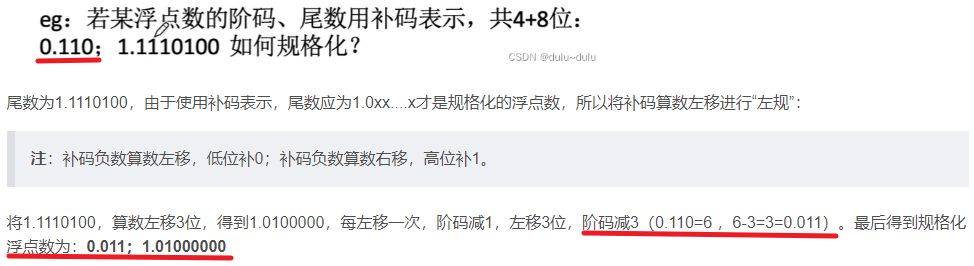
6. 对于规格化之后的尾数,所能表示的最小的数为 0.1,记 1/2. 如果此时阶码为 3 位,并且用补码表示,3 位的补码整数所能表示的最小的数为-4(
−
2
n
−
1
-2^{n-1}
−2n−1),所以对于阶码为 3 的浮点数,其能表示的最小正数为 1.00;0.1=0.00001,如果想要表示的数小于 0.00001,那么就会发生“正下溢”,“负下溢”的原理相同。当出现这两种情况,都通常会将这个数当作机器数 0 处理。
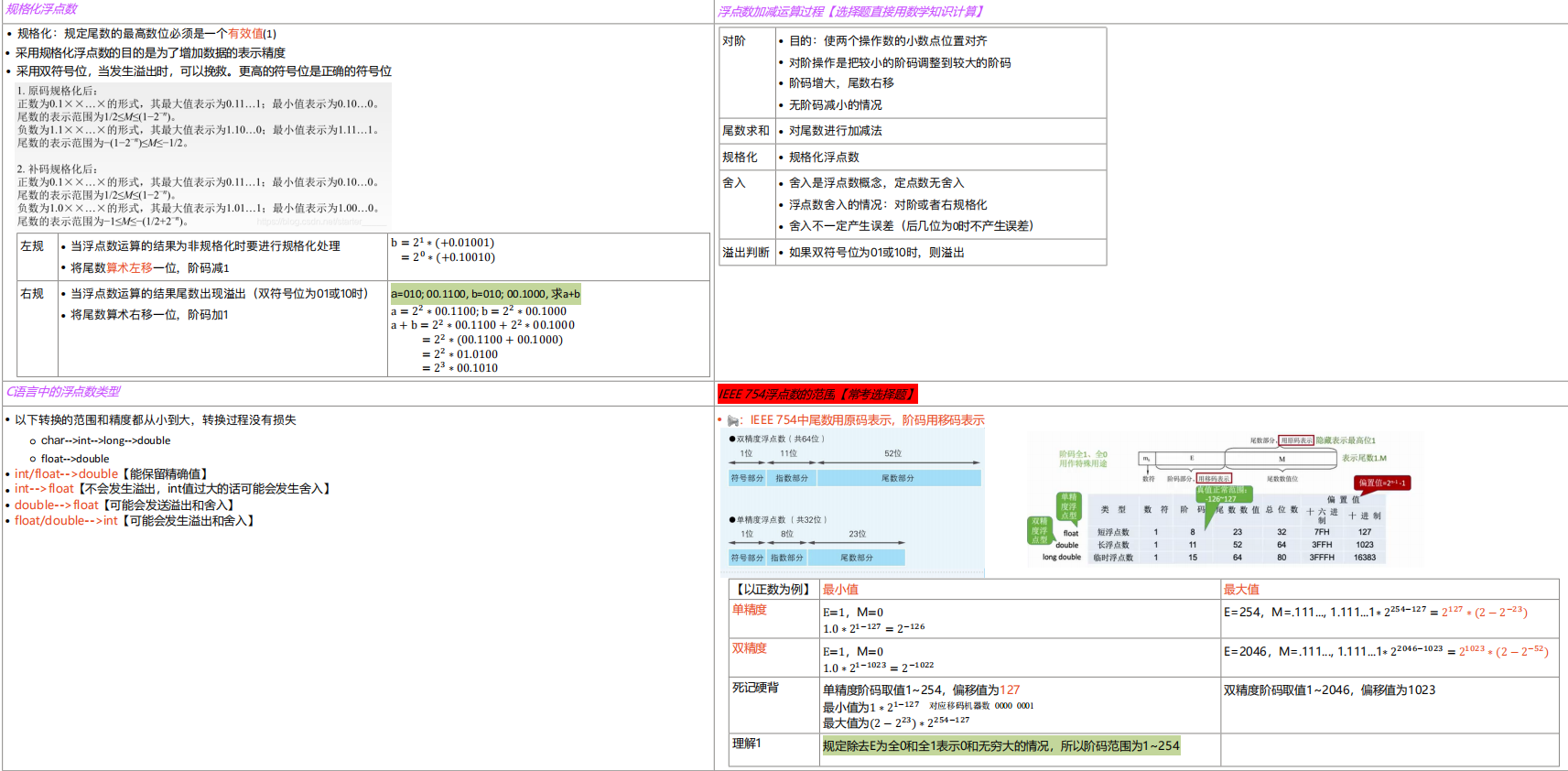
- IEEE 754 规定隐藏位 1 的位置在小数点之前
- 单精度与双精度浮点数都采用隐藏尾数最高位的方法,因而使浮点数的精度更高
- 关于舍入:①若规定只能保留 6 位有效尾数(从最左至右数 6 个数字),多余的直接砍掉;②若砍掉部分非 0,则入 1;③也可以采用四舍五入的原则,当舍弃位≥5 时,高位入 1 可以采用不同的舍入规则
- 偏置值: 2 n − 1 − 1 2^{n-1}-1 2n−1−1,单精度和双精度浮点数的偏置值分别为 127 和 1023。在存储浮点数阶码之前,偏置值要先加到阶码真值上
- 关于溢出:在定点运算中,当运算结果超出数的表示范围时,发生溢出;在浮点运算中,运算结果超出尾数表示范围却不一定溢出(尾数溢出未必导致整体溢出),只有规格化后阶码超出所能表示的范围时,才发生溢出。
溢出相关举例:
例:已知十进制数 X=-5/256,Y=+59/1024,按机器补码浮点运算规则计算 X-Y,结果用二进制表示,浮点数格式如下:阶符取 2 位,阶码取 3 位,数符取 2 位,尾数取 9 位
首先用补码表示阶码和尾数
将这两个数用二进制表示:
再分别转变为补码:
尾数-0.101,阶码 2 − 101 2^{-101} 2−101
对于 2 − 101 2^{-101} 2−101,-101 的补码为 1011,双符号补码为 1101
对于尾数-0.101,补码为 1.011,尾数的数符需要取两位,所以双符号补码为 11.011,由于尾数取 9 位,所以需要进行拓展,得 11.011000000
对于 Y 同理:
①对阶
需要小阶向大阶对齐,计算机是怎么判断谁的结果更小的呢?只需要进行相减的操作,也就是 [ X ] 补 − [ Y ] 补 = [ X ] 补 + [ − Y ] 补 [X]_补-[Y]_补=[X]_补+[-Y]_补 [X]补−[Y]补=[X]补+[−Y]补, [ Y ] 补 − − > [ − Y ] 补 = 00100 [Y]_补-->[-Y]_补=00100 [Y]补−−>[−Y]补=00100 ;11111 (补码)中的前 2 位为双符号位,即 11,1111(补码)–>11,001(原码)=-1
由于 X 的阶数更小,比 Y 的阶数小 1 位,所以需要让 X 的尾数向右移一位 (注意:尾数是负数补码,右移补 1,正数补码,右移补 0),尾数每向右移一位,X 的阶码+1
阶码为 11100,即 11,100, 2 − 100 = 2 − 4 2^{-100}=2^{-4} 2−100=2−4
尾数为 11.1011(补码)—>11.0101 (原码)—>0.0101
注意:这一步进行了右规操作,所以可能需要舍入
②尾数加减
由于双符号位数值不同,说明发生溢出:(01 负溢出,10 正溢出)
为什么呢?结合之前计算的 X,将 X-Y,可以得到尾数的值大于 1 了,由于定点小数没办法表示大于 1 的数,所以溢出了
③规格化:之前讲过,可以通过“右规”的方式,挽救溢出;算术右移,高位补 1/0,具体看符号位是什么,末位的 1 位会被抛弃。别忘了尾数右移,阶码+1,最后得到:
手算的话,相当于进行了下面一步:阶码由-4 变为-3
④舍入:刚刚抛弃了最后 1 位 0,对精度没有影响,所以不需要舍入
⑤判溢出:没有溢出,真值位 2 − 3 ∗ ( − 0.1001111 ) 2 2^{-3}*(-0.1001111)_2 2−3∗(−0.1001111)2
📕若某浮点数需要舍入,通常可以使用以下两种方法:
-
“0 舍 1 入法”
类似于十进制运算中的“四舍五入”,即在尾数右移时,被移去的最高数值位为 0,则舍去;被移去的最高数值位为 1,则在尾数的末位+1。【注🧨】这样做可能会使尾数又溢出,此时需要再做一次右规 -
“恒置 1 法”
尾数右移时,不论丢掉的最高数值位是“1”还是“0”. 都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能

例 1. 将十进制数-0.75 转换为 IEEE 754 的单精度浮点数格式表示
①首先确定单精度浮点数包括 1 位数符,8 位移码,23 位尾数
②将十进制数转化为规格化的二进制数
(
−
0.75
)
10
=
(
−
0.11
)
2
=
(
−
1.1
)
2
∗
2
−
1
(-0.75)_{10}=(-0.11)_2=(-1.1)_2*2^{-1}
(−0.75)10=(−0.11)2=(−1.1)2∗2−1
③从规格化二进制数中可以看到以下信息,单精度浮点型偏移量为 127D,阶码用移码表示,所以需要将阶码真值转换为移码,移码-阶码真值+127=-1+127=126=0111 1110(凑足 8 位)

④按数符,移码,尾数的顺序写出单精度浮点数

例 2. IEEE 754 的单精度浮点数 C0 A0 00 00 H 的值为多少
①将 16 进制数转换为与之对应的二进制数

②从二进制数中可以得到信息

③单精度浮点数的偏移量是 127D,所以阶码真值=移码-偏移量=129-127=
(
2
)
10
(2)_{10}
(2)10
④所以浮点数的真值:

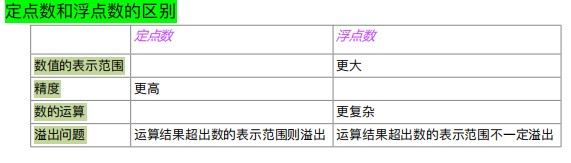
定点数与浮点数的区别
数据的大小端和对齐存储

- 数据按边界对齐方式存放要求其存储地址是自身大小的整数倍
- 半字地址一定是 2 的整数倍,字地址一定是 4 的整数倍,好处是:无论所取的数据是字节、半字还是字,均可一次访存取出
- 当数据不按边界对齐方式存储时,半字长或字长的数据可能在两个存储字中,此时需要两次访存,并对高低字节的位置进行调整后才能得到所需数据,从而影响系统的效率
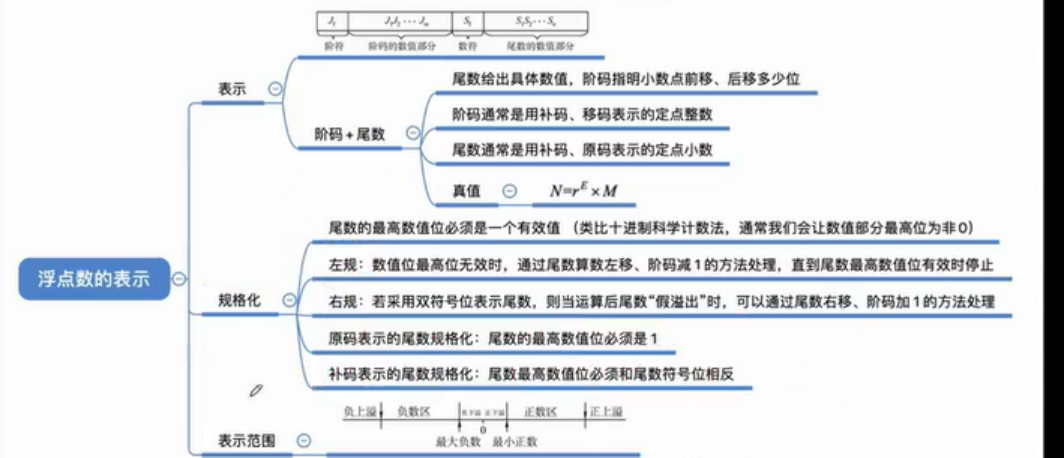
~~### 浮点数的表示
浮点数表示法是指以适当的形式将比例因子表示在数据中,让小数点的位置根据需要而浮动。作用:在位数有限的情况下,既扩大了数的表示范围,又保持了数的有效精度
📕浮点数的表示格式
N
=
(
−
1
)
S
∗
M
∗
R
E
N=(-1)^S*M*R^E
N=(−1)S∗M∗RE
~~- S 取值 0 或 1,用来决定浮点数的符号;
M 是一个二进制定点小数,称为尾数,一般用定点原码小数表示;尾数的位数反映浮点数的精度E 是一个二进制定点整数,称为阶码或指数,用移码表示;阶码的位数反映浮点数的表示范围,阶码的值反映浮点数的小数点的实际位置,阶码指明了小数点要向前/向后移动记为R 是基础 (隐含),可以约定为 2、4、16 等浮点数由符号、尾数和阶码三部分组成,阶码反映数值大小,尾数反映精度
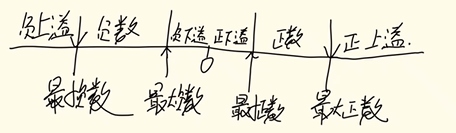
📕浮点数的表示范围
- 原码是关于原点对称的,故浮点数的范围也是关于原点对称的,如图:

~~- 运算结果大于最大正数时称为正上溢,小于绝对值最大负数时称为负上溢,正上溢和负上溢统称上溢
数据一旦产生上溢,计算机必须中断运算操作,进行溢出处理当运算结果在 0 至最小正数之间称为正下溢,在 0 至绝对值最小负数之间称为负下溢,正下溢和负下溢统称下溢数据下溢时,浮点数值趋于零,计算机将其当作机器零处理
~~📕浮点数的规则化·
为了在浮点数运算过程中尽可能多的保留有效数字的位数,使有效数字尽量占满尾数数位,必须在运算过程中对浮点数进行规格化操作规格化:是指通过调整一个非规格化浮点数的尾数 M 和阶码 E 的大小,使非零浮点数在尾数的最高数位上保证是一个有效值
小节选择题答案
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 答案 | C | B | C | C | D | C | A | A | D | B | A | D | A | ||
| 序号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 答案 | C | A | D | D | C | D | |||||||||
| 序号 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
| 答案 | C | D | |||||||||||||
| 序号 | 46 | 47 | 48 | 49 | 50 | ||||||||||
| 答案 |
34 题后为往年真题
错题序号汇总:3、5、6、9、11、12、13、16-18、20、23、24、27-36、38-50
错题解析
- B
- 长度相同,格式相同的两种浮点数,基数不同,基数大的数可表示的数的范围大但精度低
- C
- 变形补码,其实就是双符号位,不管如何加减,只要数值位超过便会溢出。
- 定点数和浮点数都可能溢出
- 规格化浮点运算中,若某浮点数为
2
5
∗
1.10101
2^5*1.10101
25∗1.10101,其中尾数为补码表示,则该数:—C 左移一位规格化为
1.01010
∗
2
4
1.01010*2^4
1.01010∗24
浮点数规格化
- 对原码尾数,最高数值位一定为 1,原码正数 0.1xxx,最大值 0.111… 111= 1 − 2 − n 1-2^{-n} 1−2−n,最小值 0.1000… 000=0.5;原码负数 1.1xxxx,最大值 1.1000… 000=-0.5,最小 1.1111…= − ( 1 − 2 − n ) -(1-2^{-n}) −(1−2−n)
- 对补码尾数,补码正数 0.111…= 1 − 2 − n 1-2^{-n} 1−2−n,最小 0.1000…=0.5,补码负数 1.0xxx,最大值 1.0111… 111= 1 − 2 − n 1-2^{-n} 1−2−n,最小值 1.0000… 000=-1
-
B (同 5)
-
对阶操作时,一定是阶数小的向阶数大的靠齐,阶码一定增大,尾数部分进行算术右移
-
浮点数的 IEEE 754 标准对尾数编码采用的是原码,阶码编码采用的是移码
-
在 IEEE 754 标准规定的 64 位浮点数格式中,符号位为 1 位,阶码为 11 位,尾数为 52 位,则它所能表示的最小规格化负数为?----B
- 11 位阶码,可表示的移码范围: − 2 10 至 2 10 − 1 = − 1024 至 1023 -2^{10} 至 2^{10}-1=-1024 至1023 −210至210−1=−1024至1023
- 尾数部分:要想得到规格化下最小负数,得使尾数绝对值下数值最大,1.1111111…= 1 − 2 − 52 1-2^{-52} 1−2−52 —>绝对值,算上隐含的 1,结果为 2 − 2 − 52 2-2^{-52} 2−2−52,又是负数,即为: − ( 2 − 2 − 52 ) -(2-2^{-52}) −(2−2−52)
- 最终结果为 − ( 2 − 2 − 52 ) ∗ 2 1023 -(2-2^{-52})*2^{1023} −(2−2−52)∗21023
- D
- 在浮点数编码表示中,基数在机器数中不出现,是隐含的
- D

- 移码转补码,符号位取反,其他照抄

- D
- 规格化浮点数的目的是为了提高精度
- 浮点数可以增加数据的表示范围
- D
- 若计算机字长无限,无论如何加减都可以存储下来,在计算机中,表示的数有时会发生溢出,根本原因是计算机的字长有限
- 正数的原反补码一致
- 规格化后的浮点数,正数原码一定为 0.1xxx… xxx,两个浮点数阶码不一致,其他都一致,阶码大的浮点数大
-
在浮点运算中,下溢指的是运算结果的绝对值小于机器所能表示的最小绝对值
-
判断浮点数运算是否溢出,取决于阶码是否发生上溢(对阶时,阶码是否超过阶码所能表示的最大数)尾数溢出可以通过左规或右规进行规格化
-
B
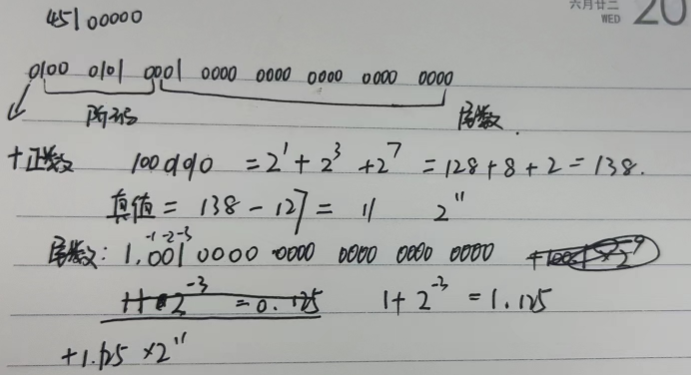
-
A

- x=-126=-1111110B=-1.111110B* 2 6 2^6 26
- y=15.75=1111.11B=1.11111* 2 3 2^3 23
- x 的阶数为 6,y 的阶数为 3,对阶一般是小阶向高阶看齐,所以 y 的阶数 3–>6,让 y 尾数右移 3 位,变成 0.0011111B* 2 6 2^6 26
- 阶码真值 6,阶码是用移码表示,移码=真值+偏置值=6+127=133
- A 选项移码 010000101=133,B 选项移码 010000110=134
- A
- 在 IEEE 754 标准浮点数格式中,非规格化浮点数表示为:阶码为 0,尾数为任意非 0 的二进制数
- 非规格化浮点数,阶码一定为 0,且全是 0,它用来表示 0 以及非常接近 0 的数,偏置值为 126,移码全为 0 表示-126, 0. M ∗ 2 − 126 0.M*2^{-126} 0.M∗2−126, 尾数 M任意
- 在规格化的浮点数中,将阶码部分的 n 位移码表示改为 n 位补码表示,其他不变,则浮点数的表示范围不变,表示形式有变化
- 位数相同,补码与移码表示范围相同
- 8bit 时,补码表示范围-128127,移码表示范围-126127(全 0 和全 1 有其他用途)
- 阶码全 0,尾数不全为 0,表示非规格化数,且偏置值为 126
- 当阶码全 0,尾数全 0—>真值±0
- 当阶码全 1,尾数全 0—>真值±∞
- 当阶码全 1,尾数不全为 0,表示非数值“NAN”
- D

- 达到最大,首先得是①正数,②阶码正,数大;③尾数正,数大
- 尾数 8 位,有 1 个符号位正 0,其他取 1—>0.1111111—> 1 − 2 − 7 1-2^{-7} 1−2−7
- 阶码 4 位,符号正,0111—>7
- 最大正数为 1 − 2 − 7 ∗ 2 7 1-2^{-7}*2^7 1−2−7∗27 = 2 7 − 1 2^7-1 27−1
- D
- 补码规格化,符号位与最高数值位不同
- C

- 基数 2–>原码小数点,后 1 位一定为 1,不为 0
- 基数 4–>原码小数点,后 2 位一定不为 0
- 不管基数为多少,小数点后(基数/2)位真值一定大于 1
- 关于舍入的说法:
- 只有浮点数才有舍入,定点数无舍入概念,舍入方法:①0 舍 1 入,②恒置 1 法
- 浮点数舍入只有两种情况才会有舍入:①对阶,②右规格化
- 舍入不一定产生误差
-
D
边界对齐:有多大字节就要放在含有相同字节大小的位置,不可随意放;信息单元的存储地址是其字节长度的整数倍
边界不对齐:可随意组合,只要能存入就可 -
D

- I,dx+dy–>先将 int 类型 x,y—>double 类型,再将两个数相加。int–>double 不会溢出也不会有精度损失,但 (double)(x+y) 是先将 int 类型相加得到一个值,然后将这个值转换为 double 类型存储,会比真实值要小,False
- II,dx 乘 dx >=0,因为 double 采用 IEEE754,符号位与数值位分开求。若 x 为负数,负负得正;若 x 为正数,结果≥0,True
- III,dx/dx == dy/dy,非永真,若 x 和 y 其中一个为 0,另一个不为 0,则不相等。False
- Ⅳ,(dx+dy)+dz == dx+(dy+dz),dx,dy,dz 都是 x,y,z 先从 int 类型转为 double 类型,double 类型尾数为 52 位,一定比 23 位多,对阶时,尾数一定不会舍入,True
- A

- 字节编址是说每个地址只存一个字节(1B)—short 意味着每次存放地址加 2B
- 小端存储和大端存储:
- 例如: 01 23 45 67H(数据)7 这一端为数据低位
- 存储地址:01H 02H 03H 04H,01H 端为地址低位,04H 端为地址高位
- 大端存储(方便人类阅读):01H 23H 45H 67H,数据高位放地址的低位
- 小端存储:67H 45H 23H 01H,数据低位放地址的低位

- 找到-6 后,写出补码,因为数据低位要放在地址低位,即 1111 1010 为数据地址,存放的地址低位为 FAH(H15, A10,分别对应 1111,1010)
- D

- 字节编址–>1 个地址–>存 1B–>8bit
- 小端方式:数据低位放地址低位
- int 类型 i–>地址:08000000H–>第 1 个地址,为地址低位
- 1 个数字为 4 个 bit,所以 67 两个数字同时存储
- A

- 边界对齐:信息单元的存储地址是其数据字节长度的整数倍
- char 类型–>1B–>数据字节长度为 1–>它的存储地址为 1 的整数倍
- unsigned–>4B–>数据字节长度为 4–>它的存储地址为 4 的整数倍
- id–>char–>1B–>0x8049820
- post–>4 的整数倍地址,24 开始,放了 4B,一直放到 27
- phone–>1B–>1 的整数倍
- 先存 id,再存 post,最后存 phone,所以只能存 28 开始
- A

- 大端方式,数据高位放地址低位
- int n=0xA1B6–>m=n (把 n 赋值给 m), -->将 int 转为无符号类型 int,其实还是 int,只是有符号数变成无符号数,开始 32 位之后还是 32 位,m 的值还是 A1B6H,即 1010 0001 1011 0110
- m>>1,表示将 m 右移 1 位,<<表四左移,无符号数右移,高位添 0,即 0101 0000 1101 1011 ,移位后 m 为 500BH
- D

- i=12345, f = 1.2345 ∗ 2 3 = 1234.5 f=1.2345*2^3=1234.5 f=1.2345∗23=1234.5
- A :先将 int i=12345 转为 double 类型(1 11 52+1)可以完全装下,范围增大,且精度没有损失,所以转换为 double 类型后的 i=12345 之后又变为 int 类型,结果不变 i=12345
- B:先将 float f=1234.5 转为 double 类型,可以安全装下,float 是 1+8+(23+1),double 是 1+11+(52+1), double f=1234.5 再转为 float 类型,结果不变 f=1234.5
- C:int i=12345–>float 类型,完全可以放下 12345,float i=12345,同理 A
- D:float f=1234.5 (有小数)–>转为 int(int 类型不可表示小数,会直接将小数部分舍去)int f=1234,再转为 f 类型依然是 1234
- B

- m int 类型=13,a float 类型=12.6,x 是 float 类型
- 在进行数据运算时,若未表明强制类型转换,默认整数与整数运算结果为整数,实数与整数运算结果为实数
- x=m/2+a/2
- m/2 = 13/2=6 (取整),a/2=12.6/2=6.3,x=6+6.3=12.3,最后一行打印%f 表示可以输出小数,即保留小数点后 6 位则 12.3=12.300000
以下为真题
- D

- 此题未说在 IEEE 754 下,所以尾数没有隐含位 1,所以普通浮点数只用保证最高数值位小数点后一位为 1 即可,阶码为 5,尾数为 7(有 2 个符号位)
- x = 2 7 ∗ 29 / 32 x=2^7*29/32 x=27∗29/32 -->阶码真值为 7(补码),所以 x=00111 为阶码,00 为符号位,29=16+8+4+1=0011101,然后 29/32 相等于 29 ∗ 2 − 5 = 0011101 ∗ 2 − 5 = 00.11101 29*2^{-5} =0011101*2^{-5}=00.11101 29∗2−5=0011101∗2−5=00.11101,
- y = 2 5 ∗ 5 / 8 y=2^5*5/8 y=25∗5/8 -->阶码真值为 5(补码),所以 y=00101 为阶码,00 为符号位,5=000101,然后 5/8 相当于 2 5 ∗ 5 ∗ 2 − 3 = 000101 ∗ 2 − 3 = 00.101 2^5*5*2^{-3}=000101*2^{-3}=00.101 25∗5∗2−3=000101∗2−3=00.101
- x=00111; 00.11101 (阶码;尾数),y=00101; 00.10100,x 阶码真值为 7,y 阶码真值为 5,小阶码向大阶码靠齐,y–>x 对齐,y 尾数要右移 2 位为 00.00101,此时阶码相同( 2 7 2^7 27)所以尾数相加即可,相加后发生溢出,需要右规,阶码加 1=00111+1=01000,阶码发生溢出,整体计算结果溢出
- B

- E3 表示乘以 1 0 3 10^3 103,E100 表示乘以 1 0 100 10^{100} 10100
- i int 类型=785,f 为 IEEE 754 单精度 float 类型浮点数=1.5678E3,d 为 IEEE 754 双精度 double 类型浮点数=1.5E100
- I: int i=785–>10 个 bit 肯定可以表示,float: 1 8 23+1 尾数 23 位肯定可以装得下,i 变为 float 再转为 int 型结果不变 True
- II:float f = 1.5678 ∗ 1 0 3 = 1567.8 1.5678*10^3=1567.8 1.5678∗103=1567.8,先转为 int f = 1567 丢失 0.8,再转为 float f 不等于原始 f False
- Ⅲ:float f = 1.5678 ∗ 1 0 3 = 1567.8 1.5678*10^3=1567.8 1.5678∗103=1567.8,先转为 double 类型,尾数 52 装 23 肯定装得下,精度不损失还是 1567.8,再转为 float 类型,结果不变,True
- Ⅳ:d+f,d 和 f 的阶不一致,需要对阶,差距太大,d+f 得到的数不是真实想要的数,结果损坏,不算也罢
- A

- x=-8.25–>转为二进制:-1000.01–> − 1.00001 ∗ 2 3 -1.00001*2^3 −1.00001∗23
- 阶码真值 3,真值=移码-偏置值(无符号数去算,IEEE 下 127),有 3=移码-127—>移码无符号数为 130
- 移码 130 = 1000 0010 ,尾数 1.00001 ∗ 2 3 1.00001*2^3 1.00001∗23
- FR1 内容:1 1000 0010 0000 1000 0000 0000 000—>4 个数一组进行计算
- D
- float 类型(IEEE 754 下)能表示的最大正整数是 2 128 − 2 104 2^{128}-2^{104} 2128−2104
- D

- 小端存储:数据低位放地址低位;边界对齐:信息单元的存储地址是其字节长度的整数倍
- record 结构体,int 占 4B,char 占 1B,short 占 2B 一共占 7B,首地址 0xC008
- record a=273 = 0001 0001 0001 = 0x 0000 0111 (十六进制)–为什么转 16 进制,一个数字占 1B
- 先存 a,4 的整数倍 0XC008 即是,占 4 个位置到 0XC00B,然后放 b,b 占一个,0xC00C,放 c,short 类型占 2B,放 2 的整数倍,得从 0xC00E 开始
- A

- C640 0000H --> 1100 0110 0100 0000 0000 0000 0000
- 阶码(移码):1000 1100 -->看成无符号数计算=128+8+4=140,真值=移码-偏置值=140-127=13 , 2 13 2^{13} 213
- 尾数隐含 1,符号为 1,-1.100 0000 0000 0000 0000
- 该值为 − 1.1000000000000000000 ∗ 2 13 -1.100 0000 0000 0000 0000*2^{13} −1.1000000000000000000∗213
- 十进制表示 − ( 1 + 0.5 ) ∗ 2 13 -(1+0.5)*2^{13} −(1+0.5)∗213
- A

- IEEE 754 float 类型,偏置值 127
- f1=CC90 0000H,f2=B0C0 0000H
- f1=1100 1100 1001 0000 0000 0000 0000 0000 ,符号为 1,阶码 10011001=1+8+16+128,真值=移码-偏置值=1+8+16+128-127=26 , 2 26 2^{26} 226,尾数(隐含 1):1.001 0000 0000 0000 0000 0000,,最终结果: − 1.001 ∗ 2 24 = − 1.125 ∗ 2 24 -1.001*2^{24}=-1.125*2^{24} −1.001∗224=−1.125∗224
- f2=1011 0000 1100 0000 0000 0000 0000 0000,符号为 1,阶码 01100001=1+32+64=97,真值=97-127=-30, 2 − 30 2^{-30} 2−30,尾数 1.10…,最终结果 − 1.1 ∗ 2 − 30 = − 1.5 ∗ 2 − 30 -1.1*2^{-30}=-1.5*2{-30} −1.1∗2−30=−1.5∗2−30
- f1 和 f2 符号相同,f2>f1
- 关于浮点数加减运算的说话正确的是:—D
- 对阶操作不会引起阶码上溢或下溢,但是在不同浮点数类型下进行对阶,可能出现溢出
- 右规和尾数舍入都可能引起阶码上溢
- 左规时可能引起阶码下溢
- 尾数溢出时结果不一定溢出,结果是否溢出主要是看阶码是否发生上溢
- A

- 字节编址:每个地址只存一个字节 1B
- 小端存储:数据低位放地址低位
- double 类型(1 11 52+1),机器数 1122 3344 5566 7788H,存放是从 40 开始,(40) 88H, (41) 77H, (42) 66H ,(43) 55H, (44) 44H, (45), 33H, (46) 22H
- IEEE 754 单精度浮点格式表示的数中,最小的规格化正数是: 1.0 ∗ 2 − 126 1.0*2^{-126} 1.0∗2−126
- 规格化:小数点前一位为 1,最小:阶码最小,8bit–>-126-127, 尾数 ∗ 2 − 126 尾数*2^{-126} 尾数∗2−126, 1 后全取 0 最小,最终结果 1.0 ∗ 2 − 126 1.0*2^{-126} 1.0∗2−126
-
A


-
D

- 字节编址 1B 一个地址、小端、边界对齐
- a 的首地址 2020 FE00H,x2=1234 0000H, 问 34H 所在存储单元地址:
- short 2B2 的整数倍,首地址为 2020 FE00H,先存储 short 类型 x1,存储地址为 2020 FE00H,再存储 int 型 x2,存放在 4 的整数倍地址中,00H 放置 2020 FE04H,00H–>05H,34H–>06H,12H–>07H
- A

- C800 0000H = 1100 1000 0000 0000 0000 0000 0000 0000 ,
- 若 x 为 int 类型,已知补码–>原码:10111 000 0000 0000 0000 0000 0000 0000= − ( 2 29 + 2 28 + 2 27 ) = − 2 27 ( 4 + 2 + 1 ) = − 7 ∗ 2 27 -(2^{29}+2^{28}+2^{27})=-2^{27}(4+2+1)=-7*2^{27} −(229+228+227)=−227(4+2+1)=−7∗227
- 若 x 为 float 类型,符号为 1,排除 CD,阶码= 10010000= 16+128,真值=17, 2 17 2^{17} 217 尾数 (隐含 1):1.000 0000 0000 0000 0000 0000,最终结果 − 1.000... ∗ 2 17 -1.000...*2^{17} −1.000...∗217
- A

- 直接看小数部分即可,A:0.2,B:0.25,C:0.0,D:0.5,0.5,0.25 都可以表示出来 2 − 1 2^{-1} 2−1, 2 − 2 2^{-2} 2−2,0.2 不可
-
A


-
A

-
A

- IEEE 754 下,8020 0000H=1000 0000 0010 0000 0000 0000 0000 0000,符号为 1,阶码全 0,尾数不全为 0,非规格化小数,且偏置值为 126,表示为 ± ( 0. 尾数 ) ∗ 2 − 126 = − 0.01 ∗ 2 − 126 = − 1 ∗ 2 − 128 = − 2 − 128 ±(0. 尾数)*2^{-126}=-0.01*2^{-126}=-1*2^{-128}=-2^{-128} ±(0.尾数)∗2−126=−0.01∗2−126=−1∗2−128=−2−128,








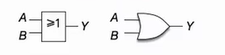
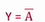
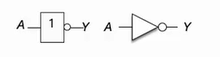

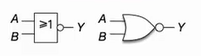
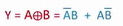
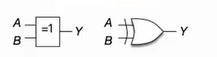
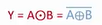
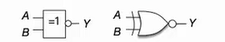

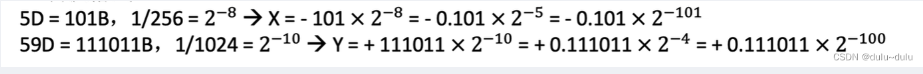

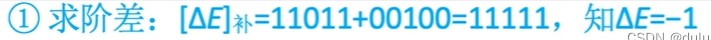


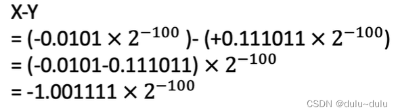

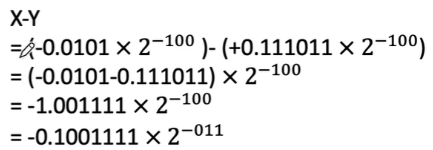














 759
759

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








