【luogu P5320】勘破神机（数学）（数列特征方程）（第一类斯特林数）

勘破神机

题目链接：luogu P5320

题目大意

给你 $l,r,k$（其中 $l,r$ 很大，$k\le 501$），求：
$\frac{1}{r-l+1}\sum _{i=l}^r{C}_{f_i}^k$
$\frac{1}{r-l+1}\sum _{i=l}^r{C}_{g_i}^k$
$f_n$ 为一个 $2\ast n$ 的网格往里面放 $1\ast 2$ 的块填满的方案，$g_n$ 则是一个 $3\ast n$ 的网格。

思路

首先 $2$ 的答案我们可以看出答案其实是贴合与斐波那契数列 $F_i$。
具体看一看会发现是 $f_i=F_{i+1}$，所以记得 $l,r$ 加一。
然后斐波那契嘛，$f_i=f_{i-1}+f_{i-2}$，然后可以表示成那个带根号的通式嘛。

然后我们通过特征方程这个东西，我们知道如果有一个二阶递推式，我们可以把它表示成一个通项公式。
于是开始了下面的步骤：

2

$f_i=f_{i-1}+f_{i-2}$
$f[n]=\frac{\sqrt{5}}{5}[(\frac{1+\sqrt{5}}{2}{)}^n-(\frac{1-\sqrt{5}}{2}{)}^n]$
$A=\frac{\sqrt{5}}{5},\alpha =\frac{1+\sqrt{5}}{2},B=-\frac{\sqrt{5}}{5},\beta =\frac{1-\sqrt{5}}{2}$

3

思考要如何推出 $f$ 的值，首先把 $f_0,f_1$ 求出，因为可以作为边界，而且也是特征方程需要的。

$f_0=1,f_1=3$
$f_i$ 长度为 $2i$ 的答案（所以记得两个边界要改，但是注意 $r-l+1$ 要用之前的值）

于是进行思考，发现可以新放进来一个 $2\ast 3$ 的，然后有 $3$ 中方法。
然后发现只有这样不够，因为可能会出现这样的：

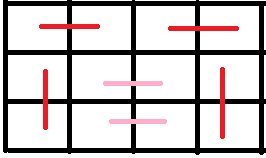
而且呢，中间的粉色可能不止两个：

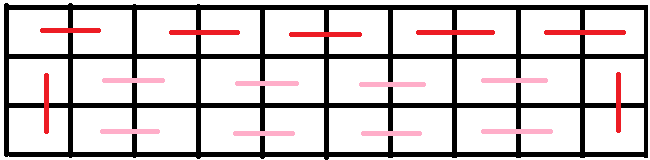
然后粉色可以是在 $1,2$ 行或者 $2,3$ 行，所以我们可以列出这样的式子：

$f_i=3f_{i-1}+2(f_{i-2}+f_{i-3}+...)$
$f_i=3f_{i-1}+2(\sum _{j=0}^{i-2}{f}_j)$
$f_{i-1}=3f_{i-2}+2(\sum _{j=0}^{i-3}{f}_j)$
$f_i-f_{i-1}=3f_{i-1}-f_{i-2}$
$f_i=4f_{i-1}-f_{i-2}$

搞出了二阶递推式，就直接开始求通项公式吧！

$f_i-4f_{i-1}+f_{i-2}=0$
$x^2-4x+1=0$
$x_1=\frac{4+2\sqrt{3}}{2},x_2=\frac{4-2\sqrt{3}}{2}$
$x_1=2+\sqrt{3},x_2=2-\sqrt{3}$
带入 $f_0=1,f_1=3$
$A{x}_1^n+B{x}_2^n=f_n$

$A+B=1$
$A(2+\sqrt{3})+B(2-\sqrt{3})=3$

$A(2+\sqrt{3})+(1-A)(2-\sqrt{3})=3$
$A(2+\sqrt{3})+2-\sqrt{3}-A(2-\sqrt{3})=3$
$2\sqrt{3}A=1+\sqrt{3}$
$A=\frac{1+\sqrt{3}}{2\sqrt{3}}=\frac{\sqrt{3}+3}{6}$
$A=\frac{3+\sqrt{3}}{6},B=\frac{3-\sqrt{3}}{6}$
$f[n]=\frac{3+\sqrt{3}}{6}(\frac{4+2\sqrt{3}}{2}{)}^n+\frac{3-\sqrt{3}}{6}(\frac{4-2\sqrt{3}}{2}{)}^n$
$A=\frac{3+\sqrt{3}}{6},\alpha =\frac{4+2\sqrt{3}}{2},B=\frac{3-\sqrt{3}}{6},\beta =\frac{4-2\sqrt{3}}{2}$
$A=\frac{3+\sqrt{3}}{6},\alpha =2+\sqrt{3},B=\frac{3-\sqrt{3}}{6},\beta =2-\sqrt{3}$

---

于是我们似乎把 $f_i$ 表示成了一个很好的形式，考虑开搞。

$f_i=A{\alpha }^i+B{\beta }^i$
$\sum _{i=0}^n\left(\genfrac{}{}{0ex}{}{f_i}{k}\right)$
$\sum _{i=0}^n\frac{f_i!}{k!(f_i-k)!}$
$\sum _{i=0}^n\frac{f_i^{\underline{k}}}{k!}$
$\frac{1}{k!}\sum _{i=0}^n\sum _{j=1}^k(-1{)}^{k-j}s(k,j)f_i^j$（斯特林数与下降幂的转化）
（补充：$x^{\overline{k}}=\sum _{j=1}^{k}s(k,j)x^j$）
$\frac{1}{k!}\sum _{i=1}^k(-1{)}^{k-i}s(k,i)\sum _{j=0}^n{f}_j^i$

设 $g_{n,j}=\sum _{i=0}^n{f}_i^j$
$f_i=A{\alpha }^i+B{\beta }^i$
$g_{n,j}=\sum _{i=0}^n(A{\alpha }^i+B{\beta }^i{)}^j$
$g_{n,j}=\sum _{k=0}^j\left(\genfrac{}{}{0ex}{}{j}{k}\right)\sum _{i=0}^n(A{\alpha }^i{)}^k(B{\beta }^i{)}^{j-k}$
$g_{n,j}=\sum _{k=0}^j\left(\genfrac{}{}{0ex}{}{j}{k}\right)A^k{B}^{j-k}\sum _{i=0}^n{\alpha }^{ik}{\beta }^{i(j-k)}$
$g_{n,j}=\sum _{k=0}^j\left(\genfrac{}{}{0ex}{}{j}{k}\right)A^k{B}^{j-k}\frac{1-{\alpha }^{(n+1)k}{\beta }^{(n+1)(j-k)}}{1-{\alpha }^k{\beta }^{j-k}}$（等比数列求和）

$\frac{1}{k!}\sum _{i=1}^k(-1{)}^{k-i}s(k,i)\sum _{j=0}^n{f}_j^i$
$\frac{1}{k!}\sum _{i=1}^k(-1{)}^{k-i}s(k,i)g_{n,i}$
$\frac{1}{k!}\sum _{i=1}^k(-1{)}^{k-i}s(k,i)(\sum _{p=0}^i\left(\genfrac{}{}{0ex}{}{i}{p}\right)A^p{B}^{i-p}\frac{1-({\alpha }^p{\beta }^{i-p}{)}^{n+1}}{1-{\alpha }^p{\beta }^{i-p}})$

---

小提示：
记得特判等比数列公比为 $1$。

代码

#include<cstdio>
#define ll long long
#define mo 998244353

using namespace std;

const int K = 550;
int gen;
int T, op, k;
ll C[K][K], S[K][K], l, r;

ll ksm(ll x, ll y) {
	ll re = 1;
	while (y) {
		if (y & 1) re = re * x % mo;
		x = x * x % mo; y >>= 1;
	}
	return re;
}

struct complex {
	ll x, y;
	
	complex(ll a = 0, ll b = 0) {
		x = a; y = b;
	}
}A, B, alpha, beta;//x+sqrt{y}
complex operator +(complex x, complex y) {
	return (complex){(x.x + y.x) % mo, (x.y + y.y) % mo};
}
complex operator -(complex x) {return (complex){(mo - x.x) % mo, (mo - x.y) % mo};}
complex operator -(complex x, complex y) {return x + (-y);}
complex operator *(complex x, complex y) {
	return (complex){(x.x * y.x + gen * x.y * y.y) % mo, (x.x * y.y + x.y * y.x) % mo};
}
complex inv(complex x) {
	ll fm = ksm((((x.x * x.x - gen * x.y * x.y) % mo + mo) % mo) % mo, mo - 2);
	return (complex){x.x * fm % mo, (mo - x.y) * fm % mo};
}

complex ksm(complex x, ll y) {
	complex re = complex(1, 0);
	while (y) {
		if (y & 1) re = re * x;
		x = x * x; y >>= 1;
	}
	return re;
}

void Init() {
	C[0][0] = 1;
	for (int i = 1; i < K; i++) {
		C[i][0] = 1; for (int j = 1; j < K; j++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mo;
	}
	S[0][0] = 1;
	for (int i = 1; i < K; i++) {
		for (int j = 1; j < K; j++)
			S[i][j] = (S[i - 1][j - 1] + (i - 1) * S[i - 1][j] % mo) % mo;
	}
	
	gen = (op == 2) ? 5 : 3;
	if (op == 2) {
		A = (complex){0, ksm(5, mo - 2)}; alpha = (complex){ksm(2, mo - 2), ksm(2, mo - 2)};
		B = (complex){0, (mo - ksm(5, mo - 2)) % mo}; beta = (complex){ksm(2, mo - 2), (mo - ksm(2, mo - 2)) % mo};
	}
	if (op == 3) {
		A = (complex){ksm(2, mo - 2), ksm(6, mo - 2)}; alpha = (complex){2, 1};
		B = (complex){ksm(2, mo - 2), (mo - ksm(6, mo - 2)) % mo}; beta = (complex){2, mo - 1};
	}
}

ll slove(ll n) {
	ll ans = 0, jc = 1; ll di = ((k & 1) ? 1 : mo - 1);
	for (int i = 1; i <= k; i++, di = mo - di) {
		complex sum; jc = jc * i % mo;
		for (int p = 0; p <= i; p++) {
			complex alphabeta = ksm(alpha, p) * ksm(beta, i - p);
			//你是一个一个一个特判啊啊啊！！！
			if (alphabeta.x == 1 && alphabeta.y == 0) {//特判公比为1的情况
				sum = sum + ((complex){C[i][p], 0} * ksm(A, p) * ksm(B, i - p) * (complex){(n + 1) % mo, 0});
				continue;
			}
			sum = sum + ((complex){C[i][p], 0} * ksm(A, p) * ksm(B, i - p) * ((complex){1, 0} - ksm(alphabeta, n + 1)) * inv((complex){1, 0} - alphabeta));
		}
		if (sum.y) {printf("f\n"); return -1;}
		(ans += di * S[k][i] % mo * sum.x % mo) %= mo;
	}
	return ans * ksm(jc, mo - 2) % mo;
}

int main() {
	scanf("%d %d", &T, &op);
	Init();
	while (T--) {
		scanf("%lld %lld %d", &l, &r, &k); ll sz = (r - l + 1) % mo;
		if (op == 2) l++, r++;
			else l = (l + 1) / 2, r = r / 2;
		printf("%lld\n", (slove(r) - slove(l - 1) + mo) % mo * ksm(sz, mo - 2) % mo);
	}
	
	return 0;
}