机器学习（课堂笔记）Day05：梯度下降法

目录

0x00 什么是梯度下降法

0x01 模拟实现梯度下降法

0x02 线性回归问题中的梯度下降法

0x03 实现线性回归中的梯度下降法

0x04 梯度下降法的向量化 和数据标准化

0x05 随机梯度下降法 Stochastic Gradient Descent

0x06 scikit-learn中的随机梯度下降法

0x07 如何确定梯度计算的准确性？调试梯度下降法

0x08 总结：

---

0x00 什么是梯度下降法

梯度下降法不是一个机器学习算法，而是一种基于搜索的最优化方法，用于求损失函数的最小值，与之相对还有梯度上升法，用于求效用函数的最大值。

一元函数中梯度就是导数，多元函数中梯度是对各元求偏导组成的列向量。

下面以一元函数为例，详细分析下一元函数的梯度下降法：

任取一点，如果该点的导数不为0，那么说明该点一定不是极值点

导数就是因变量沿x轴的变化率，变化率为正说明因变量沿该x轴正方向走会增加

变化率为负说明因变量沿x正方向走会减小

如果把变化率看成一个一维向量（从原点出发指向 x轴上对应坐标的一条向量），那么变化率指向的方向（取决于变化率的符号） 就是因变量增加的方向

那么变化率向量的反方向，就是因变量减少的方向

下图中导数为负值，说明J增大的方向是x轴的负方向，即 J(θ+ dJ/dθ） > J(θ)

那么，J(θ-η *dJ/dθ) < J(θ) ,即该点的x值减去该点的导数值 必然是向着函数值减小的方向移动的。至于移动的幅度多大，由η 来决定。η  就称为学习率，如果该值取得过大，可能导致移动幅度过大，从曲线的一头一口气移动到另一头。该值是梯度下降法的一个超参数，我们可以通过网格搜索来求得一个最佳的学习率

梯度下降法的过程可以理解为一个小球顺着山坡向下滑，这个滑动一次的步幅就由η 来决定

注意：

并不是所有函数都有唯一的极值点，例如：

如果我们只选择一次初始点，通过梯度下降法得到可能只是局部最优解，而不是全局最优解

解决方案：

多次运行，随机化初始点

所以，梯度下降法的初始点也是一个超参数

注：线性回归问题的损失函数具有唯一最优解，不需要多次运行，寻找初始点

0x01 模拟实现梯度下降法

选取0.0点为theta的初始值。然后不断循环，求导数，让theta向梯度的反方向移动即可

如果学习率选择的太大，可能导致如下情况：

0x02 线性回归问题中的梯度下降法

将梯度下降法扩展到高维：（多元函数求极值问题）

高维度下自变量 theta 不在只是一个值， 而一个向量 = （theta0,theta1,...）

复习下高数中的相关定义：

梯度▽J = J对各theta 求偏导组成的向量

函数沿l方向的变换率 = 梯度  点乘  l方向的单位方向向量el  = |梯度| * |el|*夹角余弦值= 梯度的模 * 夹角余弦值 （证明过程见高数教材）

el = （cosα，cosβ,...）其中α为l方向与第一个坐标轴的夹角，β为l方向与第二个坐标轴的夹角...

当夹角余弦值值为1 的时候，即l方向为梯度向量的方向时，函数增加最快

当夹角余弦值为-1的时候，即l方向为梯度向量相反的方向时，函数减少最快

当夹角余弦值为0的时候，即l方向与梯度向量方向正交的时候，函数的变换率为0

线性回归问题中，我们要求的是损失函数的最小值，损失函数如下：

 

那么我们首先需要需要求出损失函数的梯度向量即可，思路很简单，对该多元函数的各元求偏导，然后组合成一个列向量即可，具体求解过程如下：

其实直接用上式作为损失函数并不是很好。因为它的值和m的大小有关，其中m为训练集的元素个数，我们可以将上面的式子除以m，减弱m的影响。

即将误差平方的均值作为损失函数：

接下来我们只需要：

让自变量组成的向量沿着梯度的反方向移动，便可以逐步达到因变量的极小值

让自变量组成的向量沿着梯度方向移动，便可以逐步达到因变量的极大值

0x03 实现线性回归中的梯度下降法

注意下式中对求和公式的转化：

将需要求和的每个样本，叠加成一个向量。

然后用np.sum(该向量) 将该向量中的元素加起来即可

封装线性回归算法：

'''
Author: your name
Date: 2020-11-12 14:21:32
LastEditTime: 2020-11-14 16:04:17
LastEditors: Please set LastEditors
Description: In User Settings Edit
FilePath: /ML/playML/LinearRegression.py
'''
import numpy as np
from .metrics import r2_score


class LinearRegression:
    def __init__(self):
        self.coef_ = None  # 系数
        self.interception = None  # 截距
        self._theta = None  # θ

    def fit_normal(self, X_train, y_train):
        assert X_train.shape[0] == y_train.shape[0],\
            "X_train中的样本数量和y_train中的标记数量必须相等"
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        # 给X_train左边加上1列，全是1 => np.ones( (len(X_train),1) ) 行数和X_train一样，列数为1
        # 直接套用公式
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        # 复习一下：np.linalg.inv() 求矩阵的逆
        self.interception = self._theta[0]  # 截距就是θ的第一个元素
        self.coef_ = self._theta[1:]
        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta))**2)/len(y)
            # theta 向量 和 X 列向量 相乘 就是预测结果组成的向量
            except:
                return float('inf')

        def dJ(theta, X_b, y):  # J 对theta中的每个元素求偏导数
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = np.sum((X_b.dot(theta) - y).dot(X_b[:, i]))
            return res * 2 / len(X_b)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
            theta = initial_theta
            i_iter = 0
            while i_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta*gradient
                if(abs(J(theta, X_b, y)-J(last_theta, X_b, y)) < epsilon):
                    break
                i_iter += 1
            return theta
        X_b = np.hstack([np.ones((len(X_train),1)),X_train])
        initial_theta = np.zeros(X_b.shape[1]) #等于Xb的列数
        self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def predict(self, X_predict):
        assert self.interception is not None and self.coef_ is not None,\
            "在predict之前请先fit"
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        y_predict = X_b.dot(self._theta)
        return y_predict

    def score(self, X_test, y_test):
        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

测试：

0x04 梯度下降法的向量化 和数据标准化

上述的梯度公式还可以进一步转化：

即可以将原来的求和公式转化为两个矩阵相乘的形式，这个转化的过程就称为向量化

推导过程如下：

=   * 

  1 x m 维度 * m x（n+1） = 1 x（n+1） 一行n+1列，是一个行

向量，但是一般情况下我们使用列向量来表示梯度

所以，我们需要对该结果再进行一次转置，得到：

梯度 =  

友情提醒：X的上标i 是样本的标号，X的下标是样本特征的标号

def dJ(theta,X_b,y): #J 对theta中的每个元素求偏导数
#     res = np.empty(len(theta))
#     res[0] =np.sum(X_b.dot(theta) - y)
#     for i in range(1,len(theta)):
#         res[i] =np.sum((X_b.dot(theta) - y).dot(X_b[:,i]))
#     return res * 2 / len(X_b)
    return X_b.T.dot(X_b.dot(theta)-y) * 2. / len(X_b)

数据归一化：

梯度下降法的优势：

相比于正规方程解的方法，梯度下降法的时间复杂度更小，速度更快

0x05 随机梯度下降法 Stochastic Gradient Descent

我们之前使用的梯度下降法，每次训练/更新 参数 都需要全部样本集参与计算，这种梯度下降法称为“批量梯度下降法(Batch Gradient Descent)”。这种梯度下降法最大的缺点便是：当我们需要训练参数或者更新参数时，不得不使用全部的数据集，计算量巨大。

我们知道：

梯度方向 是 函数增大最快的方向

梯度的反方向是函数值减小最快的方向

那么如果我们随机选取一个样本，从该样本中训练中出一个方向，向该方向搜索，是否也能得到最小值呢？

如果只考虑一个样本，那么损失函数就变成了：即该样本和拟合曲线的预测值之间的差距的平方

我们想办法求该损失函数的最小值。只要我们循环足够多次，且每次循环都随机取一个样本，让该样本和拟合曲线之间差距最小，最终一定能达到整个样本 和 拟合曲线之前的差距最小。

换句话说：我们不断随机取样本点，让拟合线向这些点逼近，那么最终得到结果便是拟合线 更好的拟合所有样本点。

这种方法便称为随机梯度下降法

求该损失函数的梯度：

 

友情提醒：X的上标i 是样本的标号，X的下标是样本特征的标号

也就是说原来我们是取了所有的样本，求整体的损失函数的最小值

现在我们只是随机取出一个样本，求该单个样本损失函数的最小值，然后不断循环，让每个样本的损失函数最小，那么整体的损失函数就达到了最小值。

对随机梯度下降法来说，学习率的选取非常重要，学习率应该随着循环次数的增加而减少

比如：

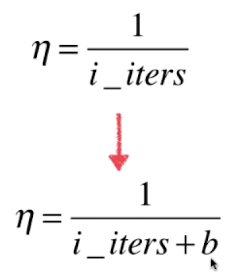
一位直接取倒数，可能导致学习率变化太快，例如：

i_iters 从1 变到2 ，学习率就从1 变到了 0.5

i_iters 从10000 变道10001，学习率才下降了1/10000

前后学习率变化幅度差别太大了

所以可以给循环次数再加一个常数，然后取倒数，例如该常数取50

i_iters 从1到2，学习率 从1/51 到1/52

i_iters 从10000 到10001 ,学习率从 1/10050 到 1/10051

同样我们的分子也可以取a，不一定取1

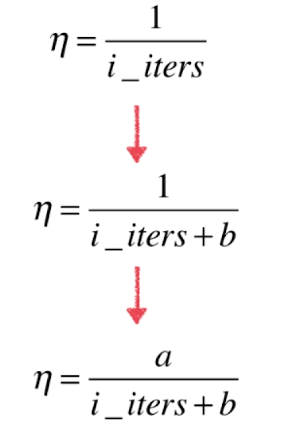
这样，a 和b 的值就成为了该算法的两个超参数

以上方法，模拟了退火的思想：

打造钢铁，火焰的温度随时间增大而减小

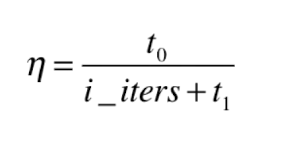
实现随机梯度下降法：

封装成函数：

    #随机梯度下降法
    def fit_sgd(self,X_train,y_train,n_iter=5,t0=5,t1=50):
        #计算梯度方向
        def dJ_sgd(theta,X_b_i,y_i):
            return X_b_i * (X_b_i.dot(theta)-y_i) *2
        def sgd(X_b,y,initial_theta,n_iters,t0=5,t1=50):
            def learning_rate(t):
                return t0/(t+t1)
            theta = initial_theta
            m = len(X_b)
            #n_iter表示需要将所有的样本循环几遍
            for cur_iter in range(n_iters*m):
                indexes = np.random.permutation(m) #对样本的索引进行乱序排序
                X_b_new = X_b[indexes]
                y_new = y[indexes]
                for i in range(m):
                    gradient = dJ_sgd(theta,X_b_new[i],y_new[i])
                    theta = theta - learning_rate(cur_iter*m+i)*gradient
            return theta
        X_b = np.hstack([np.ones((len(X_train),1)),X_train])
        initial_theta = np.zeros(X_b.shape[1]) #等于Xb的列数
        self._theta = sgd(X_b,y_train,initial_theta,n_iter)
        self.interception = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

0x06 scikit-learn中的随机梯度下降法

0x07 如何确定梯度计算的准确性？调试梯度下降法

调试思路：

用一种更简单更可靠的方法去求偏导，进而得到梯度。（虽然这种方法的时间复杂度比较高）

然后用我们数学推导的公式去求梯度，然后用一个较小的数据集测试两者得到的结果。如果得到的结果差不多，就说明我们推导的梯度求导公式没有问题。

下面来介绍这种简单可靠的求偏导的思路：

J(theta)函数的导数近似等于 theta前后各取一点得到的割线的斜率

低维情况下：

推广到高维情况下，求偏导

程序实现：

0x08 总结：

之前我们讨论了：

批量梯度下降法（Batch Gradient Descent）: 一次拟合所有的样本

随机梯度下降法（Stochastic Gradient Descent）:一次只随机拟合一个样本，拟合多次达到拟合所有样本的效果

那么能不能将两者综合起来呢？这便是小批量梯度下降法。感兴趣可以自己实现这种梯度下降法

再次强调一下：梯度下降法不是一个机器学习领域的算法，而是一种基于搜索的最优化方法，我们可以用它来最小化一个损失函数