原文链接:矩阵的Cholesky分解
首先来复习线性代数中几个重要的概念。
1)如果一个复矩阵A = A*(共轭转置),则A称为Hermitian矩阵。(注意,矩阵A转置后仍为其本身,显然A一定是方阵。)
2)关于正定矩阵的定义:
- Mn×n 是一个对称的实矩阵,对于任意的(由n个实数组成)的非零列向量z,都有 zTMz > 0,则称M是正定的(positive definite)的。
- More generally,Mn×n 是一个Hermitian矩阵,对于任意的(由n个复数组成)的非零列向量z,都有 z*Mz > 0,则称M是正定的。
实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零。实二次型矩阵(注意二次型矩阵必然也是对称矩阵)为正定二次型的充要条件是的矩阵的特征值全大于零。
矩阵的Cholesky分解
如果矩阵A是正定的,那么它可以被(唯一地)分解为一个下三角矩阵L和其共轭转置L*的乘积,这就是所谓的“矩阵的Cholesky分解”。对于实矩阵而言,即 A =LLT,其中L是一个下三角矩阵。下面是一个3×3的矩阵Cholesky分解的示意。
具体要如何来计算Cholesky分解的值呢?通过观察,结合矩阵乘法的规则,不难发现矩阵L对角线上的元素可以由如下规律算得:
推广后得到:
对于那些位于对角线以下的元素lik,其中i>k,则会有下面这样的计算规律:
仍然可以推广得到一个更加普适的公式:
在数学软件/工具中计算矩阵的Cholesky分解
当然了,在很多数学软件或工具中都已经内置了现成的函数,我们并不需要手动去执行那些繁琐的计算。下面来看一个具体的例子:
首先在R中来验证上面的Cholesky分解结果。注意函数chol返回的是一个上三角矩阵,如果要得到下三角矩阵只要对该结果做一下转置处理即可。
> m = matrix(c(4, 12, -16, 12, 37, -43, -16, -43, 98), nrow=3, ncol=3)
> m
[,1] [,2] [,3]
[1,] 4 12 -16
[2,] 12 37 -43
[3,] -16 -43 98
> chol(m)
[,1] [,2] [,3]
[1,] 2 6 -8
[2,] 0 1 5
[3,] 0 0 3>> A = [4 12 -16
12 37 -43
-16 -43 98];
>> [L] = chol(A,'lower')
L =
<span class="hljs-number">2</span> <span class="hljs-number">0</span> <span class="hljs-number">0</span>
<span class="hljs-number">6</span> <span class="hljs-number">1</span> <span class="hljs-number">0</span>
-<span class="hljs-number">8</span> <span class="hljs-number">5</span> <span class="hljs-number">3</span></code></pre><span style="font-size:18px;">而且,你还可以验证原对称矩阵是正定的。如下可见,矩阵的三个特征值都是大于零的。</span><pre><code class="language-ruby"><span class="hljs-meta">>></span> [v,d]=eig(A)
v =
<span class="hljs-number">0</span>.<span class="hljs-number">9634</span> <span class="hljs-number">0</span>.<span class="hljs-number">2127</span> -<span class="hljs-number">0</span>.<span class="hljs-number">1630</span>
-0.2648 0.8490 -0.4573
0.0411 0.4838 0.8742
d =
<span class="hljs-number">0</span>.<span class="hljs-number">01</span>88 <span class="hljs-number">0</span> <span class="hljs-number">0</span>
<span class="hljs-number">0</span> <span class="hljs-number">15.5040</span> <span class="hljs-number">0</span>
<span class="hljs-number">0</span> <span class="hljs-number">0</span> <span class="hljs-number">123.4772</span></code></pre><font>最后一个问题,Cholesky分解在实际中有什么用?其中一个非常重要的应用就是解方程组 <strong>A</strong><em><span style="font-family:'Times New Roman';">x </span></em>= <strong>B</strong>,其中<span style="font-size:18px;"><strong>A</strong></span>是一个正定矩阵。因为<span style="font-size:18px;"><span style="font-size:18px;"><strong>A</strong></span>是一个正定矩阵</span>,所以有<span style="font-size:18px;"><span style="font-size:18px;"><strong>A</strong></span> =<span style="font-size:18px;"><strong>L</strong></span><span style="font-size:18px;"><strong>L<span style="font-size:18px;"><span style="font-size:14px;"><sup>T</sup></span></span></strong></span>,其中<span style="font-size:18px;"><span style="font-size:18px;"><strong>L</strong></span></span>是<span style="font-size:18px;">一个下三角矩阵</span></span>。原方程组可以写成 <font><span style="font-size:18px;"><span style="font-size:18px;"><strong>L</strong></span><span style="font-size:18px;"><strong>L<span style="font-size:18px;"><span style="font-size:14px;"><sup>T</sup></span></span></strong></span><span style="font-size:18px;"><em><span style="font-family:'Times New Roman';">x </span></em>= <strong>B</strong></span></span></font>。如果令 y = <font><font><span style="font-size:18px;"><span style="font-size:18px;"><strong>L<span style="font-size:18px;"><span style="font-size:14px;"><sup>T</sup></span></span></strong></span><span style="font-size:18px;"><em><span style="font-family:'Times New Roman';">x </span></em></span></span></font></font>,则有<font><span style="font-size:18px;"><span style="font-size:18px;"><span style="font-size:18px;"><strong>L</strong></span><span style="font-size:18px;"><span style="font-family:Arial;">y</span><em><span style="font-family:'Times New Roman';"> </span></em>= <strong>B</strong></span></span></span>。注意到<span style="font-size:18px;"><font>其中<span style="font-size:18px;"><span style="font-size:18px;"><strong>L</strong></span></span>是<font>一个下三角矩阵,所以从下向上求解y是非常非常容易的!求解出y之后,在按照类似的方法求解<font>y = <font><font><span style="font-size:18px;"><span style="font-size:18px;"><strong>L<span style="font-size:18px;"><span style="font-size:14px;"><sup>T</sup></span></span></strong></span><span style="font-size:18px;"><em><span style="font-family:'Times New Roman';">x </span></em></span></span></font></font></font>中的 <span style="font-family:'Times New Roman';"><em>x</em></span>,而其中<font><font><span style="font-size:18px;"><font><font><font><font><font><span style="font-size:18px;"><span style="font-size:18px;"><strong>L<span style="font-size:18px;"><span style="font-size:14px;"><sup>T</sup></span></span></strong></span></span></font></font></font></font></font></span></font></font>是一个上三角矩阵,所以最终求出 <span style="font-family:'Times New Roman';"><em>x </em></span>就也是非常非常容易的!</font></font></span></font></font><br><p></p><p><strong><br></strong></p><p><span style="font-size:18px;"><strong>参考文献与其他推荐阅读材料</strong></span></p><p><span style="font-size:18px;"><strong><br></strong></span></p><p><span style="font-size:18px;">1)关于 Hermitian矩阵,可以参考<span style="font-size:18px;">《<span class="link_title"><a href="http://blog.csdn.net/baimafujinji/article/details/6478420">线性代数笔记(6):内积空间(下) </a></span>》</span></span></p><p><span style="font-size:18px;">2)关于二次型,可以参考<span style="font-size:18px;">《<span class="link_title"><a href="http://blog.csdn.net/baimafujinji/article/details/51167852">Hessian矩阵与多元函数极值 </a></span>》</span></span><br></p><p><span style="font-size:18px;">3)http://rosettacode.org/wiki/Cholesky_decomposition<br></span></p><p><span style="font-size:18px;"><br></span></p><p><span style="font-size:18px;"><strong>(本文完)</strong></span></p> </div><div><div></div></div>
</div>








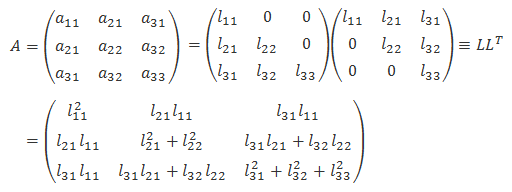

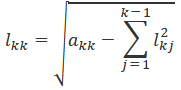


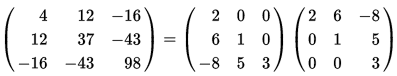













 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








