棋盘路径计数算法-CSDN博客

本文链接：https://blog.csdn.net/weixin_43519514/article/details/106804044

题目：

请编写一个函数（允许增加子函数），计算n x m的棋盘格子（n为横向的格子数，m为竖向的格子数）沿着各自边缘线从左上角走到右下角，总共有多少种走法，要求不能走回头路，即：只能往右和往下走，不能往左和往上走。

输入输出：

输入描述: 输入两个正整数n ,m

输出描述: 返回结果

题解：

这道题从左上角到右下角，不是走格子，而是选择边缘线，这个比较特殊，我们只能尝试找一下规律。

当只有一个格子的时候（n=1,m=1）

我们尝试着增加格子：

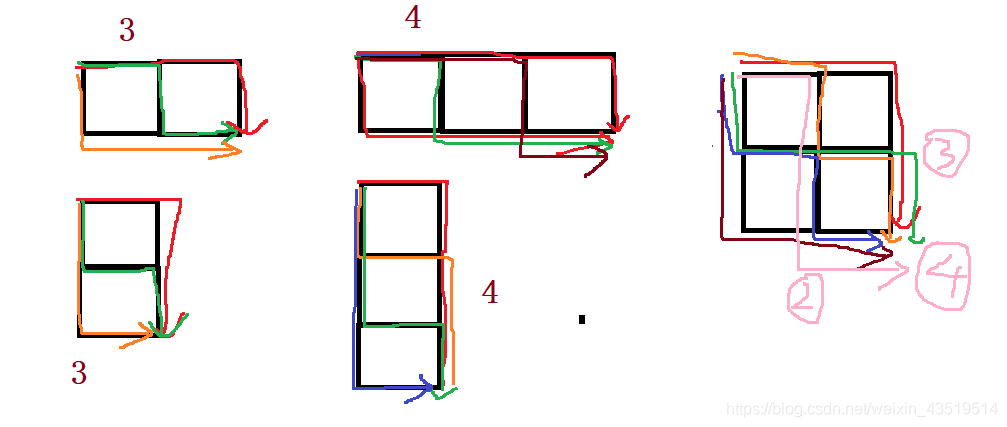
我们可已从以上的图中发现这样的一个规律：

当只有一列的时候有多少个横线就有多少种方法：横线条数为n+1，而此时m=1；所以这种情况下有n+m中方法到达右下角

只有一行的时候，情况类似，方法数也为n+m

即总结上面的两种情况 n=1或者m=1的时候，有n+m种情况

当n>1且m>1的时候，上面的规律就不太适用了。

但是我们图中发现4号位置方法数量是三号位置的方法数量和2号位置的方法数量之和：而2号方法数和3号位置方法数我们是可以计算的！

但是其他的情况适用嘛：我们来递推一下

我们用3*3的方格为例：1后位置可以有3号位置和2号位置之和。。。。。。。

有递推过程太长太复杂，我们直接看左边的图，三号位置有5号位置和4号位置计算出来，这是没问题的；

2号位置我们可以计算，前面证明过也没什么问题。

2号位置和3号位置到达1号位置各自只有一种方法。所以1号位置通过2号和3号位置计算也是没有任何问题的。

如果我们放大，递推过程没有问题！

所以

dp(n,m)=dp(n-1,m)+dp(m-1,n);

下面我们就可以看代码了：

代码：动态规划

int Pathsum(int n, int m)
{
	if (n == 0 || m == 0)
		return 0;
	vector<vector<int>> dp(n + 1, vector<int>(m + 1));

	for (int i = 1; i<n + 1; ++i)
	{
		for (int j = 1; j<m + 1; ++j)
		{   //仅有一行或者一列的情况
			if (i == 1 || j == 1)
				dp[i][j] = i + j;
			else
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
		}
	}
	return dp[n][m];
}

化简之后：空间复杂度O（m）

int Pathsum(int n, int m)
{
	if (n == 0 || m == 0)
		return 0;
	vector<int>dp(m + 1);
	int k = 1;
	while (k<n + 1)
	{
		for (int i = 1; i<m + 1; ++i)
		{
			if (k == 1 || i == 1)
				dp[i] = k + i;
			else
				dp[i] = dp[i - 1] + dp[i];

		}
		k++;
	}
	return dp[m];
}

递归方法：

int Pathsum(int n,int m)
{
    if(n==0||m==0)
        return 0;
      if(n==1||m==1)
          return n+m;
      else
          return Pathsum(n-1,m)+Pathsum(n,m-1);
}


int main()
{
    int n,m;
    while(cin>>n>>m)
    cout<<Pathsum(n,m)<<endl;
    return 0;
}