ch9 - 动态规划（上）

目录：

1. 一道题理解动态规划 - triangle
   1.1 遍历的方法 - DFS：traverse
   1.2 遍历的方法 - DFS：divide conquer
   1.3 记忆化搜索 - divide conquer + Memorization
   1.4 动态规划 - 自顶向下、自底向上
2. 记忆化搜索的本质：动态规划
3. 什么情况下使用动态规划？ 什么情况下不使用动态规划？
4. 动态规划的四要素 vs 递归三要素

1. 一道题理解动态规划 - triangle

1). 题目
http://www.lintcode.com/zh-cn/problem/triangle/
给定一个数字三角形，找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上。

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]？
]

和“二叉树从根结点出发，走到叶子的路径和最大的路径”，区别：

• 1） 二叉树每个点处理的时间复杂度是O(1)，且每个点被进入一次。从根节点到某一点只有一条路径，而三角形中根节点到每个节点有多条路径；
• 2） 二叉树的节点个数是： 2^h-1, 三角形的节点个数是：h^2
• 3） 对二叉树来说，n指的是节点个数， 对三角形来说，n指的是三角形的高度，习惯问题
  
  
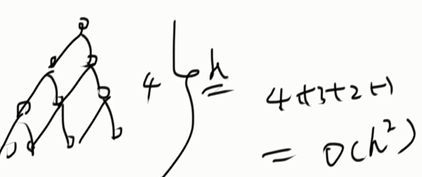
  2）解决方法
  DFS：traverse
  DFS：divide conquer
  divide conquer + Memorization
  traditionmal dp

A.遍历的方法 - DFS：traverse
a. 定义函数接口：需要传入当前位置、到某个点之前的路径和（到某个点包含该点的路径和）。
b. 判断函数出口：x==n，表示走到了最后一行
c. 递归下去

时间复杂度：O(2^n)
超时：TLE

class Solution {
public:
    /*
     * @param triangle: a list of lists of integers
     * @return: An integer, minimum path sum
     */
    int minimumTotal(vector<vector<int>> &triangle) {
        // write your code here
        if(triangle.size()==0){
            return 0;
        }

        int best = INT_MAX;
        traverse(triangle, 0, 0, 0, best);

        return best;
    }

    //sum = root->x,y 但不包含x,y的路径和
    void traverse(vector<vector<int>> &triangle, int x, int y, int sum, int &best){
        if(x==triangle.size()){
            best = min(sum, best);
            return;
        }

        traverse(triangle, x+1, y, sum+triangle[x][y], best);
        traverse(triangle, x+1, y+1, sum+triangle[x][y], best);
    }
};

B. 分治法 - DFS：divide conquer
递归三要素：
a 递归定义：寻找一条从x,y出发，到底层的最短路径。
b 递归拆解：将一个大问题拆解为两个小问题，即从(x+1,y)到底层，从（x+1,y+1）到底层的最小值。
c 递归的出口：

时间复杂度：O(2^n)

超时：TLE

class Solution {
public:
    /*
     * @param triangle: a list of lists of integers
     * @return: An integer, minimum path sum
     */
    int minimumTotal(vector<vector<int>> &triangle) {
        // write your code here
        if(triangle.size()==0){
            return 0;
        }

        return divideConquer(triangle, 0, 0);
    }

    //递归定义：寻找一条从x,y出发，到底层的最短路径
    int divideConquer(vector<vector<int>> &triangle, int x, int y){
        if(x==triangle.size()){
            return 0;
        }
        return triangle[x][y]+min(divideConquer(triangle,x+1,y), divideConquer(triangle,x+1,y+1));
    }
};

3). divide conquer + Memorization （记忆化搜索的本质：动态规划）
有重复计算，用hash表记录重复使用的位置，每个位置表示从该位置出发到最底层的最短路径，如下图：
时间复杂度：O(n^2)

class Solution {
public:
    /*
     * @param triangle: a list of lists of integers
     * @return: An integer, minimum path sum
     */
    int minimumTotal(vector<vector<int>> &triangle) {
        // write your code here
        if(triangle.size()==0){
            return 0;
        }

        int n = triangle.size();
        vector<vector<int>> hash(n,vector<int>(n,INT_MAX));

        return divideConquer(triangle, hash, 0, 0);
    }

    int divideConquer(vector<vector<int>> &triangle, vector<vector<int>> &hash, int x, int y){
        if(x==triangle.size()){
            return 0;
        }

        if(hash[x][y] != INT_MAX){
            return hash[x][y];
        }

        return triangle[x][y]+min(divideConquer(triangle,hash, x+1,y), divideConquer(triangle,hash, x+1,y+1));
    }
};

4). traditionmal dp 动规
A. 自底向上
B. 自顶向下

 class Solution {
    public:
        /*
         * @param triangle: a list of lists of integers
         * @return: An integer, minimum path sum
         */
        int minimumTotal(vector<vector<int>> &triangle) {
            // write your code here
            int n = triangle.size();
            vector<vector<int>> f(n,vector<int>(n,0));
    
            for(int i=0;i<n;++i){
                f[n-1][i] = triangle[n-1][i];
            }
    
            for(int i=n-2;i>=0;--i){
                for(int j=0;j<=i;++j){
                    f[i][j] = triangle[i][j] + min(f[i+1][j], f[i+1][j+1]);
                }
            }
    
            return f[0][0];
        }
    };

---

class Solution {
    public:
        /*
         * @param triangle: a list of lists of integers
         * @return: An integer, minimum path sum
         */
        int minimumTotal(vector<vector<int>> &triangle) {
            // write your code here
            int n = triangle.size();
            vector<vector<int>> f(n,vector<int>(n,0));
    
            f[0][0] = triangle[0][0];
    
            for(int i=1;i<n;++i){
                f[i][0] = triangle[i][0] + f[i-1][0];
                f[i][i] = triangle[i][i] + f[i-1][i-1];
            }
    
            for(int i=1;i<n;++i){
                for(int j=1;j<i;++j){
                    f[i][j] = triangle[i][j] + min(f[i-1][j], f[i-1][j-1]);
                }
            }
    
            int res = INT_MAX;
            for(int i=0;i<n;++i){
                res = min(res, f[n-1][i]);
            }
    
            return res;
        }
    };

2. 记忆化搜索的本质：动态规划

1）动规为什么快？ 去掉了重复计算

2）动规与分治法的区别？ - 是否有重复计算，分治法是没有重复交集的，比如二叉树上的分治，左子树与右子树没有重复部分，所以二叉树上的都不是动态规划，动态规划是有交集的。

3）动态规划有两种实现方法：

A. 多重循环：自底向上与自顶向下
优点：正规，大多数面试官可以接受，存在空间优化可能性
缺点：思考有难度
举例：
B. 记忆化搜索
优点：容易从搜索算法直接转化过来。有的时候可以节省更多时间。搜索+hash表 -> dp
缺点：递归
举例：上例1.1

4）多重循环有两种实现方法：
时间复杂度和空间复杂度都是O(n^2)，两个方法没有太大优劣区别，一个正向一个逆向。

A. 自底向上的实现方法

B. 自顶向下的实现方法

3. 什么情况下使用动态规划？ 什么情况下不使用动态规划？

满足以下三个条件之一极有可能使用dp，不是一定

• 求最大最小值
• 判断是否可行 （大概率）
• 统计方案个数 （大概率） （除n皇后）

满足以下三个条件之一极不可能使用dp，第二点除了背包可能是一个集合

4. 动态规划的四要素 vs 递归三要素

第一个要素是最难的，所以其他部分都是可推导的