SVM模型（理论知识1）

前言

支持向量机（support vector machine，SVM）是有监督学习中最有影响力的机器学习算法之一，典型应用是解决手写字符识别问题。

支持向量机是一种二分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

支持向量机的学习算法是求解凸二次规划的最优化算法。基础的SVM算法是一个二分类算法，至于多分类任务，可以通过多次使用SVM进行解决。

SVM模型介绍

超平面

超平面的理解：在一维空间中，如需将数据切分为两段，只需要一个点即可；在二维空间中，对于线性可分的样本点，将其切分为两类，只需一条直线即可；在三维空间中，将样本点切分开来，就需要一个平面。

距离计算

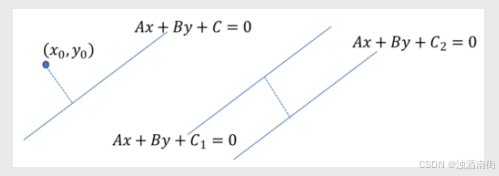
点到线的距离：
$$d=\frac{|A_{x0}+B_{y0}+C|}{\sqrt{A^2+B^2}}$$
平行线间的距离：
$$d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}$$

思想介绍

图中绘制了两条分割直线，利用这两条直线，可以方便地将样本点所属的类别判断出来。虽然从直观来看这两条分割线都没有问题，但是哪一条直线的分类效果更佳呢(训练样本点的分类效果一致，并不代表测试样本点的分类效果也一样)？甚至于在直线l1和l2之间还存在无数多个分割直线，那么在这么多的分割线中是否存在一条最优的“超平面”呢？

假设直线$l_i$是$l_1$和$l_2$之间的某条直线(分割面)，为了能够寻找到最优的分割面$l_i$,需要做三件事，首先计算两个类别中的样本点到直线$l_i$的距离，然后从两组距离中各挑选出一个最短的（如图中所示的距离$d_1$和$d_2$）,继续比较$d_1$和$d_2$,再选出最短的距离（如图中的$d_1$）,并以该距离构造“分割带”，(如图中经平移后的两条虚线)；最后利用无穷多个分割直线$l_i$,构造无穷多个分割带，并从这些分割带中挑选出带宽最大的$l_i$。

分隔带

“分割带”代表了模型划分样本点的能力或可信度，“分割带”越宽，说明模型能够将样本点划分得越清晰，进而保证模型泛化能力越强，分类的可信度越高；反之，“分割带”越窄，说明模型的准确率越容易受到异常点的影响，进而理解为模型的预测能力越弱，分类的可信度越低。