[学习笔记] fhq Treap 平衡树

Bamboo_Day

已于 2023-08-31 11:19:19 修改

阅读量340

点赞数 1

分类专栏：随笔 C++入门基础教程文章标签：学习笔记数据结构

于 2023-08-30 19:33:55 首次发布

本文链接：https://blog.csdn.net/weixin_43617116/article/details/132585057

版权

C++入门基础教程同时被 2 个专栏收录

27 篇文章 26 订阅

订阅专栏

随笔

26 篇文章 0 订阅

订阅专栏

fhq Treap 也叫无旋Treap （好像？我也不知道）

~~反正我带旋 Treap 是不会滴，其他的平衡树也不会~~（但是会平板电视）

fhq Treap 好写，码量小，缺点是常数比较大

定义

二叉搜索树

二叉搜索树是一种二叉树的树形数据结构，其定义如下：

空树是二叉搜索树。
若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。
若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。
二叉搜索树的左右子树均为二叉搜索树。

~~至于二叉搜索树怎么写我也不知道~~

但是由于可以构造数据使得二叉搜索树退化成一条链所以平衡树就应运而生了

平衡树是通过左旋和右旋~~各种奇怪的操作~~使左子树和右子树的高度最多相差 1 的二叉搜索树

Treap 就是一种弱平衡的平衡树

Treap 顾名思义就是 Tree + Heap 是加入了堆来防止二叉搜索树退化（~~说白了就是随机化~~）

其中，二叉搜索树的性质是：

左子节点的值（ $\textit{val}$ ）比父节点大
右子节点的值（ $\textit{val}$ ）比父节点小（当然这也是可以反过来的）

堆的性质是：

子节点值（ $\textit{key}$ ）比父节点大或小（取决于是小根堆还是大根堆）
不难看出，如果用的是同一个值，那这两种数据结构的性质是矛盾的，所以我们再在搜索树的基础上，引入一个给堆的值 $\textit{key}$ 。对于 $\textit{val}$ 值，我们维护搜索树的性质，对于 $\textit{key}$ 值，我们维护堆的性质。其中 $\textit{key}$ 这个值是随机给出的。

搬个 OI-Wiki 的图片
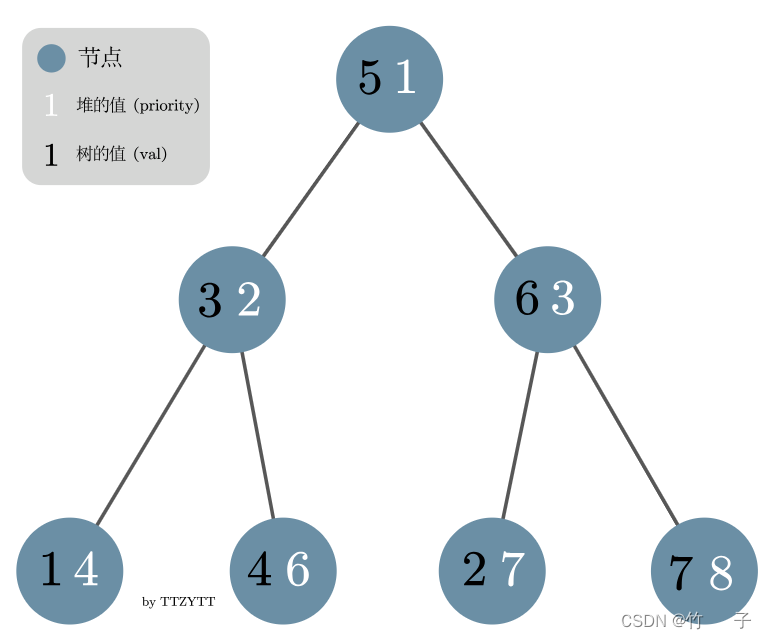
在这里插入图片描述
Treap 的核心操作是左旋和右旋而 fhq Treap 则是不带旋的 Treap,很多情况下会一些操作好写很多

fhq Treap

fhq Treap 的核心操作是分裂 ( $s pl i t$ ) 和合并 ( $m er g e$ )

节点信息

一个节点中的信息应该很好想罢，值 $v a l$ ，键值 $k ey$ ，左儿子 $l$ ，右儿子 $r$ 以及子树大小 $s i z$

struct treap{
	int val,key,siz,l,r;
}fhq[N << 1];

建立新节点

建立一个新节点其实就是把一个节点初始化掉

int new_treap(int val){
	fhq[++cnt].val = val;
	fhq[cnt].key = rand();
	fhq[cnt].siz = 1;
	return cnt;
}

很好理解对吧

更新父节点信息

其实就和线段树的 $push \_ up$ 操作是一样的

void push_up(int pos){
	fhq[pos].siz = fhq[fhq[pos].l].siz + fhq[fhq[pos].r].siz + 1;
}

分裂

分裂操作有两种，一种是按值分裂，把所有值小于等于 $v a l$ 的分裂成一颗树，把值 大于 $v a l$ 的分裂成一颗树；一种是按大小分裂，把小于等于给定大小的分裂成一棵树，大于给定大小的分裂成一颗树

一般把 fhq Treap 当正常平衡树使用的时候都是用按值分裂

直接看代码理解罢

void split(int pos, int val, int& x, int& y){//因为是一棵树分裂成两颗树，返回pair会比较麻烦，所以直接引用一下 
	if(!pos) {//到底了不能分裂 
		x = y = 0;
		return;
	}
	if(fhq[pos].val <= val){//小于val的分裂到x树去 
		x = pos;
		split(fhq[pos].r, val, fhq[pos].r, y);//右子树继续分裂 
	}else{
		y = pos;//大于val到y树去 
		split(fhq[pos].l,val,x,fhq[pos].l);//左子树继续分裂 
	}
	push_up(pos);
}

合并

合并当然就是分裂反过来噜~~

int merge(int x, int y){//注意这里x树是分裂出来小的那个树 
	if(!x || !y) return x+y;//如果x为空就返回y，如果y没有就返回x，如果两个都没有就返回0 
	if(fhq[x].key > fhq[y].key){//x的键值大，y并到x的右子树去 
		fhq[x].r = merge(fhq[x].r, y);
		push_up(x);
		return x;
	}else{
		fhq[y].l = merge(x,fhq[y].l);//y的键值大，x并到y的左子树去 
		push_up(y);
		return y;
	}
}

平衡树常规操作

前面两个操作就很短对吧，后面还要短

插入一个值 val

插入分两步

把树按 $v a l$ 分裂成两棵树
把 $v a l$ 和小于等于 $v a l$ 那棵树合并，再合并回去

void insert(int val){
	int x,y;
	split(root,val,x,y);
	root = merge(merge(x,new_treap(val)),y);
}

删除一个值 val

删除分为三步

按 $v a l$ 分裂成两棵树
把小于等于 $v a l$ 的那棵树再按 $v a l - 1$ 分裂成两棵树（这样我们就得到了全是 $v a l$ 的一棵树）
把全是 $v a l$ 的那棵树的根节点删掉（合并左子树和右子树就可以了）
把剩下的树按顺序合并回去

void del(int val){
   int x,y,z;
   split(root,val,x,z);
   split(x,val-1,x,y);
   y = merge(fhq[y].l,fhq[y].r);
   root = merge(merge(x,y),z);
}

查询 val 的排名

这个也很简单啊，就两步

把树按 $v a l - 1$ 分裂
小的那棵树的 $s i z + 1$ 就可以了
记得合并回去

void get_rank(int val){
	int x,y;
	split(root,val-1,x,y);
	cout << fhq[x].siz+1 << endl;
	root = merge(x,y);
}

查询排名为 rank 的值

这个稍微麻烦一点

void get_num(int rank){
	int now = root;
	while(now){
		if(fhq[fhq[now].l].siz+1 == rank) break;
		else if(fhq[fhq[now].l].siz >= rank) now = fhq[now].l;
		else{
			rank -= fhq[fhq[now].l].siz+1;
			now = fhq[now].r;
		}
	}
	cout << fhq[now].val << endl;
}

查找前驱/后继

void pre(int val){
	int x,y;
	split(root,val-1,x,y);
	int now = x;
	while(fhq[now].r) now = fhq[now].r;
	cout << fhq[now].val << endl;
	root = merge(x,y);
}
void nxt(int val){
	int x,y;
	split(root,val,x,y);
	int now = y;
	while(fhq[now].l){
		now = fhq[now].l;
	}
	cout << fhq[now].val << endl;
	root = merge(x,y);
}

板子传送门

Code

#include <bits/stdc++.h>
const int N = 1e5+10;
using namespace std;
struct treap{
	int val,key,siz,l,r;
}fhq[N << 1];
int cnt = 0,root;
int new_treap(int val){
	fhq[++cnt].val = val;
	fhq[cnt].key = rand();
	fhq[cnt].siz = 1;
	return cnt;
}
void push_up(int pos){
	fhq[pos].siz = fhq[fhq[pos].l].siz + fhq[fhq[pos].r].siz + 1;
}
void split(int pos, int val, int& x, int& y){//因为是一棵树分裂成两颗树，返回pair会比较麻烦，所以直接引用一下 
	if(!pos) {//到底了不能分裂 
		x = y = 0;
		return;
	}
	if(fhq[pos].val <= val){//小于val的分裂到x树去 
		x = pos;
		split(fhq[pos].r, val, fhq[pos].r, y);//右子树继续分裂 
	}else{
		y = pos;//大于val到y树去 
		split(fhq[pos].l,val,x,fhq[pos].l);//左子树继续分裂 
	}
	push_up(pos);
}
int merge(int x, int y){//注意这里x树是分裂出来小的那个树 
	if(!x || !y) return x+y;//如果x为空就返回y，如果y没有就返回x，如果两个都没有就返回0 
	if(fhq[x].key > fhq[y].key){//x的键值大，y并到x的右子树去 
		fhq[x].r = merge(fhq[x].r, y);
		push_up(x);
		return x;
	}else{
		fhq[y].l = merge(x,fhq[y].l);//y的键值大，x并到y的左子树去 
		push_up(y);
		return y;
	}
}
void insert(int val){
	int x,y;
	split(root,val,x,y);
	root = merge(merge(x,new_treap(val)),y);
}
void del(int val){
	int x,y,z;
	split(root,val,x,z);
	split(x,val-1,x,y);
	y = merge(fhq[y].l,fhq[y].r);
	root = merge(merge(x,y),z);
}
void get_rank(int val){
	int x,y;
	split(root,val-1,x,y);
	cout << fhq[x].siz+1 << endl;
	root = merge(x,y);
}
void get_num(int rank){
	int now = root;
	while(now){
		if(fhq[fhq[now].l].siz+1 == rank) break;
		else if(fhq[fhq[now].l].siz >= rank) now = fhq[now].l;
		else{
			rank -= fhq[fhq[now].l].siz+1;
			now = fhq[now].r;
		}
	}
	cout << fhq[now].val << endl;
}
void pre(int val){
	int x,y;
	split(root,val-1,x,y);
	int now = x;
	while(fhq[now].r) now = fhq[now].r;
	cout << fhq[now].val << endl;
	root = merge(x,y);
}
void nxt(int val){
	int x,y;
	split(root,val,x,y);
	int now = y;
	while(fhq[now].l){
		now = fhq[now].l;
	}
	cout << fhq[now].val << endl;
	root = merge(x,y);
}
int n;

int main(){
	cin >> n;
	while(n--){
		int op,x;
		cin >> op >> x;
		if(op == 1){
			insert(x);
		}
		if(op == 2){
			del(x);
		}
		if(op == 3){
			get_rank(x);
		}
		if(op == 4){
			get_num(x);
		}
		if(op == 5){
			pre(x);
		}
		if(op == 6){
			nxt(x);
		}
	}	
	return 0;
}

感觉只实现这些不够？那可以去看看下一篇fhq 实现文艺平衡树

如果有任何不足之处或者疑问，欢迎在评论区提出

Bamboo_Day

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
打赏
0
评论
[学习笔记] fhq Treap 平衡树

二叉搜索树是一种二叉树的树形数据结构，其定义如下：空树是二叉搜索树。若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。二叉搜索树的左右子树均为二叉搜索树。至于二叉搜索树怎么写我也不知道但是由于可以构造数据使得二叉搜索树退化成一条链所以平衡树就应运而生了平衡树是通过左旋和右旋各种奇怪的操作使左子树和右子树的高度最多相差 1的二叉搜索树Treap 就是一种弱平衡的平衡树。
复制链接

扫一扫