计算机器视觉（五）

Hough transform补充

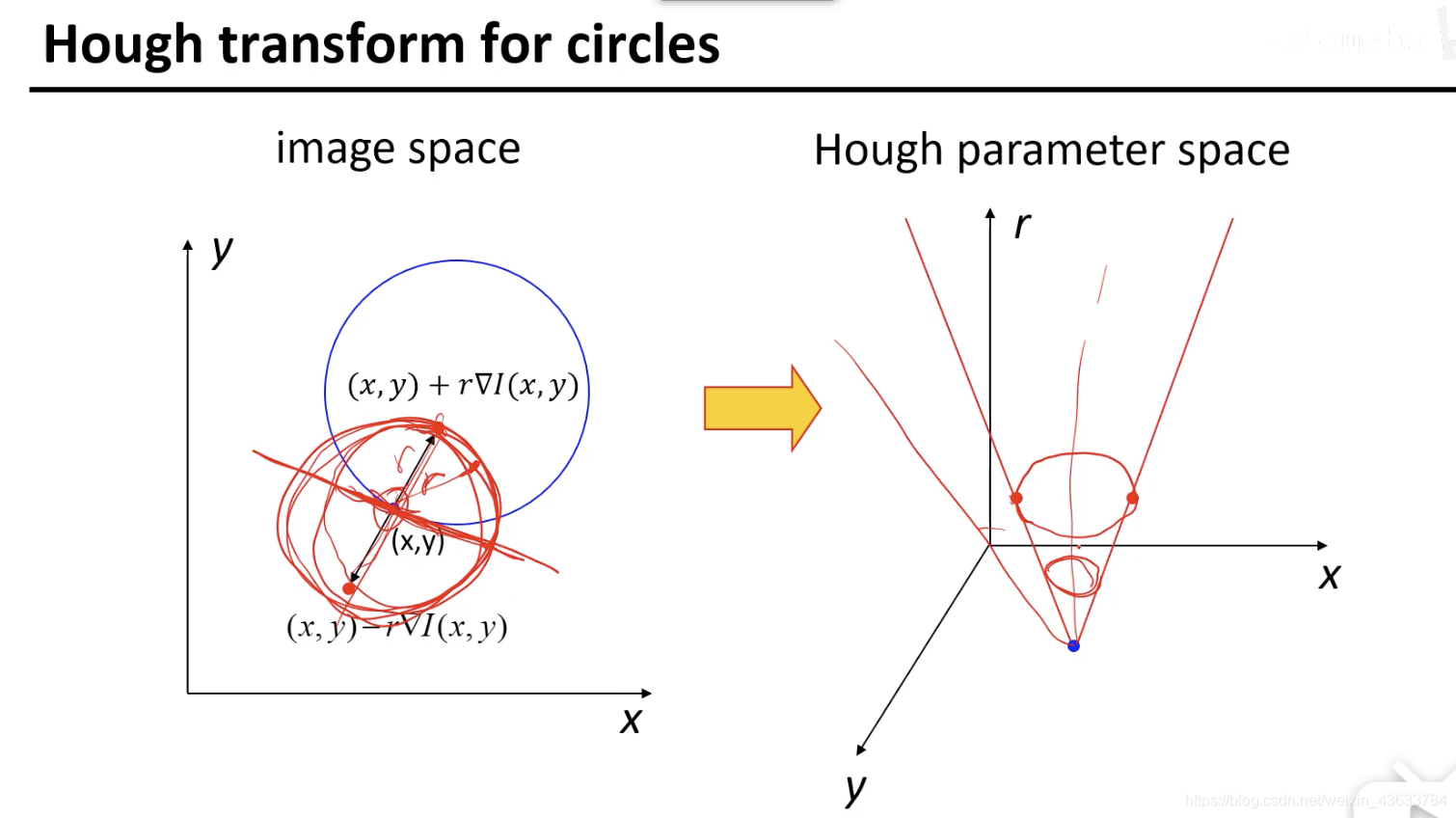
如果这里的（x,y)的方向不给定的话，每确定一个半径r的值就会在image space上画出一个圆，那假设现在确定的r之一是r0，那（x，y）在Hough parameter space上进行投票就是一个圆（也就是一个点对应一个圆），那么整个image space中的圆上的所有点（x，y）对应的就是Hough parameter space中的一个锥面。每个点一个锥体？？？？【为啥】

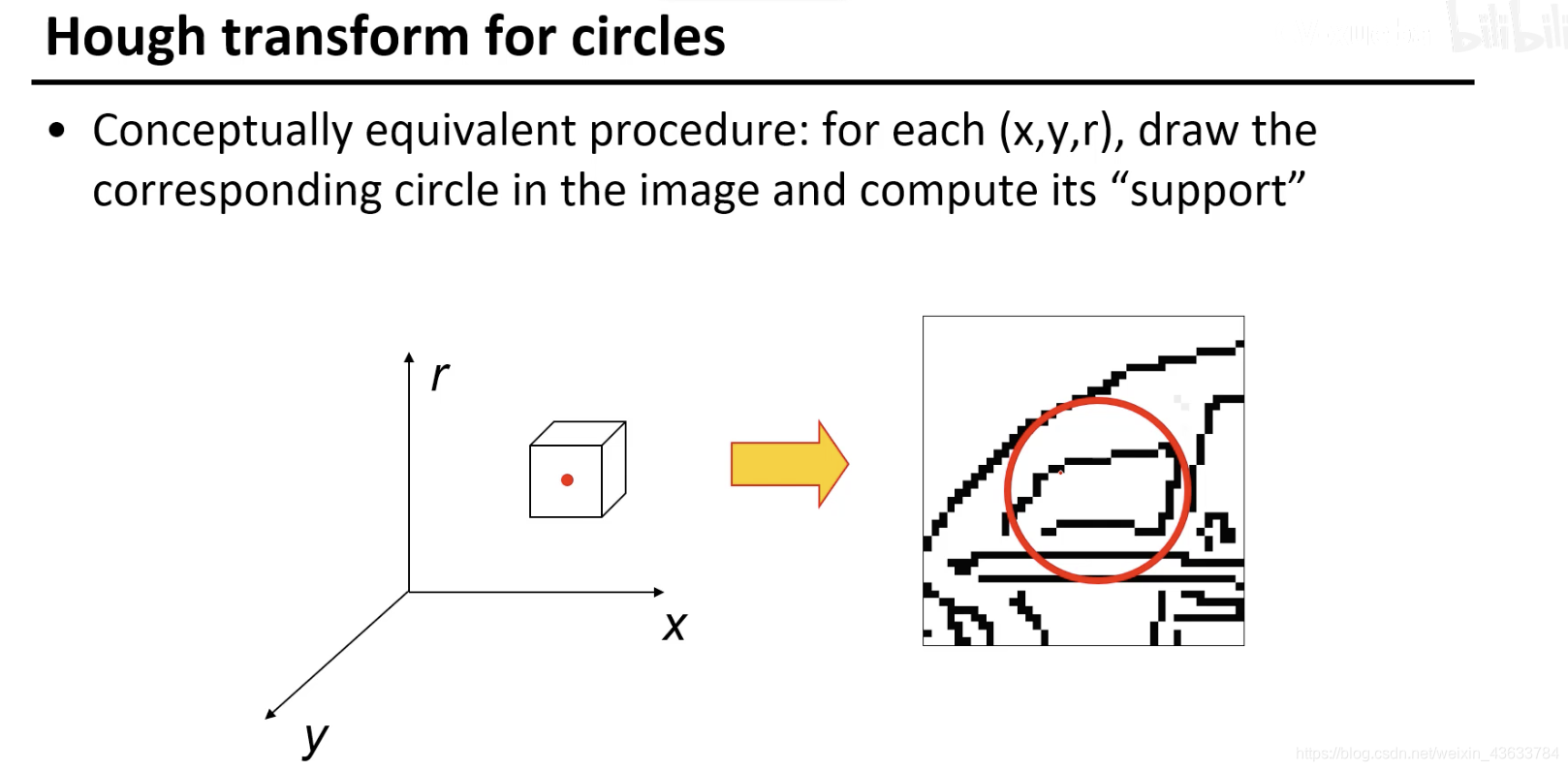
这里有两个方法：

1. 左侧空间上的每个位置给给右边的空间画一个圆，然后在右边的空间上看有多少个点在这个画出的圆上，然后根据这个这些点进行投票。不知道图像里有多少个圆，把参数空间里的每个点都在图像上画出来，变换中心，然后对应图像中的圆，有多少个点在这个圆上（效率不太高）
2. 给定图像中的边缘然后在parameter space里投票
   
   
   
   
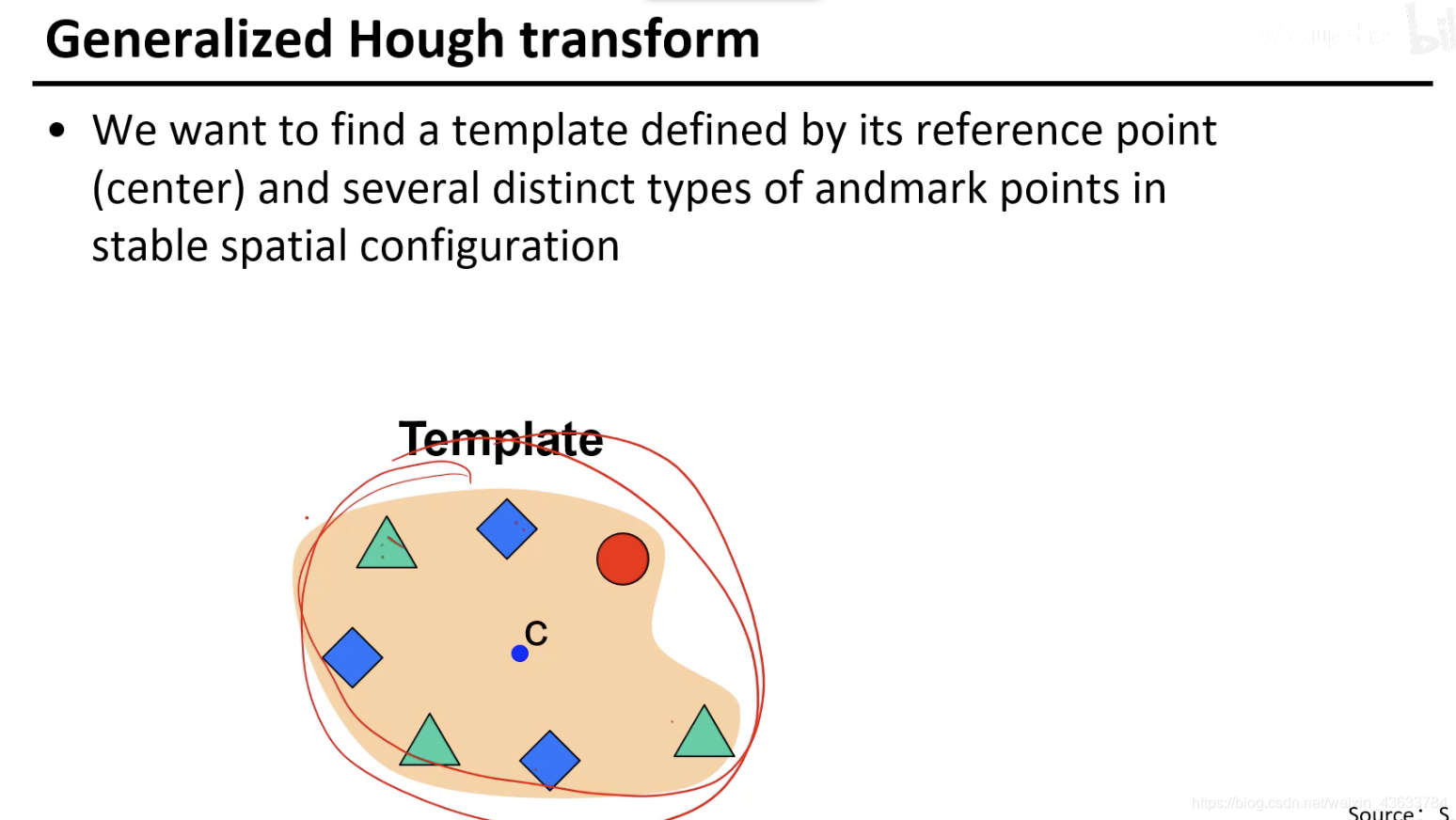
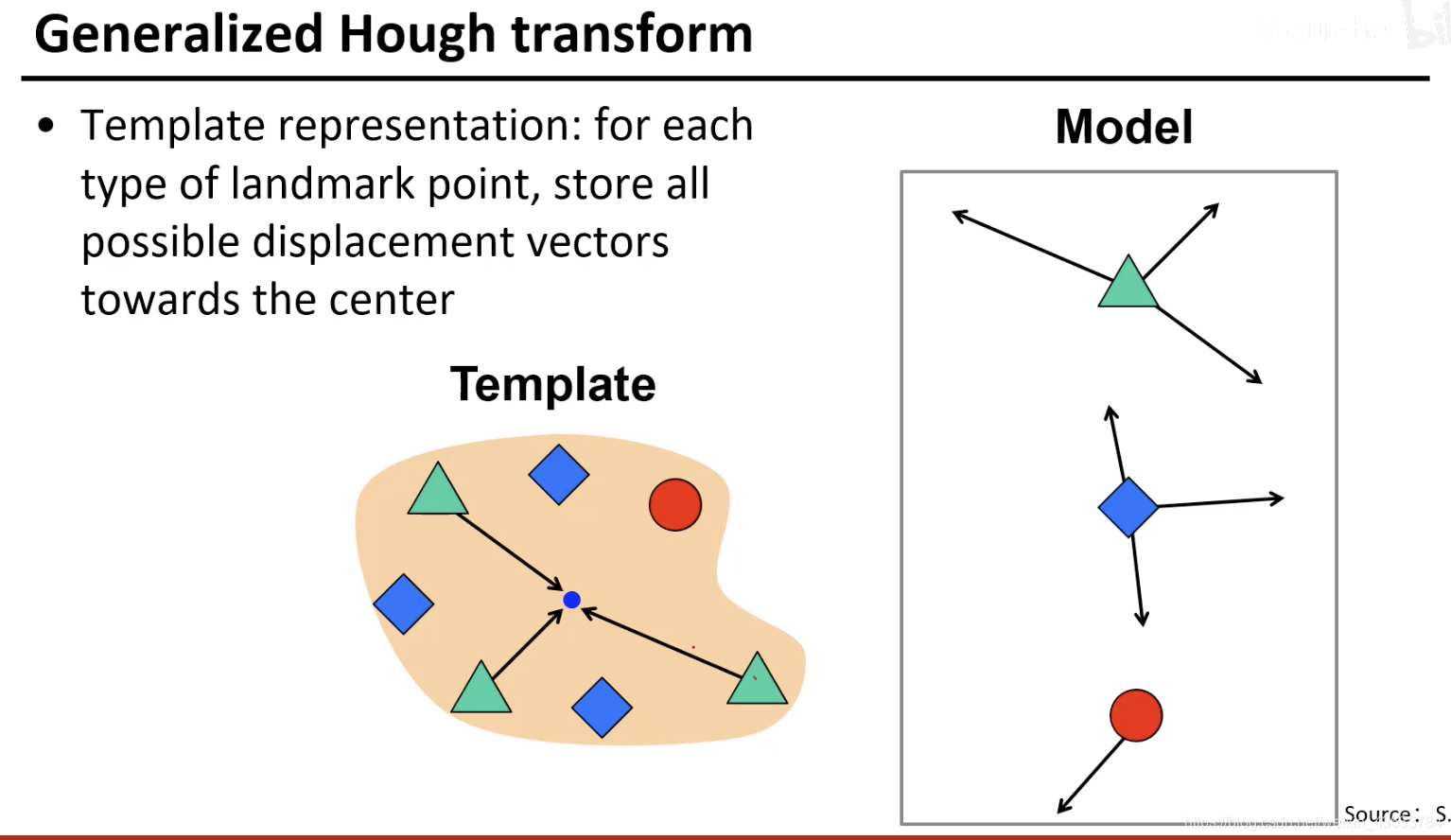
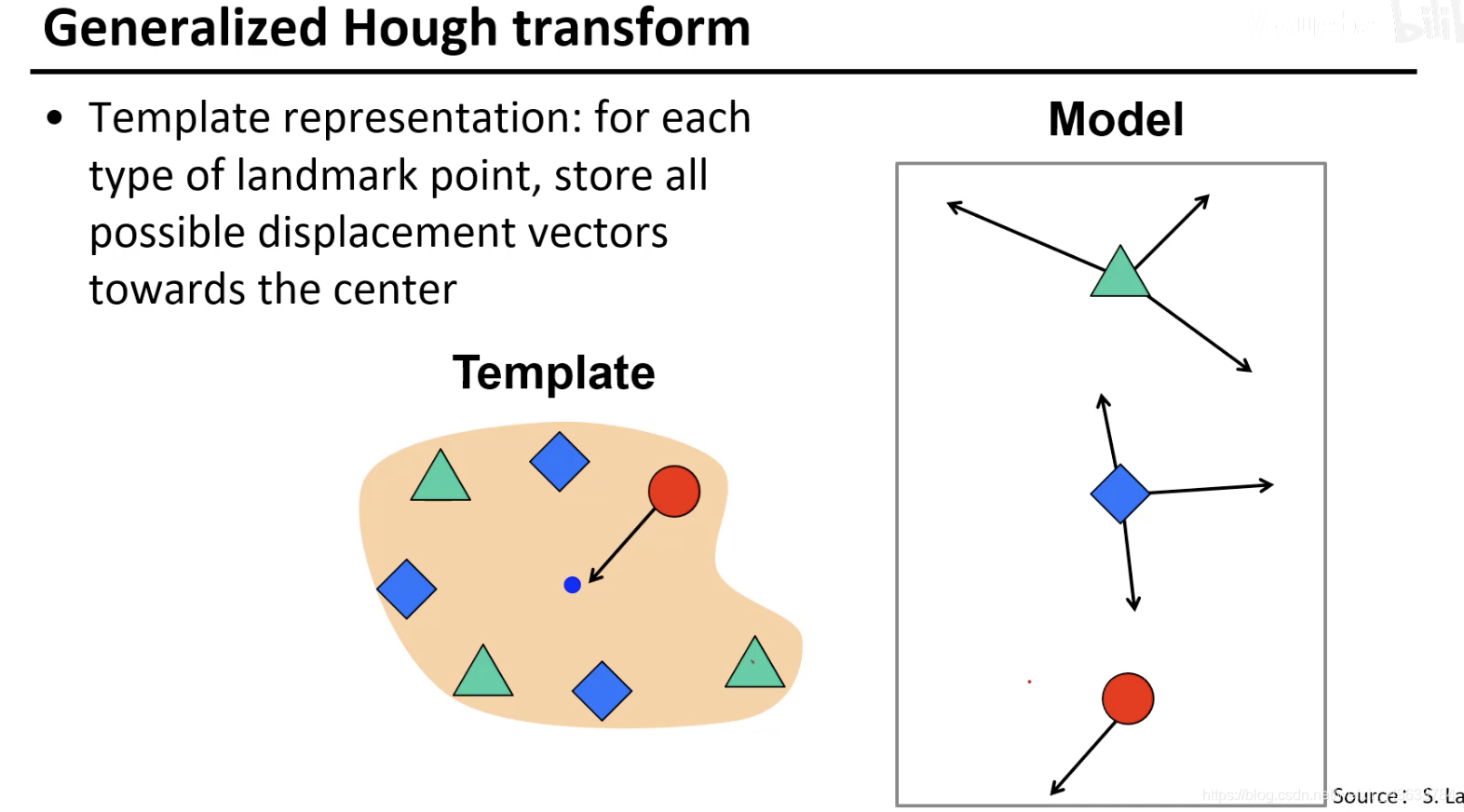
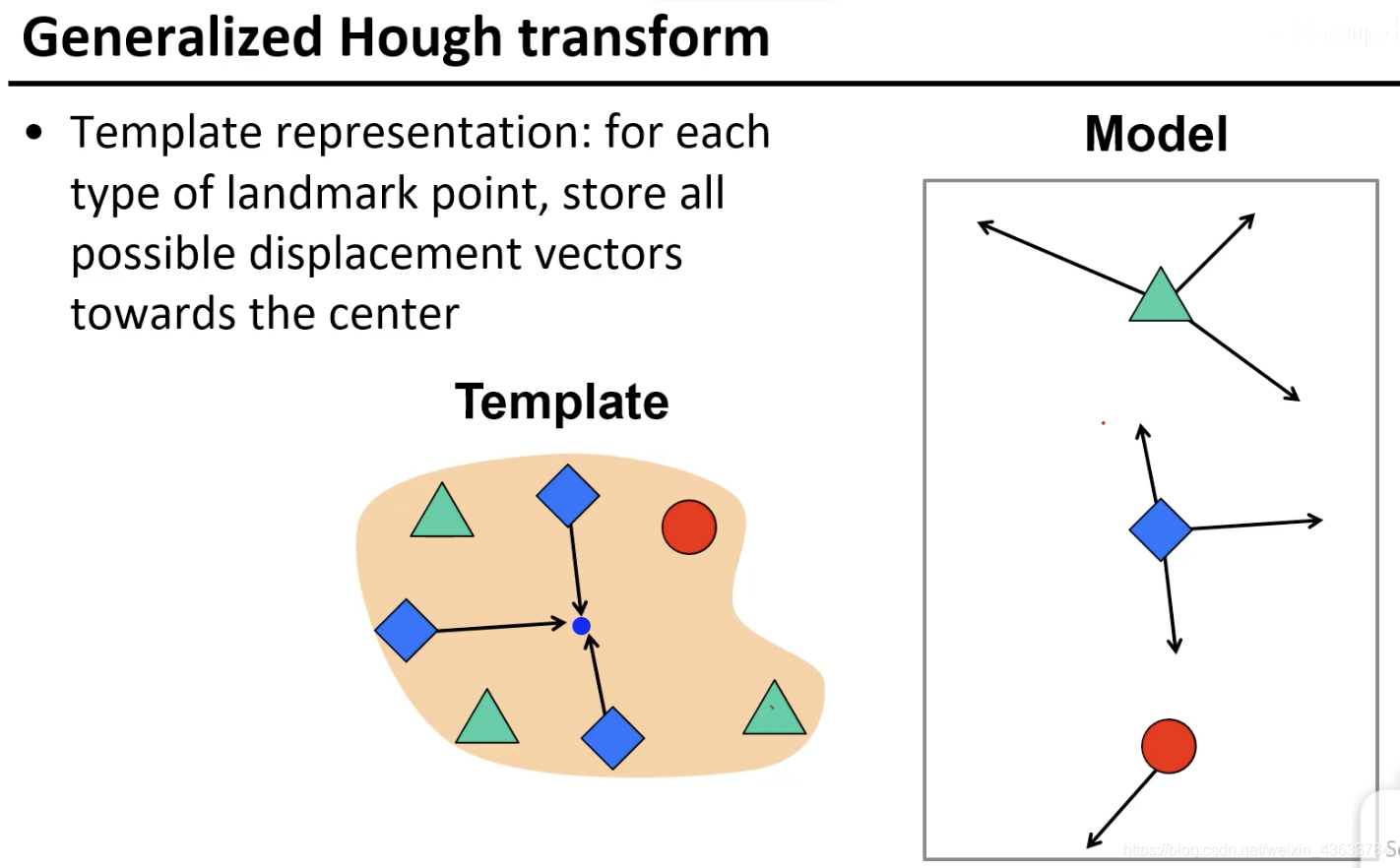
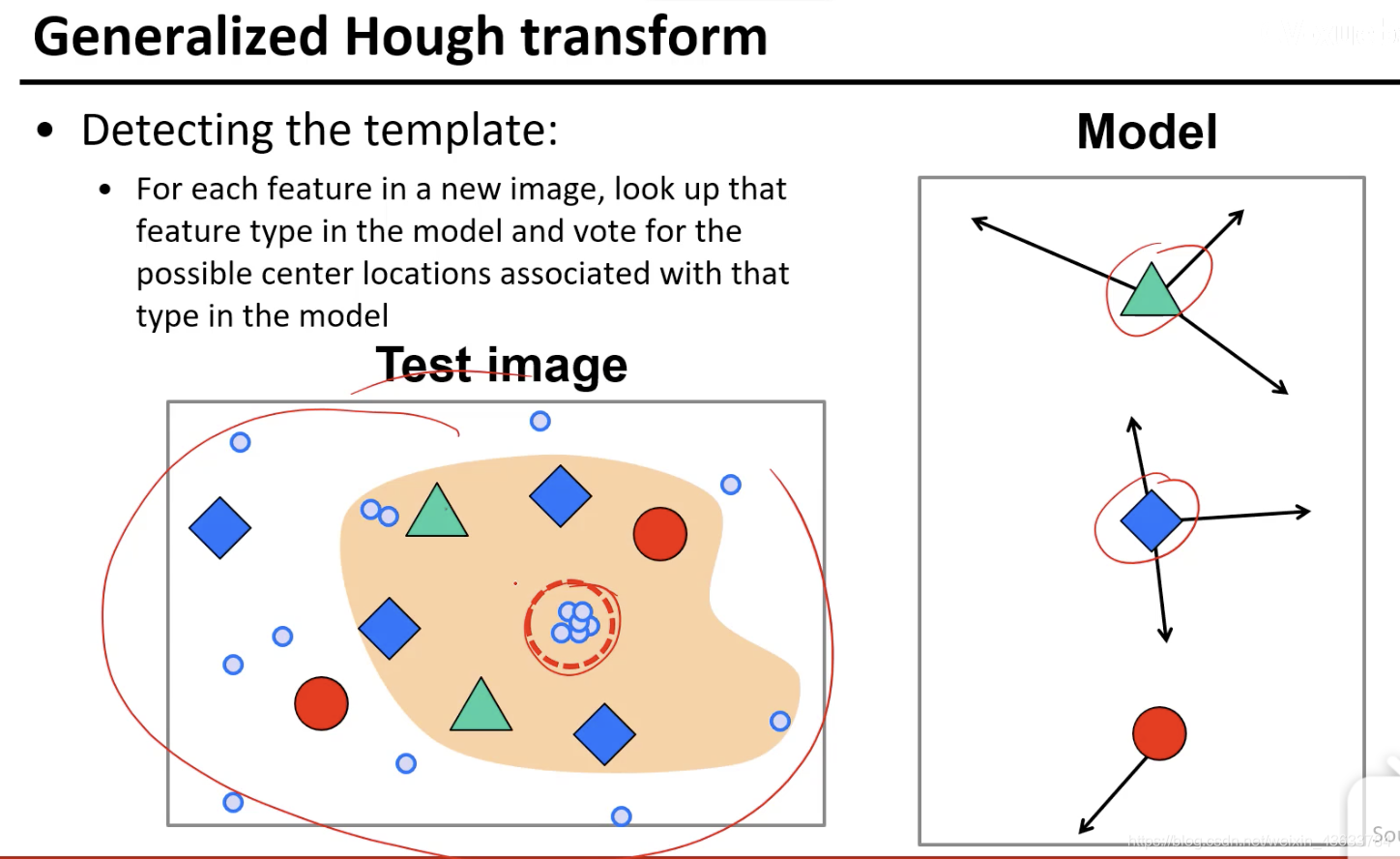
   每一种元素和中心的关系都不同，将这些不同的关系都标出来，相当于对车的图片进行了一个组合学习，就是看到Model中的每个组件的时候知道car的中心值可能的方向都在哪（图中标出的方向）
   任务：给出test image然后要找出car的中心
   
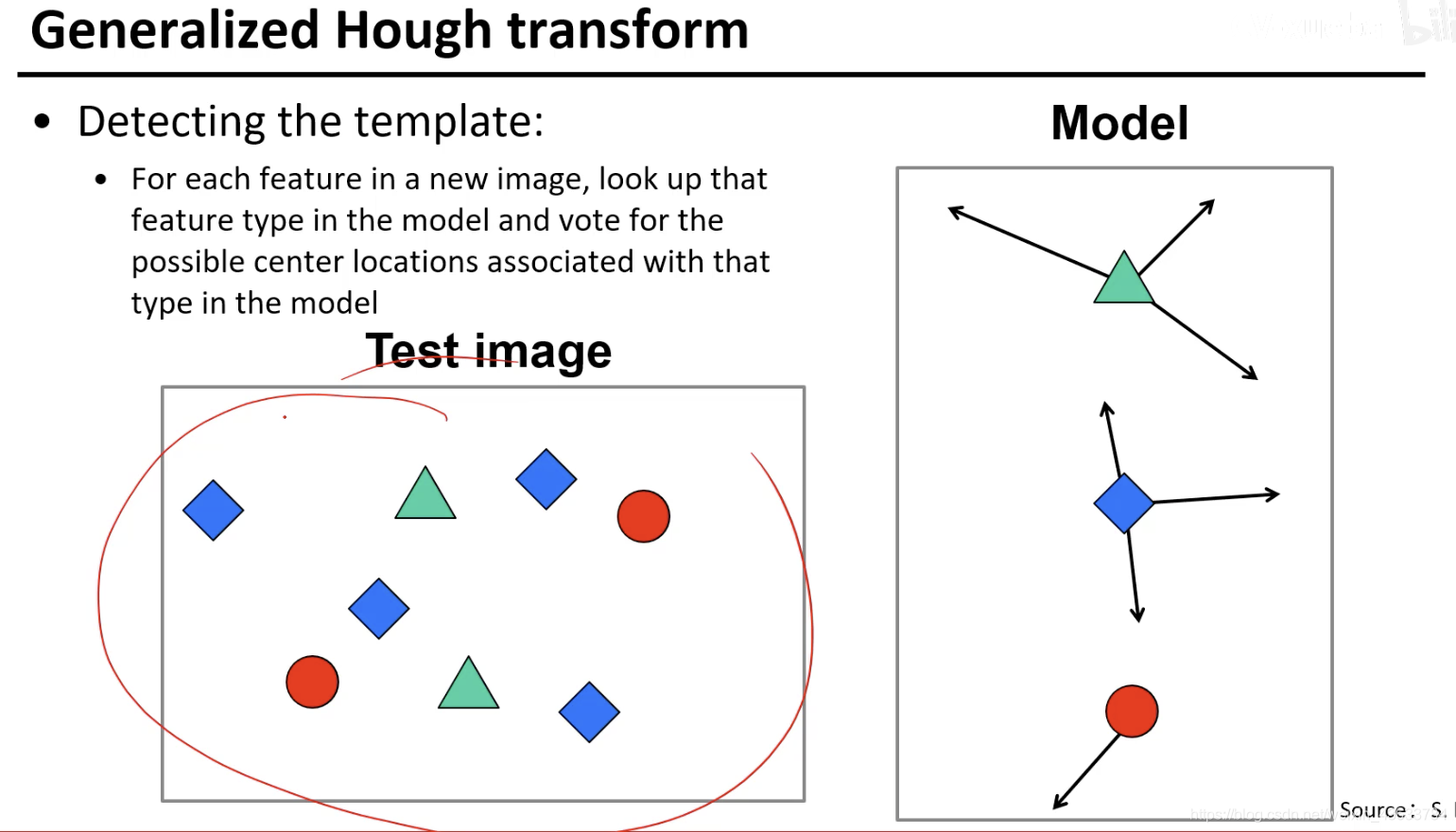
   根据每个点的中心值方向画出可能的中心点，然后对这些中心点进行投票，观察哪个中心点的票数最高。
   
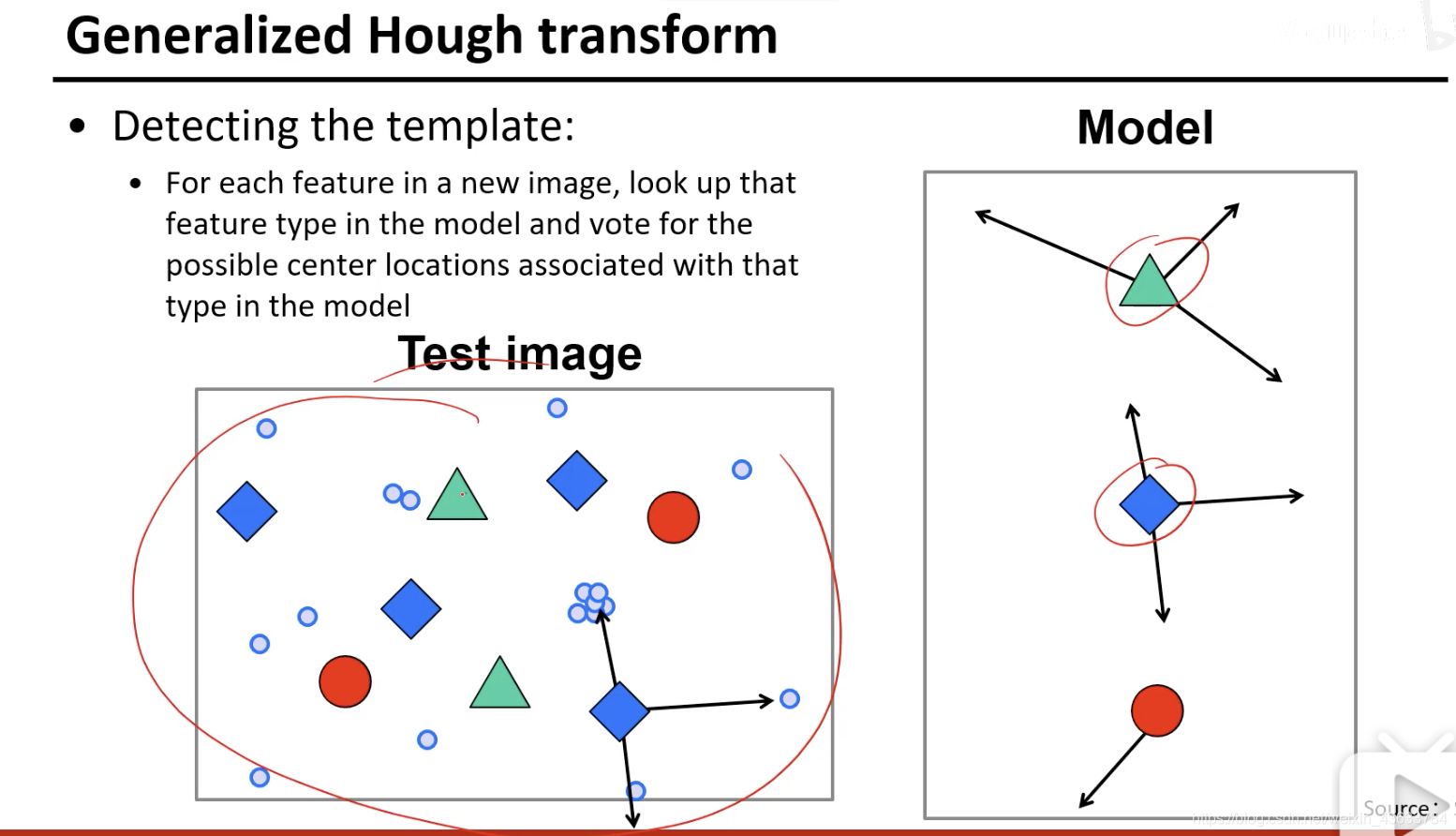
   看哪个点的票数最高，这样就确定了车的中心点，从而确定了car的位置。
   
   这就是Hough变换的一个应用。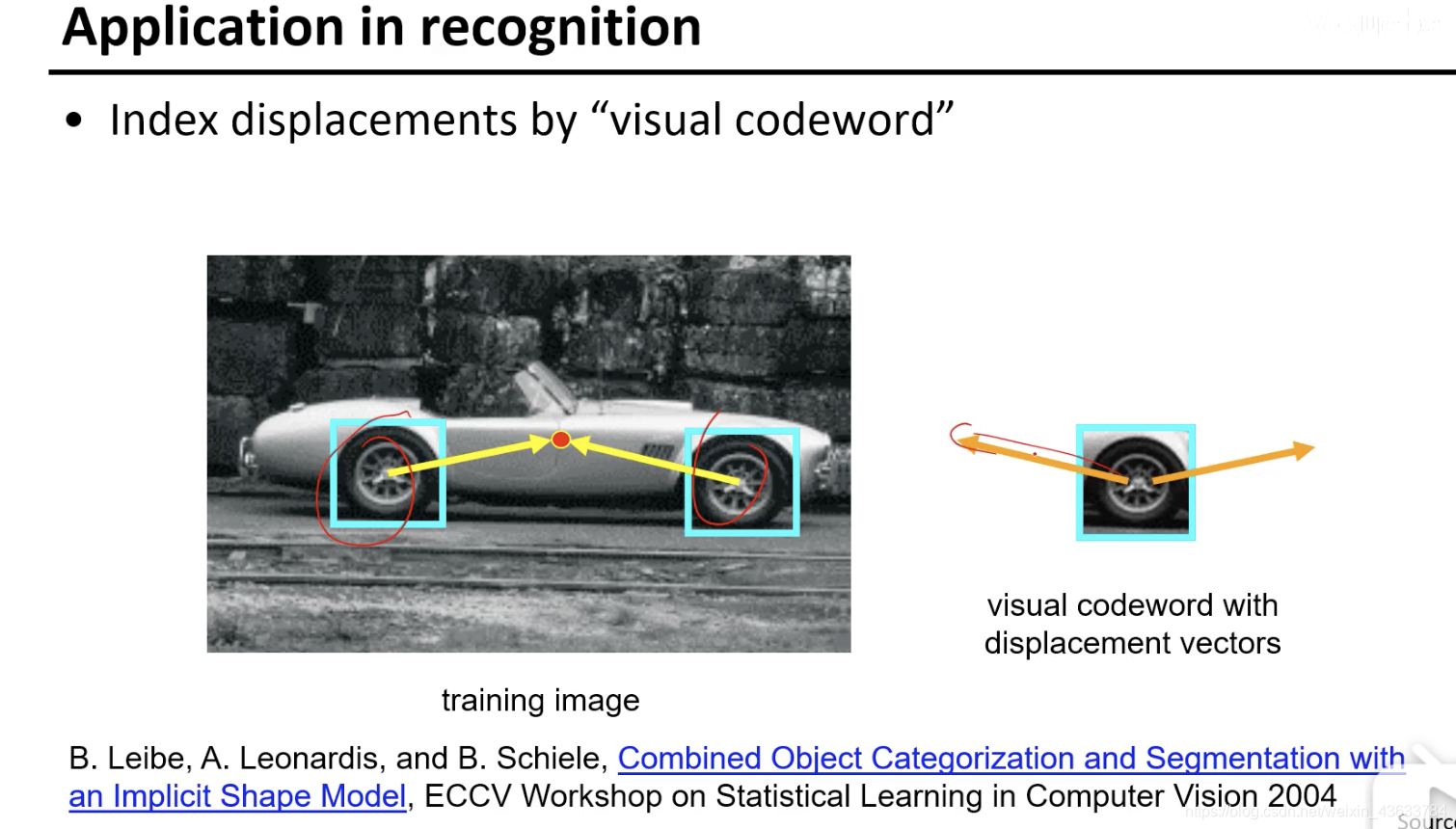
   比如上图，一开始先学习到车轮和车的中心的一般的关系，然后给定一个车轮就知道一般的中心方向在哪，将来在真实情况的 时候检测轮子，然后给中心投票就能知道车的位置在哪里。
   
   Hough变换在更多的这种配置的学习中的应用，因为很多东西是组件配置起来的，那么很多种情况研究局部组件和中心的配置关系，然后将来在真实的情况下将每个组件的中心都画出来，然后看哪个中心的投票数比较多
   ⚠️⚠️cv三大会议：
3. CVPR、ICCV
4. ECCV（欧洲的）

Hough transform的优势

1. 非局部和有遮挡都没有关系
2. 可以解决多个实例，但是有可能出现一种情况就是一个点的周围投票值都很高，就3. 会出现有一堆线大概都差不多处于一个重合的位置。【可以使用非最大化抑制的思想解决】
   噪声比较鲁棒(假设一个前提：噪声点不会给每一个格子投票）
   
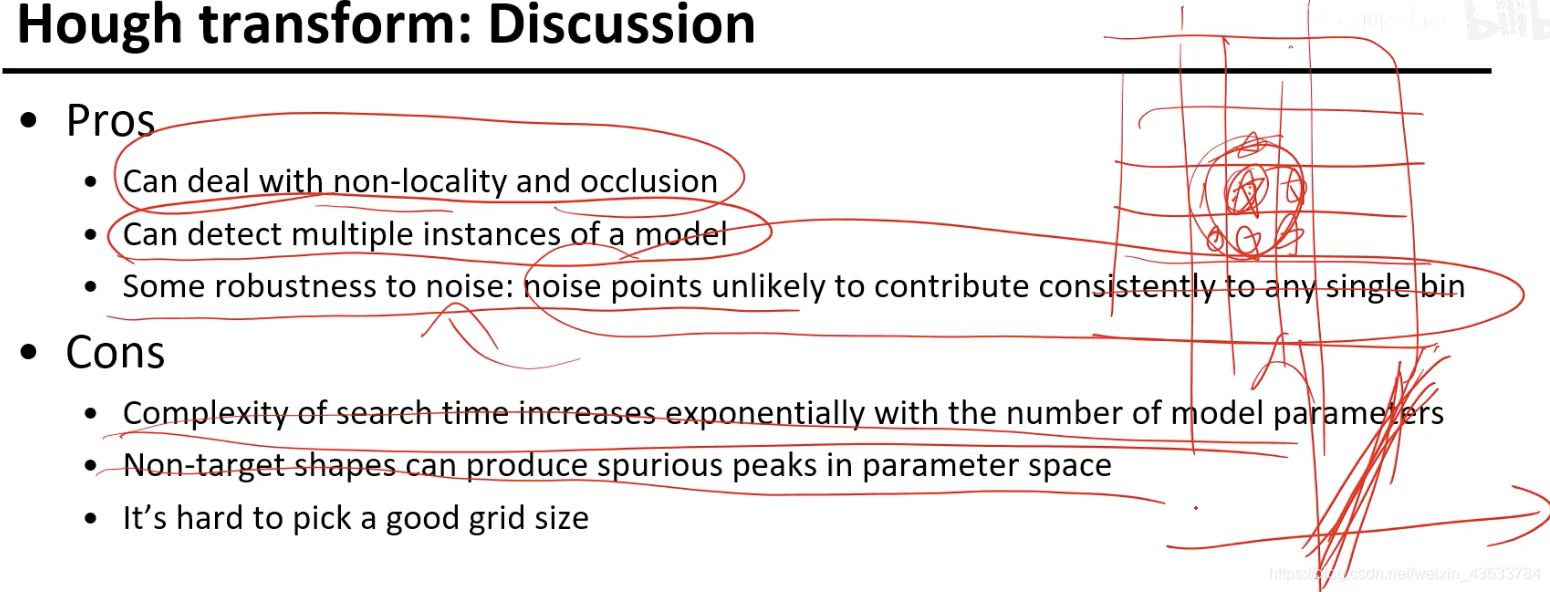
   缺点：
3. 搜索空间比较大（二维或三维相对容易，但是随着参数维度的增加就不容易了）
4. 如果没有形状的东西在参数空间形成一些伪的峰值，本来没有形状但是会拥挤到某几个空间内进行投票产生伪峰的话，也会把最大值输出来
5. 离散化，离散化过大精度变弱，过小超过门限（软投票解决，一般都会增加这件事的性能）

Hough transform vs RANSAC

RANSAC只能输出一条线，但是也可以多条线，相当于要记录多个最大值，最后用投票数进行输出，但是有一件比较麻烦的事：外点多的时候N的次数就很多==？？？==
Hough tranform对参数空间影响就比较大，就是在多维空间的时候处理的不好，还是得用RANSAC

Local features（局部特征）

全景图像拼接

如何实现panorama stitching？

1. 提取特征（特征检测，检测左图的时候不知道右图的存在，检测右图时也是）
2. 匹配特征（找到对应点，左右图像的类别信息即可匹配），通过匹配关系找旋转和平移矩阵
3. 经过旋转平移矩阵的变换把相同的地方连接起来（对齐）

定义好的特征点的原则

• 左侧检测到的点右侧也要检测到，具有重复性，重复的点越多性能越好
• 选择具有特点的特征，有代表性、显著性，能找到对应关系
• 计算特征比较高效
• 计算的时候只跟小局部有关系

特征点检测

机器人导航会应用到三维重建。

角点

比如书角，桌子角，不找直线上的点，直线上的点是不稳定的，对应不了，这样对齐关系就很难，不满足显著性。角点区分性很强。
两个方向变化最大的点（角点）

角点识别

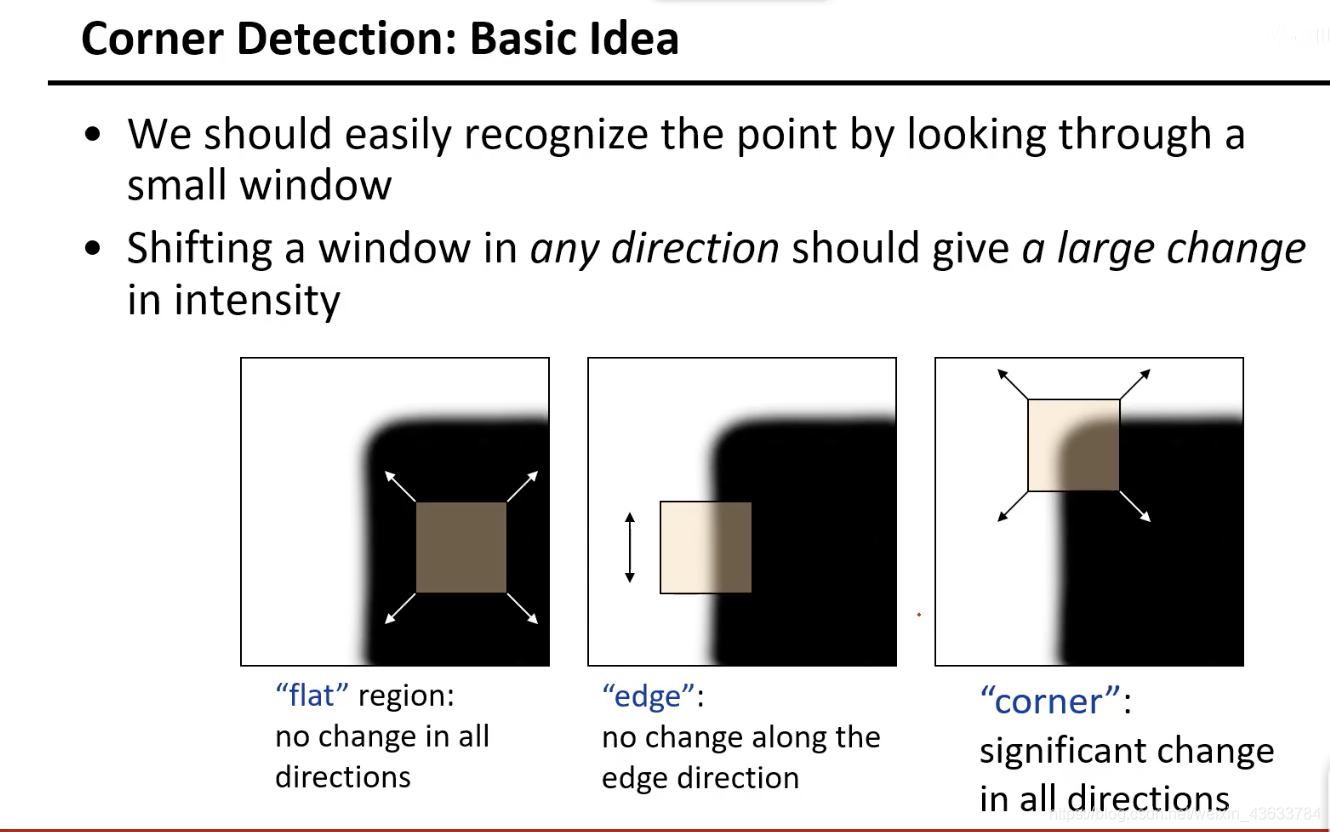
在没有角点的区域里移动是没有影响的，平面上的点如何移动都不会改变；第二个图沿着上下方向移动也不变，但是左右移动是会改变的，所以是有一个方向上改变另一个方向上不改变；第三个图沿着每一个方向移动都会变化。
现在给出一个通俗的定义就是至少在两个方向上发生改变的点即为角点。

E(u,v)就是两个框框里面的差异，反映了移动（u，v）向量的时候原图像和变换后的图像的差异。（1. 怎么挪( u，v)2.挪完之后的差异E(u,v)）
想知道(u,v)变化和E(u,v)变化的关系

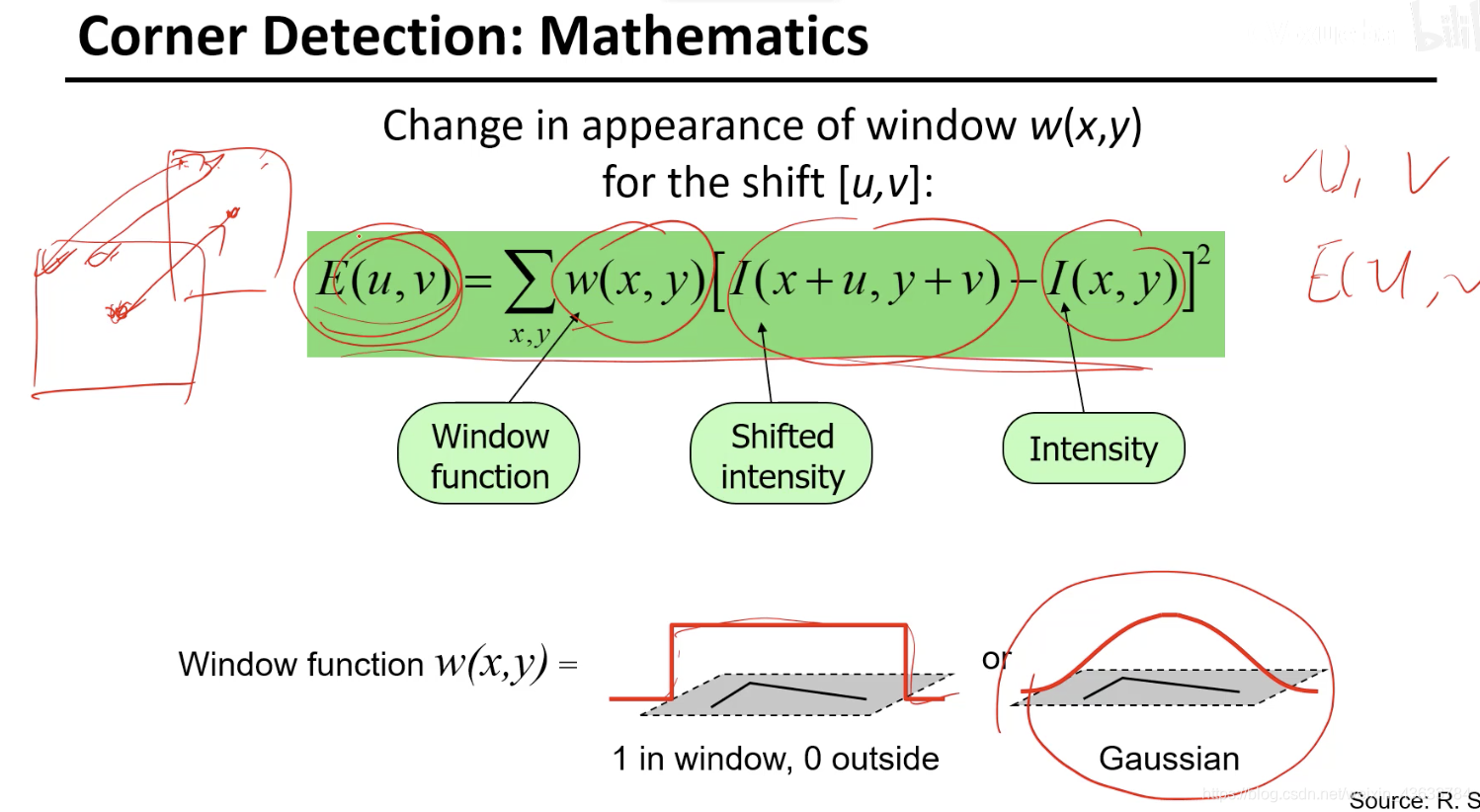
w函数评估每个点的差异值对当前判断是否为角点的点的贡献。1：不考虑每个点的重要性差异，重要性都相同。Gaussian：离角点越近对差异求值贡献越大。

在计算的时候这个公式需要取像素来计算二者的联系，但是想要直接判断，所以使用泰勒展开计算。

如何不通过分析每个像素直接找到E(u,v)和（u,v)的关系呢？（因为如果直接根据（u，v）去找点的话x，y每次都要取一对像素值代入才能够找到对应的E(u,v)但是这个过程过于繁琐。
使用泰勒展开式，在u=0，v=0的点展开（二维），这样(u,v)的变化直接就可以建立和E(u,v)的关系。

推导结果：（复合函数求导然后把（0，0）代入）

在这里把上面的函数就当成是连续的函数进行求解，不考虑离散，但是在计算Ix的时候从图像的角度再去看，因为直接求不好求。最后整理成如下的形式：

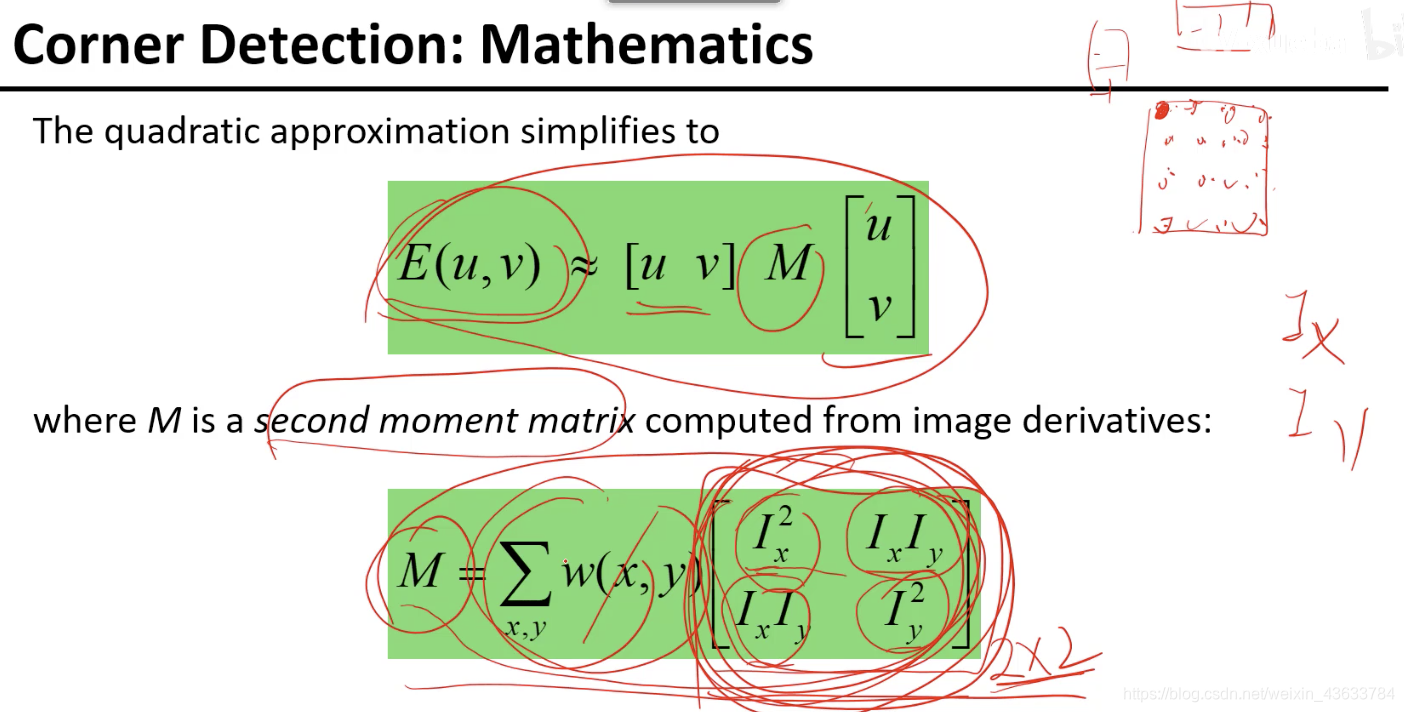
• 每个点的二阶局矩阵加权求和得到的，M也是一个2x2的矩阵。在一个小区域里是可以将M求出来的，导数可以用[1,-1]和[1,-1]^T来进行xy两个方向卷积得出，然后在当前区域里每一个像素点都可以进行先按照上式卷积然后构造出那个2x2的矩阵，然后再对每个矩阵进行求和。
• 类似于y=ax+b，在E(u,v)和(u,v)关系中，起决定作用的是M矩阵，所以通过这个矩阵就可以分析二者之间的关系。
  
  
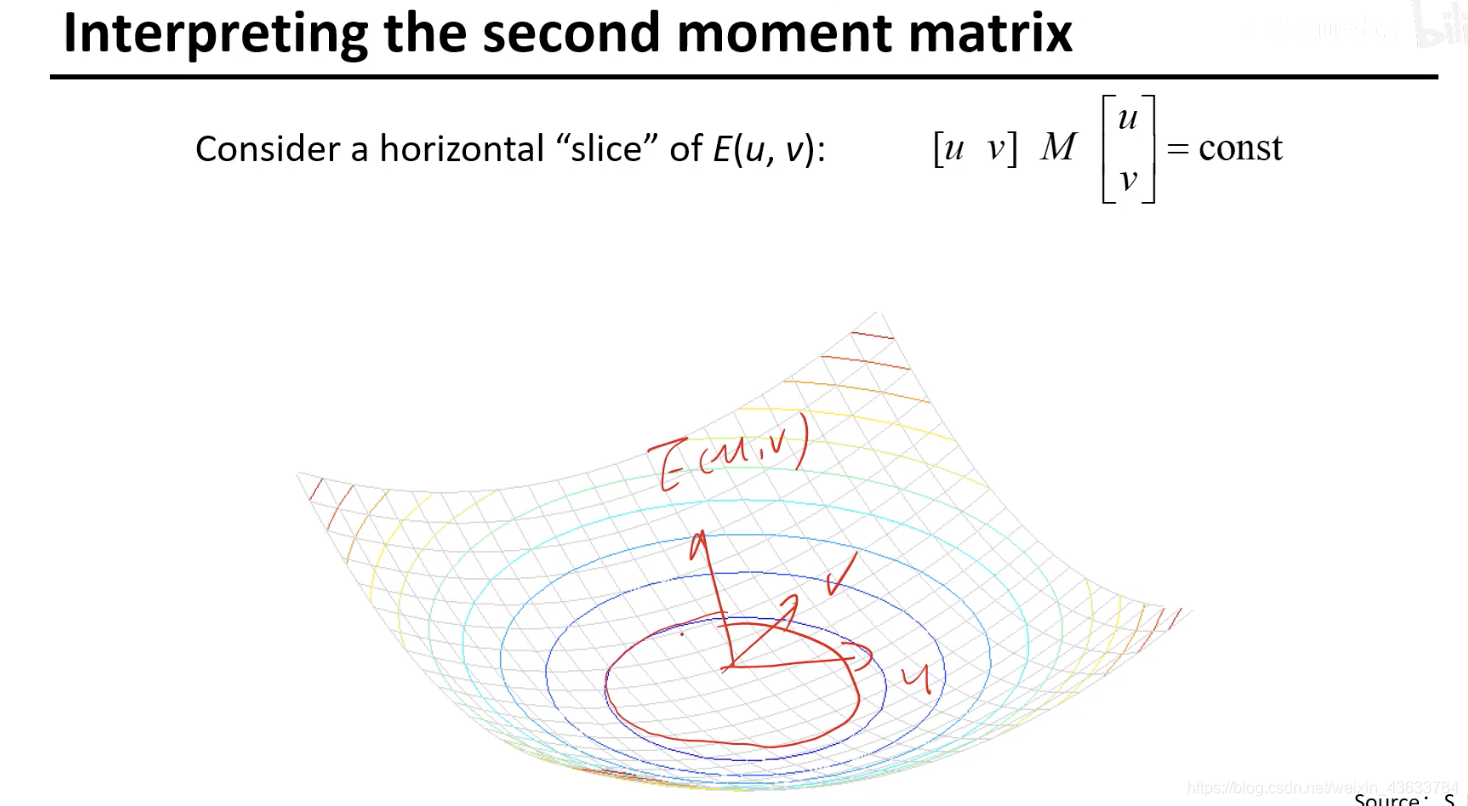
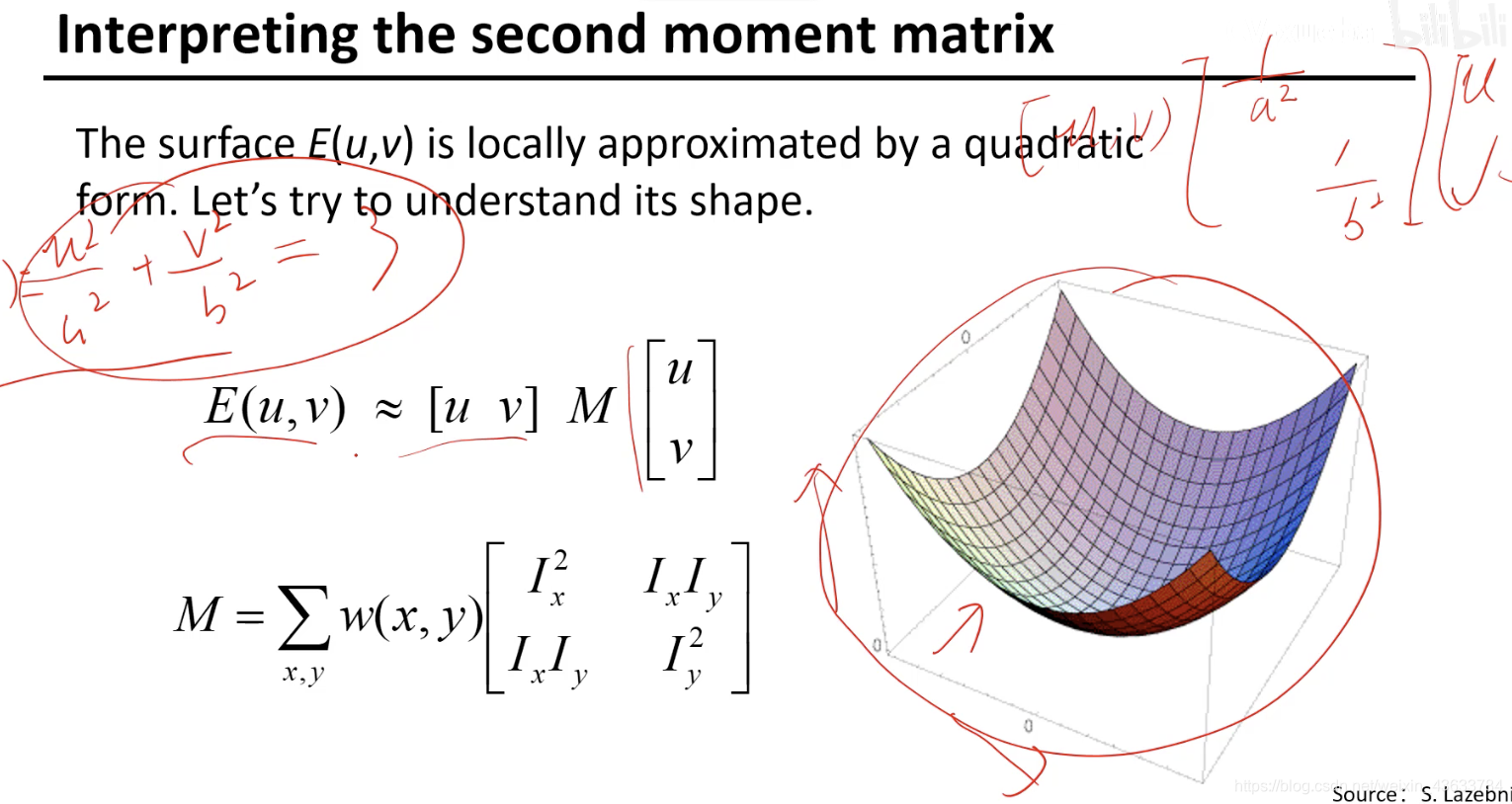
  给一个E(u,v)的值对应一个椭圆（如果是一个一个数值的话）
  
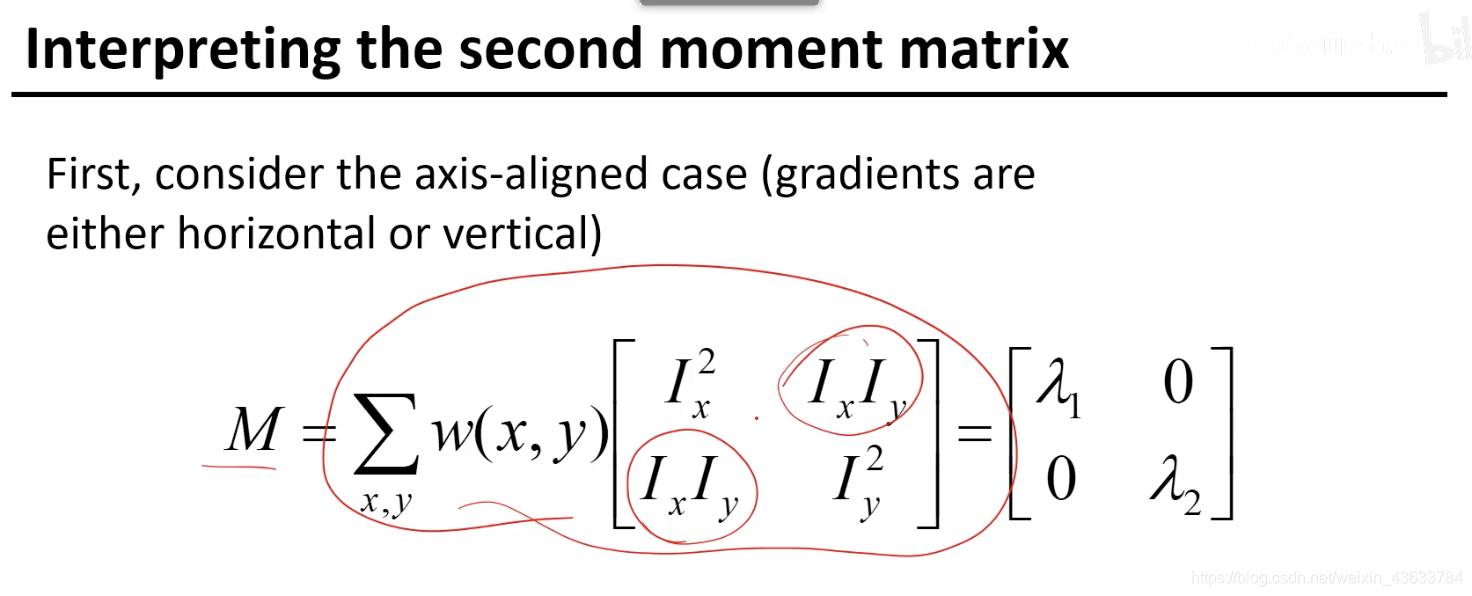
  假设Ix和Iy是互不影响的，假设二者是正好垂直的，
  
  
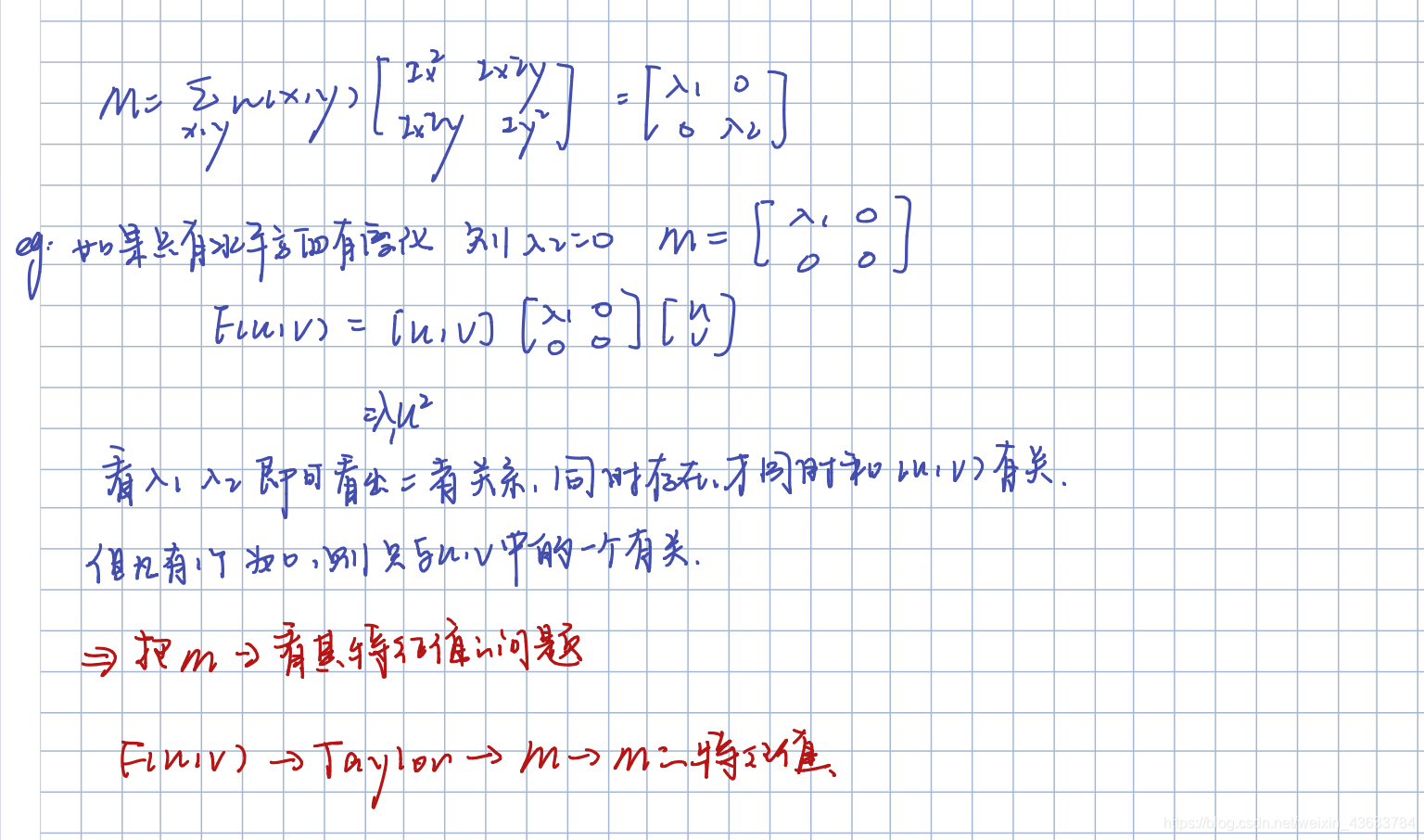
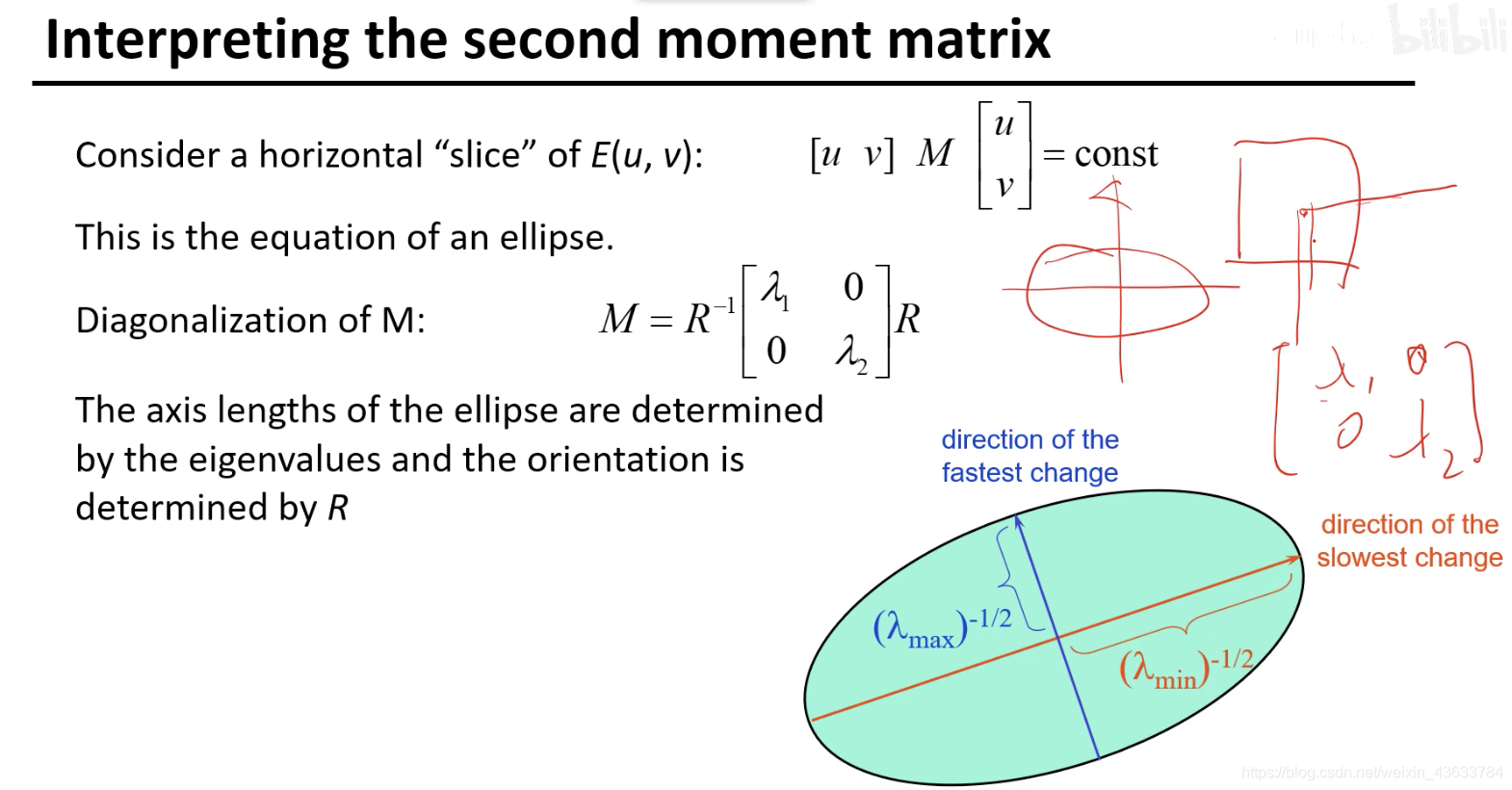
  现在如果M矩阵不是对角矩阵而是一个普通的实对称矩阵，这个时候如何处理？
  将其分解，分解成对角矩阵和初等矩阵的乘积形式。
  旋转矩阵的逆等于其转置
  R如果是单位矩阵的话，椭圆就是正的，没有变化，如果R不是单位矩阵，椭圆会有一定角度的旋转，如果想要旋转椭圆到一定的角度，就将单位矩阵替换掉。

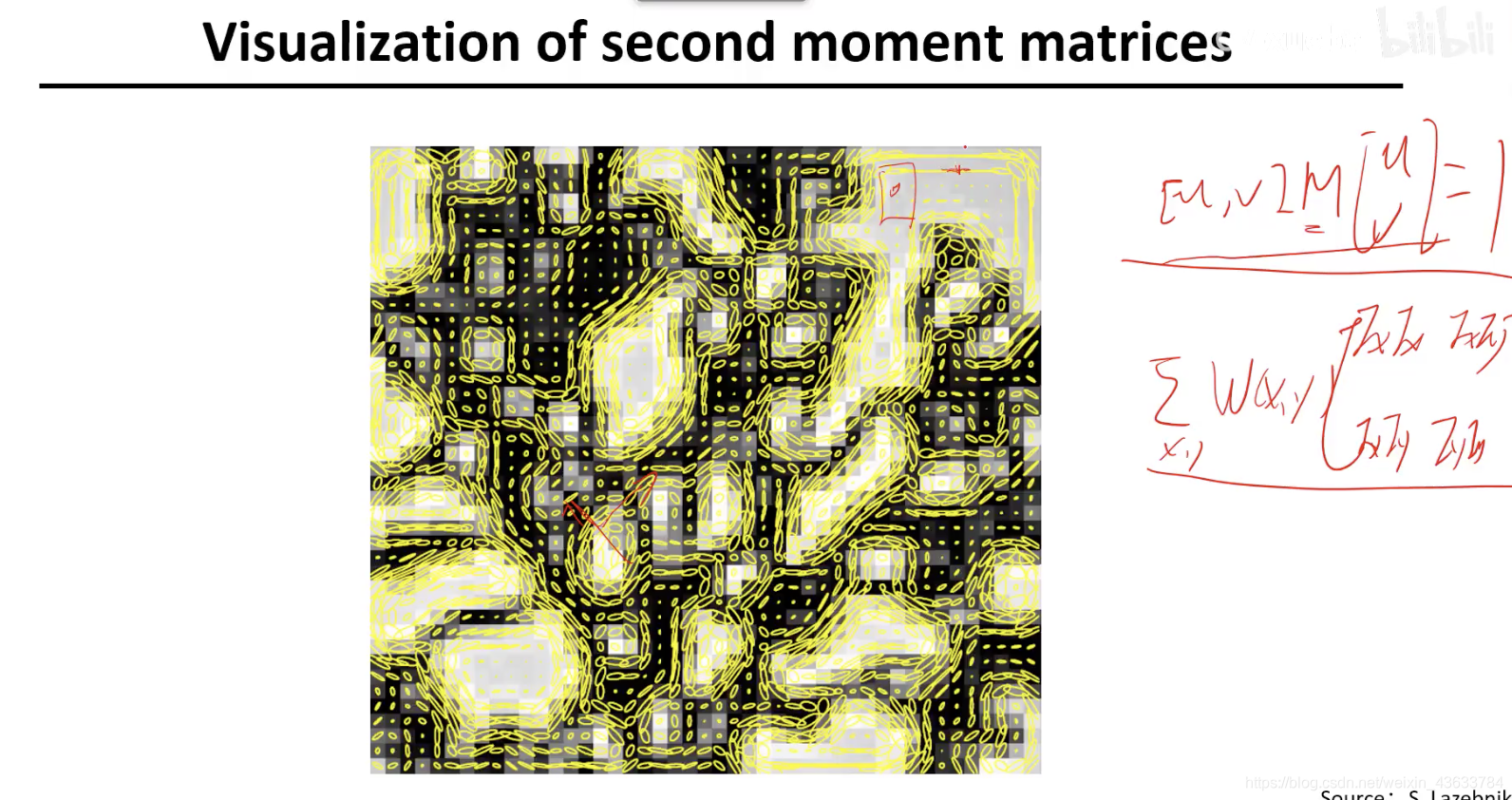
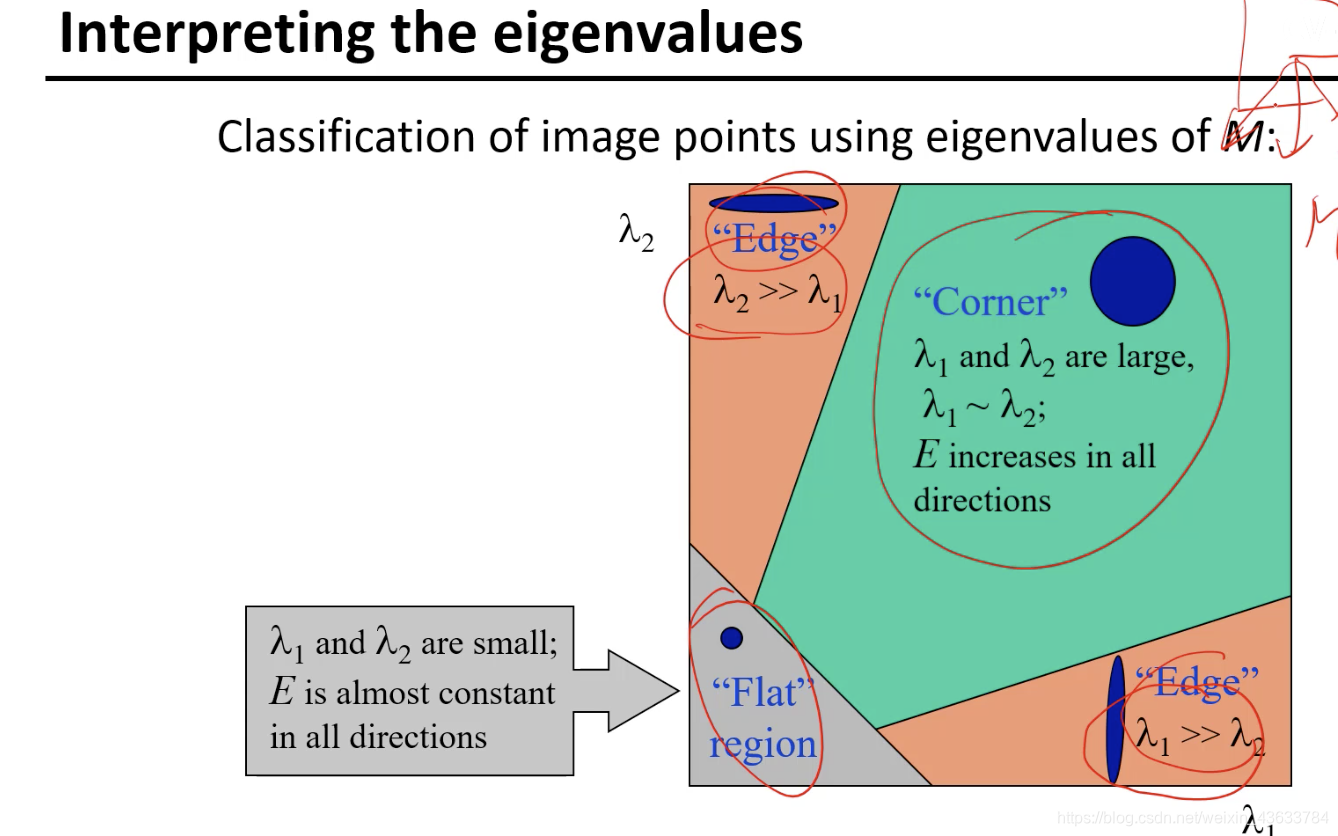
到边界的地方容易某个方向基本为0，为短线的形式，在另一个方向上变换的较快，因为二者差异大，lambda较大，分母大整个数值趋于0
平坦区域lambda1和2都很小，就类似于一个点。
因为lambda1和lambda2是从最开始的(u,v)->E(u,v)关系的一个表述，也就是两个区域被移动的变换的表示，所以lambda1和lambda2的大小代表了变化的大小也就是可以理解为两个方向的梯度变化，lambda越大的变化的越大，lambda越小的变化的越快，但是表现在椭圆上是lambda小的轴长，lambda大的轴短。如果两个方向都变化的很快的话那么这个点是角点，如果只有其中一个变换的较快，这个是边，如果都不变是平滑区。

因为对每一个lambda进行门限限制比较麻烦，所以把两个lambda综合到一个表达式中，可以直接通过分析下式的R值就可以分析结果：

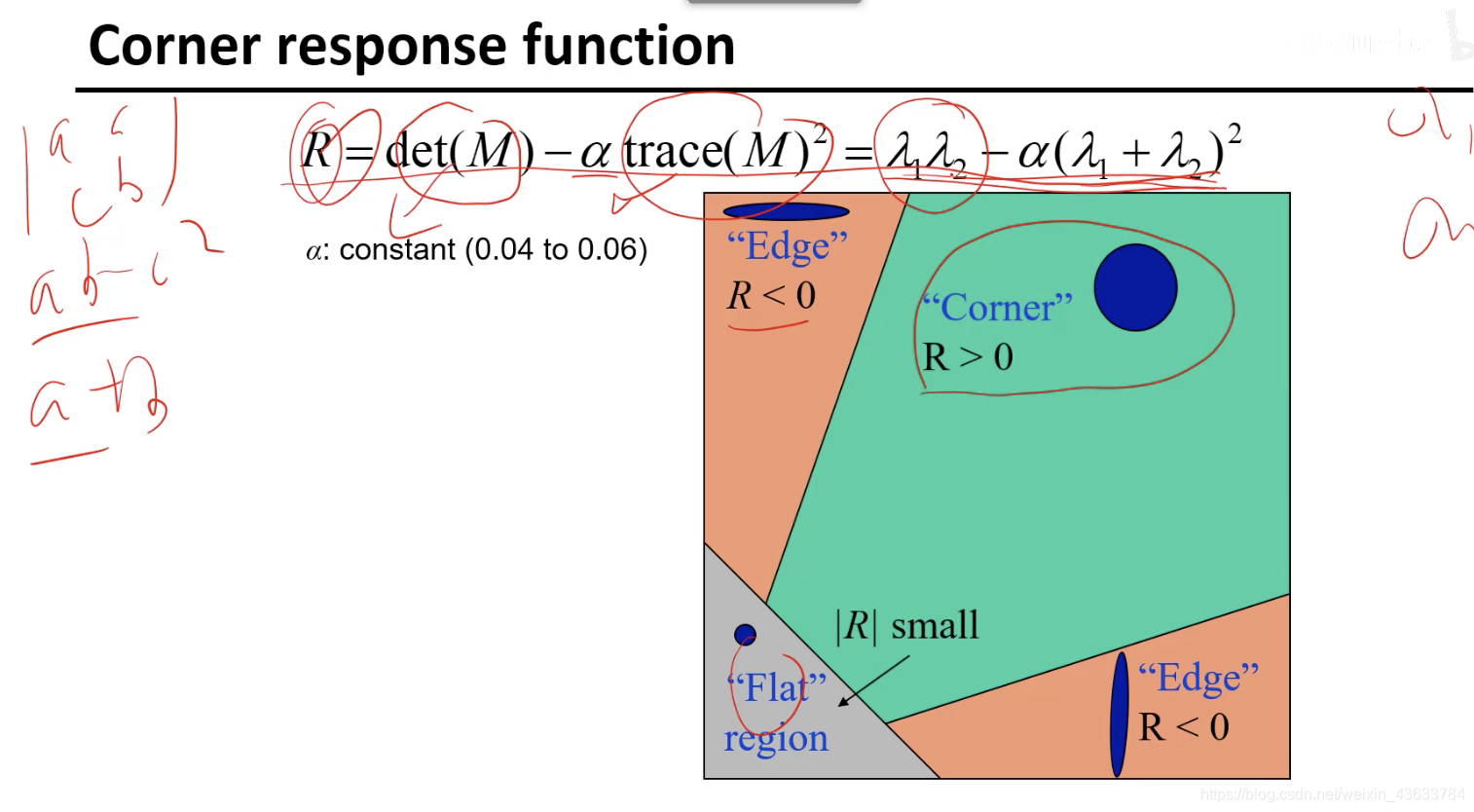
1. 用Gaussian计算导数
2. 二阶局矩阵求和
3. 计算R值
4. 当R的值大于某个门限的时候，认为是可能的角点
5. 非最大化抑制，因为在周围可能有很多干扰点
   

实例

特征提取的结果：

门限化：

非最大化抑制：提取到了相应点

Hories角点的特性

Invariance and covariance

• Invariance:
  一个好的特征提取器，对图像进行光照变换角度变换等变换之后和我原来图像提取到的特征是相等的。
• covariance:
  直接不相等，再经过一个变换之后二者才相等
  还有一些无论怎么变换都不等，那些点就没啥用了。
  
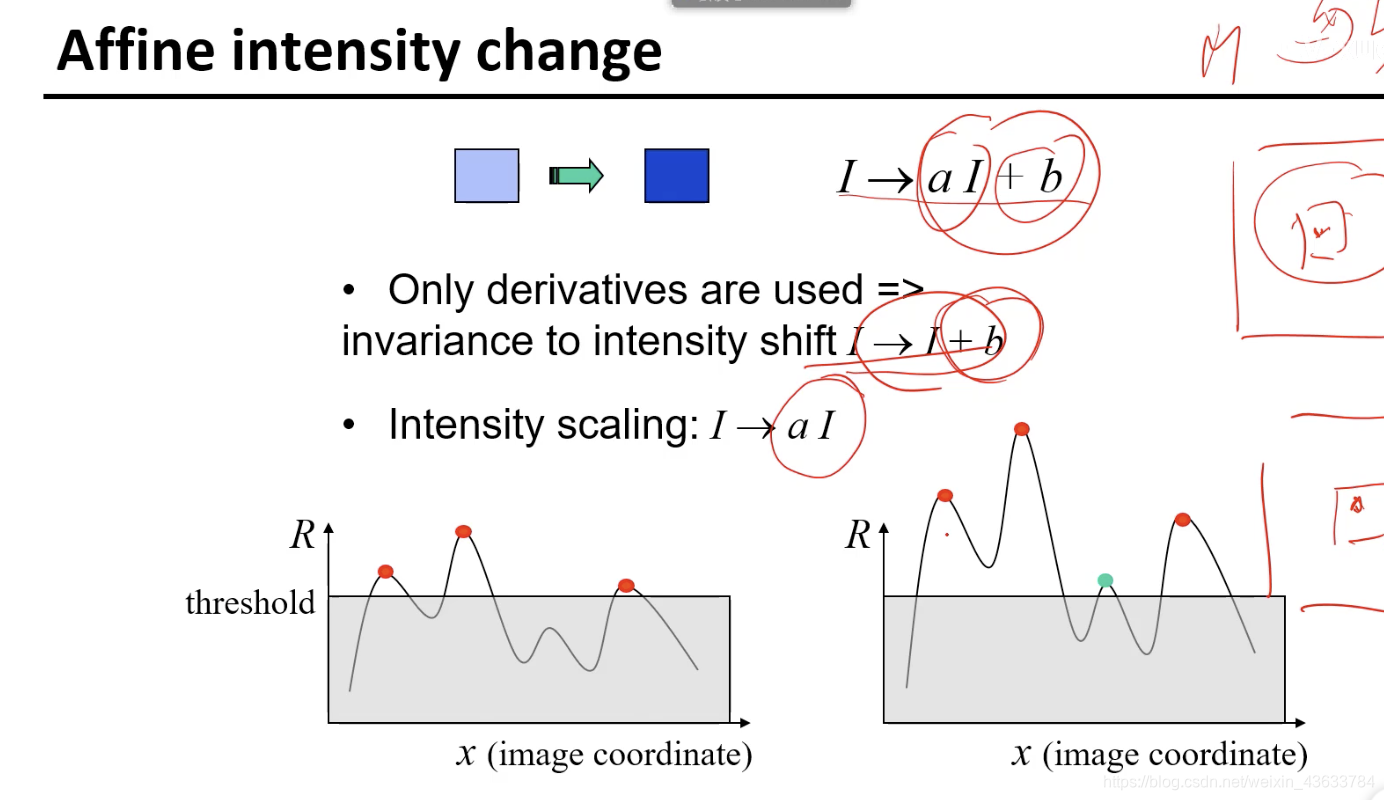
  部分的invariant可以检测出来。有些值原来没有超过门限但是在变换之后超过了门限。
  
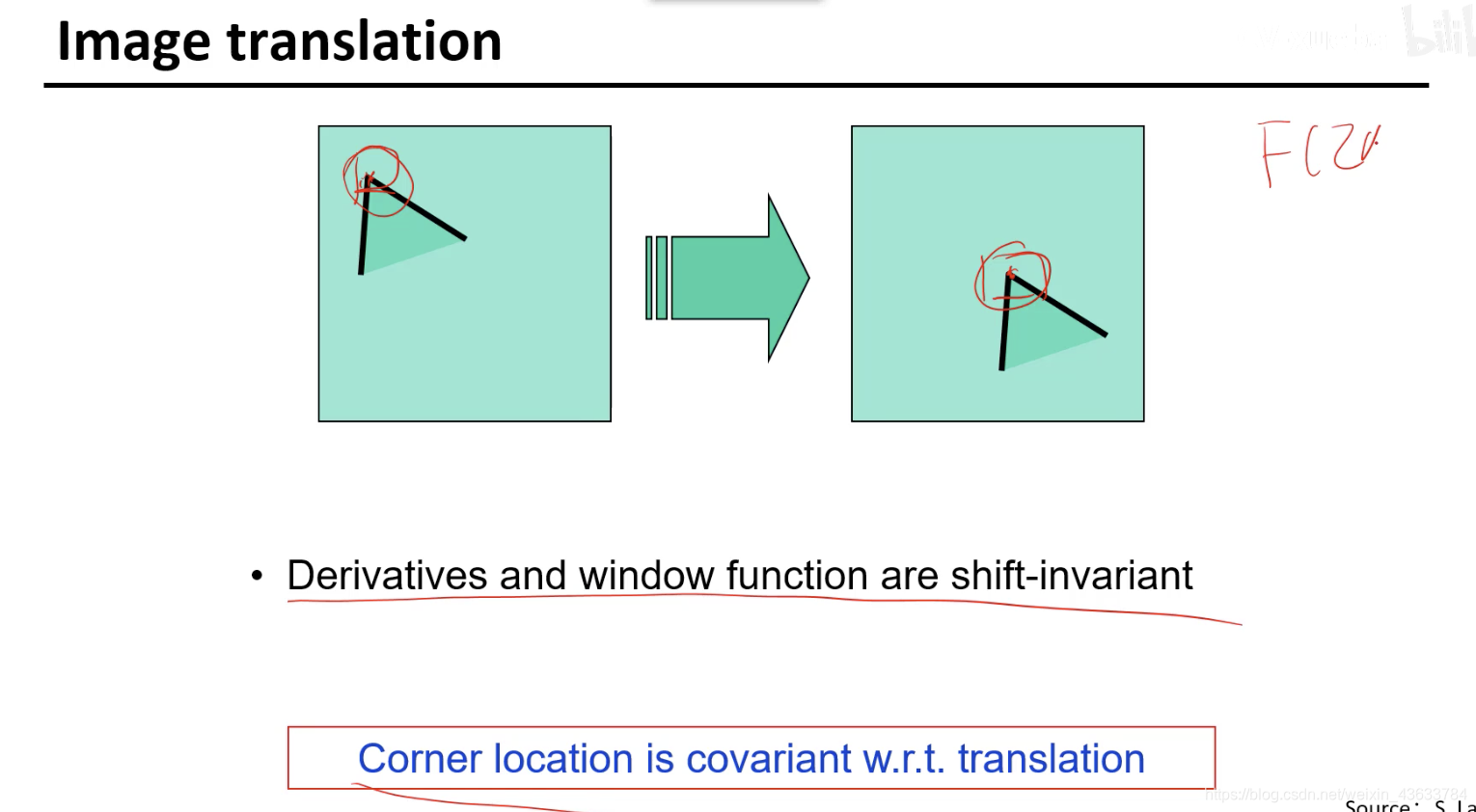
  可以加一个平移矩阵，就可以让二者一样（平移）

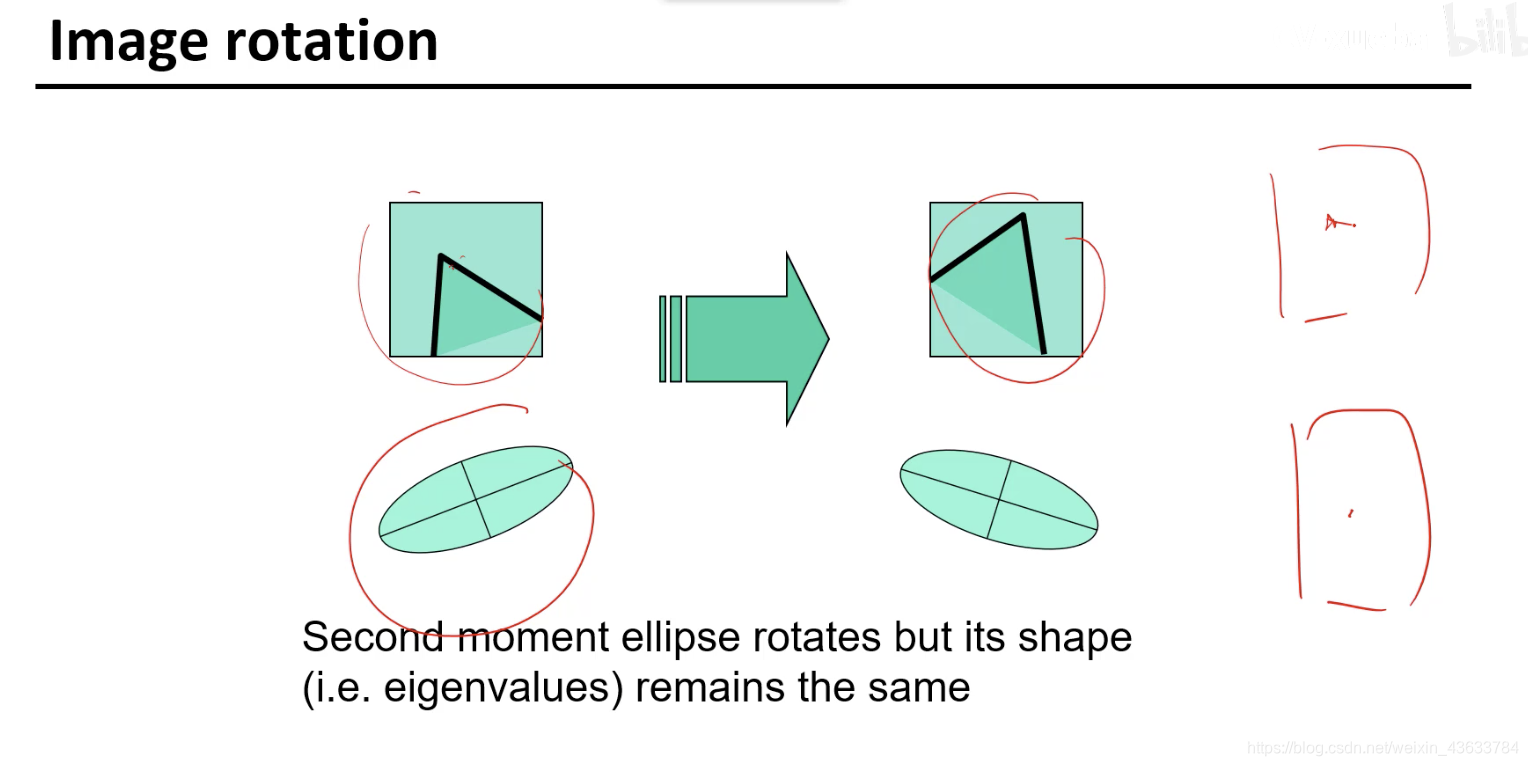
这个点肯定是能找到的，但是得经过一定的旋转才能配上。（旋转）

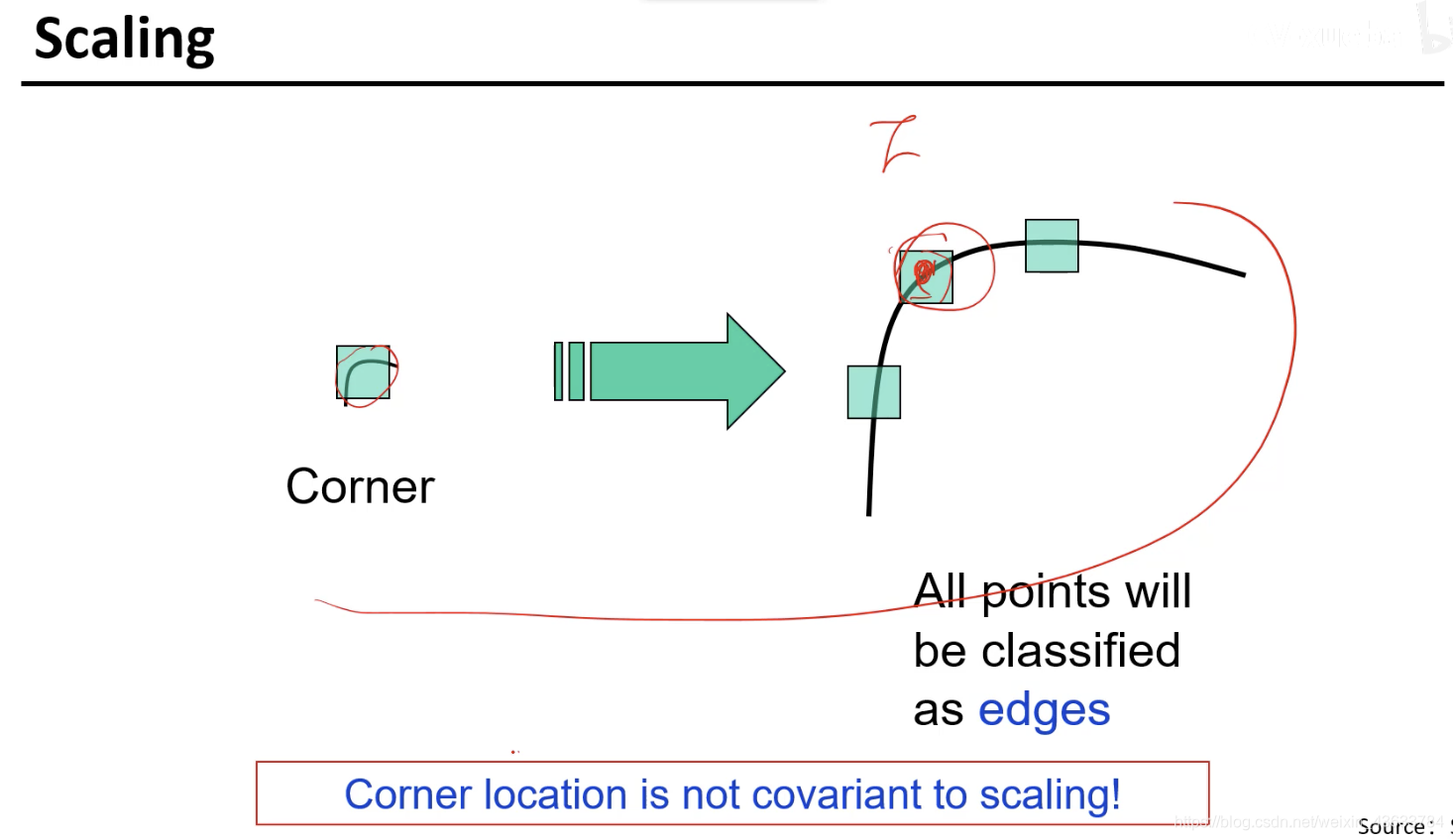
尺度变了就不行了，不具备尺度不变性，应用场景中有忽远忽近的场景就不能进行识别了。