用Turtle实现狗追兔子的建模仿真

问题背景

该案例中，巢穴在兔子正南60米处，即兔子始终向正南方向做匀速直线运动；狗在兔子正东100米处，运动方向始终朝着上一时刻兔子的位置而调整。已知狗的速度是兔子两倍，现需研究兔子能否安全逃回巢穴，并建立如图（1）的平面直角坐标系来描述兔子与狗的运动。

模型假设

1. 假设在运动过程中兔子和狗的速度保持恒定，且不受其他因素的影响。
2. 假设在较短时间内，狗的运动轨迹可以近似看作直线。
3. 假设当狗与兔子之间的距离无限小时，即可认为狗追上了兔子。
4. 假设狗的奔跑方向始终是由D指向R。

符号说明

微分模型建立与求解

由于兔子始终作简单的匀速直线运动，我们主要研究狗的运动情况。
Step1：对狗的运动情况建立微分方程组

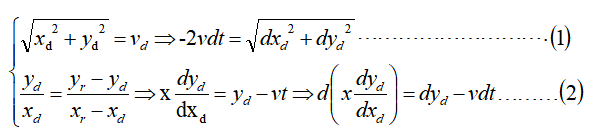
Step2：将(1)中的 dt 代入(2)式，可得

Step3：换元法令z,将初始条件D(100，0)中代入积分，最终解得

Step4：追上兔子时

所以，由理论求解知兔子能成功逃脱，即狗无法追上兔子。

Turtle动画仿真

其中用到的Turtle基本语法可参考这篇文章: 【Python】使用Turtle库画图.

下面通过计算机仿真技术来验证理论求解的结果。使用Python中的Turtle库进行仿真的处理方式与理论求解有一些不同，为了使效果更加显著，需要人为设定一些参数。如下：

1. 设定图例。 图中坐标：真实坐标= 4.8 : 1.
2. 移轴处理。 将原点由兔子的初始坐标移到turtle默认的原点坐标，根据图例重新设定各个标志物的起点坐标，如图（2），巢穴t.goto(-240,-144)，兔子rabbit.goto(-240,144)，狗dog.goto(240,144).
   
3. 规定时间间隔。 计算机无法自动实现趋于无穷小的时间间隔，需要人为设定一个较小的dt（程序中for循环的i即表示该时间间隔），该dt也是程序中更新动画的时间间隔。【其实你可以去尝试一下，dt取值不一样画出来的图真是千差万别~
4. 定义运动函数。
   规定兔子在到达巢穴之前（即i<144），每个单位时间向南移动两个单位长度 rabbit.forward(2)，抵达巢穴后（i>144）不再移动rabbit.forward(0)；
   狗在每个单位时间内移动的距离为四个单位长度dog.forward(4)，其运动方向在每个单位时间内都需根据兔子的方向进行调整，调整角度为：
   
   在兔子到达巢穴前，狗向逆时针方向进行调整dog.left(angle)，当整体调整到90°之后改向顺时针方向dog.right(angle)。如图（3）为定义的完整函数代码。
   
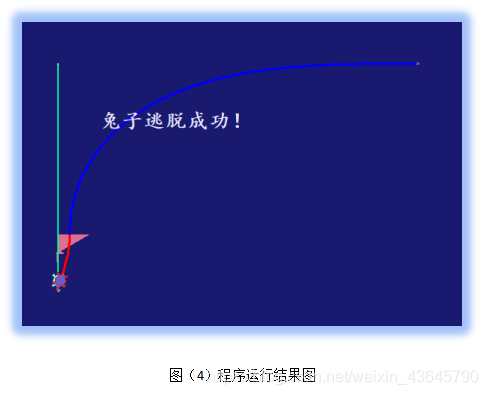
5. 循环处理，得到结果。 如图（4）是动画运行的最后结果，兔子成功逃脱，这也验证了前文的理论计算。
   

模型评价与推广

用简单的微分模型解决了本题后，不禁会思考，如果题目中的初始值没有给定或者给定的是其他更复杂的值，应该如何建模呢？

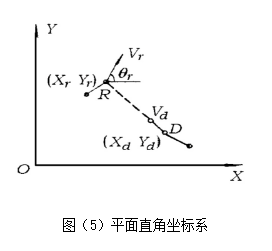
仍然先建立平面直角坐标系来描述运动。如图（5），在任意时刻，兔子的位置R为（xr，yr）,奔跑方向与x轴夹角为，狗的位置D为（xd，yd）,奔跑方向由D指向R。
由运动学公式的微分形式能够计算出t时刻兔子的位置坐标：

狗追兔子过程中仍然满足：

并由（4）可解出狗的运动微分方程：

可由（3）式对（5）式消去时间t，并代入已知的,等初始条件，得到猎狗运动的轨迹方程：

其中a,b是与初始条件有关的参数，将xd0, yd0 代入（6）即可求得一般性的狗的运动轨迹方程 yd，再求该轨迹与兔子轨迹的交点即可知能否追上。

参考文献

[1]强胜,龙汉,申镇,易东云.追踪法推广的数学建模与仿真[J].兵工学报,2009,30(01):56-62.

鸣谢!!!

感谢全宇宙最可爱的秀姐提供的建模思路，最开始考虑的微分模型还是太简单了，就和我的代码一样简单（狗头）。

说实话，接触Python也已经一年了，到现在还是只会基本语法，这次由于疫情困在家中，手中的建模工具好像也只有Python能用，才终于拾了起来。
这个Turtle库真的很好上手，像我这种小白都只用花半天时间，就把狗追兔子的仿真过程水出来了！真！好用！！

附上完整代码

好用！Python

from turtle import * 
import turtle as t 
import numpy as np

t.title("欢迎欣赏这场激烈的狗追兔子比赛")
t.bgcolor("midnightblue")

#兔巢
t.penup()
t.speed(1)
t.goto(-240,-144)
t.pendown()
t.color("palevioletred")
t.begin_fill()
t.left(90)
t.forward(60)
t.right(90)
t.forward(40)
t.right(150)
t.forward(50)
t.end_fill()
t.penup()

#兔子
rabbit=Turtle()
rabbit.hideturtle()
rabbit.shape('turtle')
rabbit.color("paleturquoise")
rabbit.pensize(2)
rabbit.up()
rabbit.goto(-240,144)
rabbit.right(90)
rabbit.showturtle()
rabbit.down()

#定义兔子运动函数
def rabbitmove():
    if i<144:
        rabbit.forward(2)
        rabbit.pencolor("mediumspringgreen")
    else:
        rabbit.forward(0) 

#狗
dog=Turtle()
dog.hideturtle()
dog.shape('turtle')
dog.color("slateblue")
dog.pensize(3)
dog.up()
dog.goto(240,144)
dog.right(180)
dog.showturtle()
dog.down()

#定义狗的运动函数
def dogmove():
    if i<144:
        angle=np.arctan((dog.ycor()-rabbit.ycor())/(dog.xcor()-rabbit.xcor()))
        dog.left(angle)
        dog.forward(4)
        dog.pencolor("blue")
    else:
        angle=np.arctan((dog.ycor()-rabbit.ycor())/(dog.xcor()-rabbit.xcor()))
        dog.right(angle)
        dog.forward(4)
        dog.pencolor("red")
    
for i in range(160):
    rabbitmove()
    dogmove()

printer = t.Turtle()
printer.hideturtle()
printer.penup()
printer.forward(20)
printer.color("lavender")
printer.write("兔子逃脱成功！\n\n", align="right", font=("楷体", 20, "bold"))

好看！MATLAB

a=6;%兔子速度x
b=12;%猎狗速度2x
dt=0.1;%时间的增加
t=0;%初始时间
s=0;%初始路程
d=0.5;%距离小于0.5，代表追上
dog_x=100;dog_y=0;rbt_x=0;rbt_y=0;
hold on
axis([0,150,0,80])
title('狗追兔子问题')
text(0,60,'兔子洞穴A')
text(100,0,'狗初始位置B（100,0）')
text(0,0,'兔子初始位置O（0,0）')
pause(3)
while (sqrt((dog_x-rbt_x)^2+(dog_y-rbt_y)^2)>d) && rbt_y<60 %当兔子和狗距离大于1时，执行以下程序
    t=t+dt;               %计时器加0.1
    dog_x=dog_x-b*dt*dog_x/sqrt(dog_x^2+(a*t-dog_y)^2);   %狗横坐标的实时坐标
    dog_y=dog_y+b*dt*(a*t-dog_y)/sqrt(dog_x^2+(a*t-dog_y)^2);%狗纵坐标的实时坐标
    rbt_y=rbt_y+a*dt;     %兔子纵坐标的实时坐标
    if(rbt_y>=60&&mod(round(rbt_y*15),2)==0) 
        text(10,55,'兔子逃生成功！','Color','red','FontSize',30);
    end
    if(rbt_y>=60&&mod(round(rbt_y*15),2)==1)
        text(10,55,'兔子逃生成功！','Color','green','FontSize',30);
    end
    plot(dog_x,dog_y,'r*',rbt_x,rbt_y,'g*')%绘制曲线
    pause(0.1)%停0.1s
    s=s+b*dt;%狗总路程
end