考研数学考点分析1

小红楼考研Jack老师

已于 2025-03-27 10:37:12 修改

阅读量286

点赞数 4

文章标签：考研数学建模

于 2025-03-05 15:04:47 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_43666218/article/details/146043074

版权

每日定时更新，考研资料免费送，有意者联系下方微信

一函数、极限、连续

1.1函数

1.1.1有界性

有界性定义：

设函数 $f(x)$ 在区间 $I$ 上有定义，如果 $\exists M> 0$ ，使对 $\forall x\in I$ 都有 $\left | f(x) \right |\leq M$ ,则称 $f(x)$ 在区间 $I$ 上有界；若不存在这样的 $M> 0$ ，则称 $f(x)$ 在区间 $I$ 上无界.

考点1 有界性的判定

方法1：函数有界性定义

方法2：函数有界的充要条件是函数既有上界也有下界

方法3：在某点函数极限趋近于无穷大

方法4：常用有界函数

$\left | sinx \right |\leq 1,\left | cosx \right |\leq 1,x\in (-\infty ,+\infty)$

$\left | arcsinx \right |\leq \frac{\pi }{2},x\in \left [ -1,1 \right ] ;0\leq arccosx\leq \pi,x\in \left [ -1,1 \right ]$ $\left | arctanx \right |< \frac{\pi }{2},x\in (-\infty ,+\infty );0< arccotx< \pi ,x\in (-\infty ,+\infty )$

1.1.2单调性

单调性定义：

设函数 $f(x)$ 在区间 $I$ 上有定义，如果对于 $\forall x_{1},x_{2}\in I$ 且 $x_{1}< x_{2}$ 时，恒有 $f(x_{1})< f(x_{2})(orf(x_{1})> f(x_{2}) )$

则称函数 $f(x)$ 在区间 $I$ 上单调增加（减少）的

考点2：函数单调性的判断

方法1：根据单调性定义判断

方法2：图像法

方法3：对于 $\forall x_{1}, x_{1}$ 且 $x_{1}< x_{2}$ ， $f(x_{1})-f(x_{2})< 0(> 0)$ , $f(x)$ 在区间 $I$ 上单调增加（减少）

1.1.3奇偶性

奇偶性的运算性质

（1）奇函数的代数和仍是奇函数；偶函数代数和仍为偶函数。

（2）偶数个奇函数或者偶函数的乘积为偶函数；奇数个奇函数乘积为奇函数。

（3）一奇一偶乘积为奇函数

奇偶性的其他性质

奇函数：

① $f(-x)=-f(x)$ ，奇函数图像和定义域关于原点对称

②奇函数 $f( x)$ 在 $x=0$ 处有意义时（即定义域包含0时），有 $f(0)=0$

③奇函数 $f( x)$ 的最大值与最小值之和为 $0$ 。

④重要结论：已知函数 $g(x)$ 为奇函数， $a$ 为常数， $f(x)=g(x)+a$ ，则有 $M+m=f(x)+f(-x)=f(x_{0})+f(-x_{0})=2a=2f(0)$ 其中 $M$ 表示最大值， $m$ 表示最小值

偶函数：

① $f(-x)=f(x)=f(\left | x \right |)$ 偶函数图像关于 $y$ 轴对称偶函数定义域关于原点对称

②定义域关于原点对称的非零常函数是偶函数。（ $eg:f(x)=1$ ）

③若 $f(x)=a^{2}+bx+c (a\neq 0)$ 为偶函数，则 $b=0$

1.1.4反函数

反函数定义：

反函数求法：

求函数的反函数：

1、判断函数是否是一一对应关系，如果不一一对应则无反函数。

2、将原函数中 $y=f(x)$ ,解出 $x=\varphi (y)$ ,则反函数即为 $y= \varphi (x)$ 。

3、定义域值域互换，图像关于 $y=x$ 对称。

4、牢记初等函数（特别是三角函数、幂指数）的反函数。

1.1.5 初等函数的性质与图像

1.幂函数

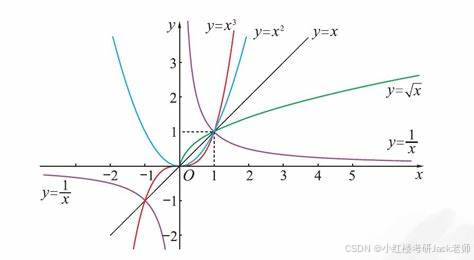
2.指数函数以及对数函数

3.三角函数以及反三角函数

1.2极限

1.2.1极限定义以及左右极限

1.2.2 函数极限的性质

考点：极限局部保号性的应用

保号性首先要求极限存在且极限不等于0，再由极限的正负决定局部范围内f(x)的正负

1.2.3极限的四则运算

1.2.4极限存在准则——夹逼准则

考点：利用夹逼准则求极限

数列极限进行适当的缩放，放大缩小的极限要存在且相等

1.2.5极限存在准则——单调有界准则

1.2.6 两个重要极限

1.2.7无穷小和无穷大及其性质

1.2.8连续性与间断点

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。