Shuffle Differential Privacy(2)

Shuffle Differential Privacy(2)

一、混洗差分隐私的“隐私毯”

The Privacy Blacket of the Shuffle Differential Privacy[1]

关键思想：将LDP报告的分布分解为两个分布，一个依赖于真实值，另一个独立随机。这个独立分布形成了一个“隐私毯”。

毯分解（blanket decomposition）

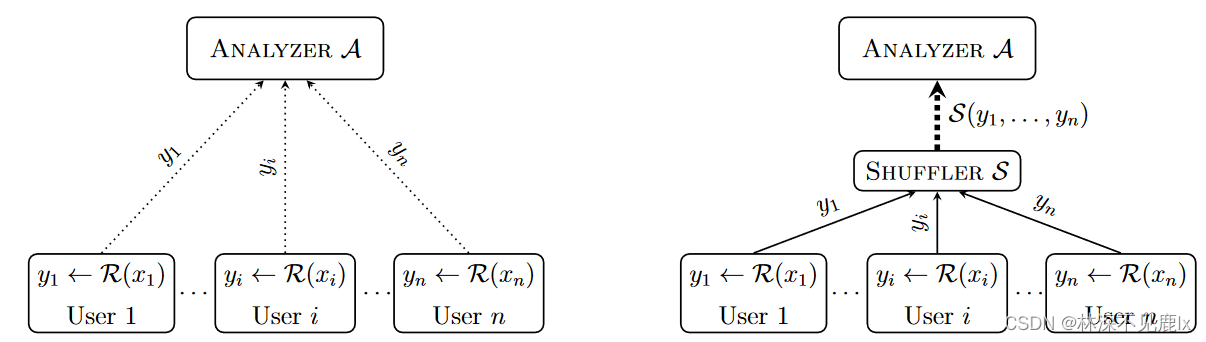
例如，在差分隐私单消息混洗模型 $(R,S,A)$下，有$n$个用户，每个用户$u_i$ 持有一个输入 $x_i$并对其应用本地随机器 $R$获得单个消息 $y_i$，消息 $(y_1,y_2,\dots ,y_n)$被混淆器 $S$打乱以获得 $(y_{\sigma (1)},y_{\sigma (2)},\dots ,y_{\sigma (n)})$，其中 $\sigma$是随机选择的排列，最后由分析器 $R$对 $(y_{\sigma (1)},y_{\sigma (2)},\dots ,y_{\sigma (n)})$进行后处理以得到分析结果。

定义一个概率参数 $\gamma \in [0,1]$，集合 $B$中包含 $\gamma n$个用户，其中的用户将提交随机值，而剩余 $(1-\gamma )n$个用户将提交器其真实值。集合 $B$中的各方发送的值形成均匀随机值的直方图 $Y_1$，而集合 $B$以外的各方发送的值对应于其数据的真实直方图 $Y_2$。因此，在混洗模型中服务器端获得的信息相当于直方图 $Y=Y_1\cup Y_2$。（其中 $Y_1$为本地随机器 $R$的随机毯random blanket）

对于LDP下的GRR扰动协议，其输出分布可以被分解为如下形式：

$$\forall y\in \mathcal{D},Pr[GRR(v)=y]=(1-\gamma )Pr[y|v]+\gamma Pr[Uni(\mathcal{D})=y].$$

上述结论的特例即对二进制数据混洗对应于安全加法（secure addition），当 $k>2$时混洗对应于直方图的安全加法。

那么为了实现差分隐私，需要设置合理的 $\gamma$值使得在相邻数据集上计算时，总分布 $Y$的变化量有使得的限制。（即满足差分隐私的定义）

注意，当发生变化的用户（假设为第n个用户）在集合B中时，其上传的数据是均匀随机选择的，因此可以保证隐私。但若其不在B中，服务器在具有最大背景知识（即知道另外n-1个用户的真实数据）的情况下可以直接推断该用户的真实数据，导致隐私泄露。此时，服务器观察到 Y 1 ∪ { x n } Y_1\cup \{x_n\} Y1​∪{xn​}，即随机直方图与该用户输入的并集。

直观上，协议的隐私性归结为设置 $\gamma$，以便 $Y_1$适当地隐藏 $x_n$

（这里给出了隐私毯privacy blanket的定义，也有文章直接将上述的独立分布叫做隐私毯)

---

二、本地随机发生器 $R$的隐私分析

隐私直方图的本地随机发生器： ${\mathcal{R}}_{\gamma ,k,n}^{PH}$

（该算法简单理解即为上述提到的用户上传随机值或真实值的情况）

下述定理表明了对 $\gamma$适当选择下的协议隐私性：

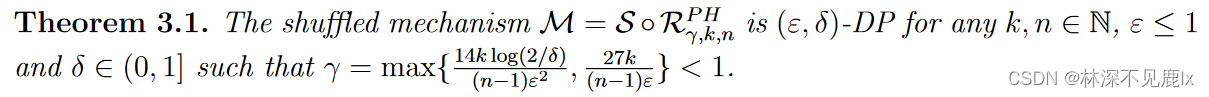
证明主要关注相邻数据集上用户 $u_n$不在集合B中的情况，即该用户上传的是真实值

$n_j=Y_1(j)+\mathbb{I}[x_n=j]$ 即随机分布中值j的数量加上用户n上传的真实数据是否为j（1或0)

所有 $n_j$的和即集合B中的用户总数加上第n个用户： $|B|+1$

假设相邻数据集中 $x_n=1$， $x_n^{\prime }=2$ 则有：


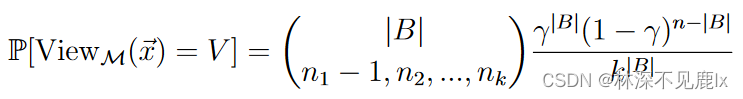
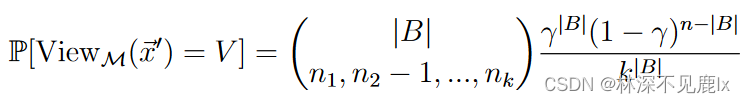
为了保证 $(ϵ,\delta )-DP$，需要证明：

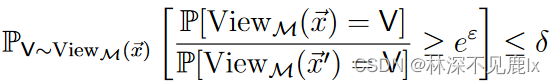
因此代入上述两个概率可以得到：

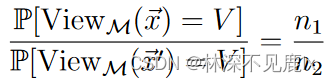
将 $n_1,n_2$表示为表示为二项式分布即可得到：

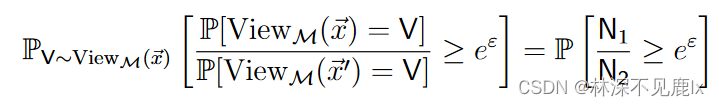
其中 $N_1\sim Bin(n-1,\frac{\gamma }{k})+1,N_2\sim Bin(n-1,\frac{\gamma }{k}).$

接下来使用联合界（Union Bound）和乘法切诺夫界（Multiplicative Chernoff Bound）来限制上述概率：

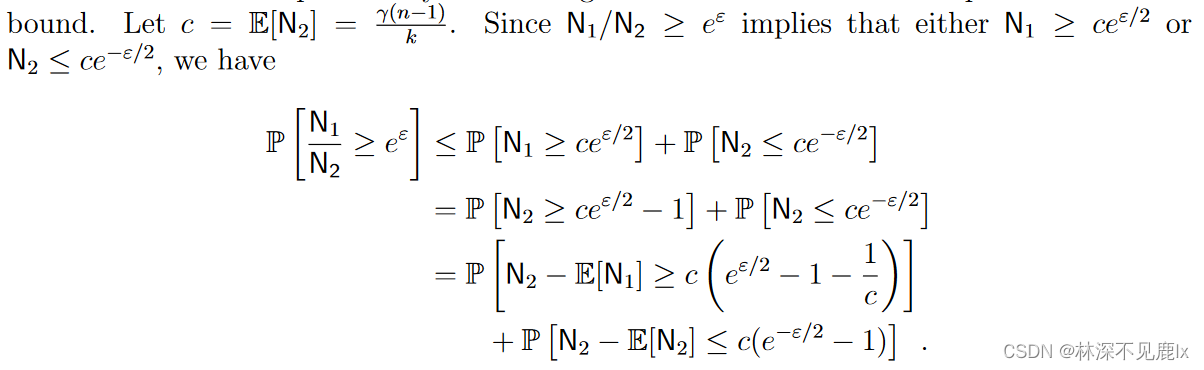
tips:

1. 联合界（Union Bound）是概率论中的一个重要不等式，它用于对多个随机事件的概率上界进行估计。假设有一系列事件 $A_1,A_2,...,A_n$，那么这些事件至少其中之一发生的概率不会超过各事件发生概率之和。数学上可以表示为：

$$[P\left(\bigcup _{i=1}^n{A}_i\right)\le \sum _{i=1}^{n}P(A_i)]$$

1. 乘法切诺夫界（Multiplicative Chernoff Bound）是Chernoff Bounds的一个变种，用于估计独立随机变量之积的概率。假设有一组独立同分布的随机变量 $(X_1,X_2,\dots ,X_n)$，它们的期望值为 $\mu$ 。定义它们的乘积为 $Y=X_1\cdot X_2\cdot \dots \cdot X_n$。其可以表示为：

   $$[P(Y\ge (1+\delta ){\mu }^n)\le e^{-\frac{{\delta }^2\mu }{3}}]$$

将乘法切尔诺夫界限应用于每个概率可以得出:

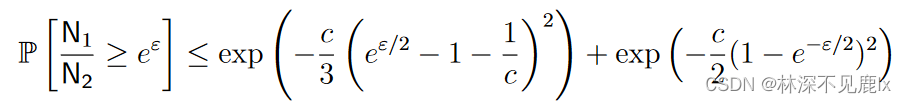
假设 $ϵ\le 1$，则右侧两个被加数都小于或等于 $\frac{\delta }{2}$，如果满足下式：

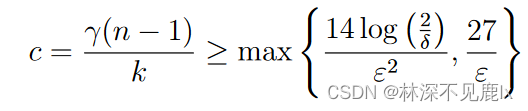
（上述证明在使用切尔诺夫不等式来限制隐私损失随机变量较大的概率时，为了简单起见假设了 $ϵ\le 1$。但在对 $ϵ$没有限制时通过将 Chernoff 不等式替换为 Bennett 不等式来解释尾部边界中隐私丢失随机变量的方差，可以得到类似的结果。）

通过上述对于概率参数 $\gamma$的选择，本地随机发生器R满足 ${ϵ}_0-LDP$，其中:

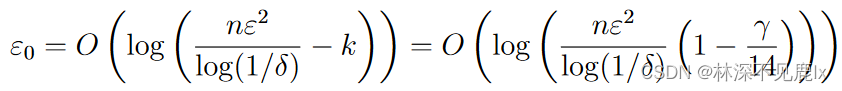
因此上述定理（Theorem3.1）可以被视为隐私放大声明：

注意隐私放大后结果为 $(ϵ,\delta )-DP$而不是 $(ϵ,\delta )-LDP$

---

参考文献：

[1]Balle, B., Bell, J., Gascón, A., Nissim, K. (2019). The Privacy Blanket of the Shuffle Model. In: Boldyreva, A., Micciancio, D. (eds) Advances in Cryptology – CRYPTO 2019. CRYPTO 2019.

[2]Wang, T., Xu, M., Ding, B., Zhou, J., Hong, C., Huang, Z., Li, N., & Jha, S. (2019). Improving utility and security of the shuffler-based differential privacy. Proceedings of the VLDB Endowment, 13, 3545 - 3558.