隐私保护学习笔记（privacy protection reading list）

简介

起因

随着大数据、云计算和移动互联网的快速发展和广泛应用，数据面临严峻的隐私泄露问题，如患者个人信息（身份、家庭、工作等）、采集的病征信息（如脑电、影像等）、以及电子病历信息等。

隐私保护的必要性

最近关于互联网隐私引发大众的关注于讨论，前有Facebook“数据门”，小扎不得不换下常穿的灰色短袖和牛仔装，换上深蓝色西装参加国会听证；后有百度总裁李彦宏称中国用户愿用隐私方便和效率引发网友强烈反感，网友评论说，牺牲隐私不一定换来效率，还可能换来死亡，比如搜索到莆田医院，还可能换来经济损失，比如大数据杀熟等等；近来有知乎强制隐私搜集条款，引发部分用户卸载APP，国内很多APP若不同意给予相关权限，则无法正常使用，这真是陷入两难境地。为什么现在很多应用会收集数据呢，《未来简史》这本书中给了答案——未来的世界数据为王，人类可能只是放大版的蚂蚁，用于产生数据。有了数据后，加上合适的算法可以完成很多事情，这些技术均与机器学习、深度学习以及数据科学相关。人们担心自己的数据被收集后会被泄露或者是被不正当使用，因此，如何将隐私数据很好地保护起来是公司需要考虑的主要问题之一。

隐私保护面临的挑战

1. 传统的被动式隐私保护技术，存储和计算的外包使得数据生成者失去对数据的知情权和控制权。
2. 大数据的多样性带来的多源数据融合，增加隐私泄露的风险。
3. 缺乏大数据隐私泄露后相应的补救措施。
4. 个人隐私和数据的法律法规淡薄。

主要的隐私保护技术

1. 数据扰动
   静态数据发布的匿名模型（如k-匿名）
   动态数据发布的隐私模型（如差分隐私）
2. 基于密码学的隐私保护
   数据加密：同态加密、安全多方计算
3. 数据隐藏
   数字水印
4. 数据使用
   身份认证、访问控制、安全审计等

隐私保护技术介绍

1. 数据匿名化技术

在数据发布时根据某些限制不发布数据的某些域值，方法有泛化、隐匿、交换等，其中，泛化和隐匿最为常用。应用：数据脱敏，数据发布。

泛化：用更一般的值或者模糊的值取代原始属性值，但语义上与原始值保持一致。

隐匿：用最一般化的值取代原始属性值，可视为是最高级别的泛化。

匿名化模型：k-匿名、l-多样性、 t-Closeness、个性化匿名、动态数据匿名化。

GNN重建：利用对抗生成网络进行匿名化。

2. 差分隐私

差分隐私（Differential privacy）是一种被广泛认可的隐私保护模型，它通过对数据添加干扰噪声的方式保护发布数据中潜在用户的隐私信息，从而达到即便攻击者已经掌握了除某一条信息以外的其它信息，仍然无法推测出这条信息。

差分隐私是隐私的严格数学定义。 如果攻击者无法使用辅助信息对敏感数据进行逆向工程，则称该算法具有差分隐私。

差分隐私算法在原始数据中加入随机噪声，使攻击者难以破坏隐私。

隐私损失：通过使用辅助知识重新识别个人，这对个人来说是一个额外的风险。

差分隐私的局限性：可以通过对数据进行重复查询来估计原始数据的详细信息。

差分隐私是保护数据的保证，并解决了在将查询发送到数据集时释放有关特定值的信息的风险。 差分隐私在大数据系统中特别有效，它降低了推理和跟踪攻击的可能性。 考虑一个有兴趣将其用户数据库用于研究目的的组织的场景。 由于数据库包含有关用户的敏感数据，因此组织必须在将其用户数据用于研究之前对其进行匿名化处理。

差分隐私使用合适的算法，向数据集添加足够量的噪声，以确保不会从数据中透露任何关于个人的具体信息。 与添加的噪声相比，添加或删除单个数据点的影响相对较小。 这种机制不会对分析的整体结果造成任何重大变化。

https://www.kaggle.com/code/usharengaraju/differentialprivacy-using-diffprivlib-w-b

3. 同态加密

同态加密，能够在不解密的情况下对密文数据进行计算，使得对该密文的明文执行了相应的计算。解决了密文域的安全计算问题。

根据密文计算能力的不同，可以分类为单同态加密、类同态加密、全同态加密。

4. 安全多方计算

解决一组互不信任的参与方之间保护隐私的协同计算问题，SMC要确保输入的独立性、计算的正确性、去中心化等特征，同时不泄露各输入值给参与计算的其他成员。

主要是针对无可信第三方的情况下，如何安全地计算一个约定函数的问题，同时要求每个参与主体除了计算结果外不能得到其他实体任何的输入信息。

5. 数字水印

将一些标识信息（即数字水印）直接嵌入数字载体（包括多媒体、文档、软件等）当中，但不影响原载体的使用价值，也不容易被人的知觉系统（如视觉或者听觉系统）觉察或注意到。包括图像水印、音频水印、视频水印、文本水印。

应用：版权保护、数字指纹、认证和完整性校验、内容标识和隐藏标识、内容保护、隐蔽通信。

6. 身份认证

分类：

1）根据客观的认证条件，分为双因子与单因子两种不同的认证方式；

2）借助于认证信息的分类，可以分为动态的和静态的认证；

3）从运用硬件还是软件角度，分为软件与硬件两种不同的认证。

身份认证方式：

1）生物特征认证，缺乏准确性和稳定性、成本高；

2）用户名和密码，静态密码、密码容易暴露；

3）USB Key认证，客户端的缺陷、冲击-响应认证不能进行双向认证；

4）动态口令/动态密码，单密钥、成本高。

隐私预算Epsilon (ε)

ε是数据库 (x) 上的查询与数据库 (y) 上的相同查询之间的最大距离。也就是说，它是数据差异变化（即添加或删除 1 个条目）时隐私损失的度量。也称为隐私参数或隐私预算。
隐私预算ε衡量的是隐私保护程度，ε越小，说明对隐私保护程度越高，但同时可能会影响查询结果的准确性。
因此，在实际应用中需要根据具体情况合理设置隐私预算。

https://blog.csdn.net/yunqiinsight/article/details/80177749
https://zhuanlan.zhihu.com/p/478367669
https://blog.openmined.org/privacy-series-basics-definition/

Shuffle DP

所有本地数据经过随机化（LDP）后传入一个洗牌器（可信的洗牌服务器），打乱加噪后数据的分布，获得更高的隐私保护效果（消耗的总$ϵ$变小了）。

隐私放大

利用hockey-stick divergence（曲棍球棒效应）度量本地上传的各方数据间的差异，经过洗牌器打乱后各方数据的hockey-stick divergence下降，根据hockey-stick divergence推测隐私放大。
在这里插入图片描述

The Privacy Blanket of the Shuffle Model

Rényi DP

https://blog.csdn.net/qq_41691212/article/details/122515022

A Course on Differetial Privacy taught by Gautam-Kamath

长江学者推荐

Lecture 1. Some attempts at data privacy

Example 1: New York city Taxi and Limo Commission

两个数据集：fares + trips 共19GB 包含2013年纽约所用出租车的fares 和trips
其中包含很多属性，例如用户taxi ID、终点、起点时间等等，可推测sensitive information 例如 home locations 、user wealth

上图对medallion，hack_license等敏感数据进行了加密，看上去好像很难获得有效的信息。

但因为主键具有唯一标识性，或加密方法暴露，攻击者可以通过medallion，hack_license获得一些信息，例如：

这样的攻击叫做Data linkage attack，虽然不可以认证唯一的用户，但很重要，因为它们很常见。它可以通过这个数据集链接到其他数据库，一定程度上可以暴露一些重要数据。
例如：如果我们知道hack_license的一个真实数据123456，但我们不知道是其中哪个。在Data linkage attack中，将这个数据映射到其他带有真实用户名的数据集时，这就是一次真实的隐私侵害。此外，根据原数据集也能推测出该用户的收入，位置。

Example 2: Netflix Prize

Recommendat engine 2006-2009
利用奖励收集观影者Netflix数据集，与公开数据集匹配，识别用户。

Example 3: Memorization in Neural Networks

这是一个生成语言的案例，叙述的是一个基于曝光的测试方法，旨在探究神经网络的记忆性。

作者往语料库中加入canary（噪声），在生成的数据里测试出现相同canary的概率。结果证明，语料库越大，canary出现的概率越小。

作者提到的保护方法：可以对唯一序列的发生率和采样率进行限制，并且可以在训练过程中添加裁剪和差分隐私噪声。

Example 4: Genomic Studies

这是一个关于医学或基因数据的案例，叙述了基因组数据有识别个人的风险，同时也是开放科学的障碍。

Example 5: Massachusetts Group Insurance Commission

讲述的案例是来自一个州的雇员的医院就诊记录信息是高敏感的，原始数据集包括了个人姓名、SSN、邮政编码、出生日期、性别和身体状况等信息，但通过删除个人姓名和SSN等识别特征实现匿名。

但有研究人员使用选民名册的信息与”匿名“后的就诊记录匹配，可以很容易对个体进行再识别。

该例子的保护方法是使用k-匿名的方法，泛化某些数据的精度，例如年龄：将具体的32岁，改为<=35岁,是攻击者只能知道目标范围而不能唯一标识个人。

Lecture2: Reconstruction and a Census

Cracking Aggregation

人口普查从一个人口中收集数据，包括每个人的年龄、性别、种族等领域。这种原始数据的集合被称为微数据（microdata）。然而，这些数据通常被认为是个人身份（由法律法规执行），因此，通常只发布聚合统计数据。

例如，通过注意到有4个黑人和3个黑人女性，我们可以推断只有1个黑人男性——在这里释放中位数或平均值就等于释放他的确切年龄，我们认为这侵犯了隐私。

但我们注意到这组集合统计数据为我们提供了关于同一个人的冗余信息。这些冗余将使我们能够对可能产生给定的聚合物的微数据形成约束。如果有足够多的约束条件，唯一可行的微数据将是真实的攻击这就是重构攻击。

Reconstruction Attack(重构攻击):

1. Generate constraints
2. Find a feaseasible point

Abowd写了一篇推特，描述了内部执行的攻击，其中，根据汇总的统计数据，他们能够准确地重建46%的人口的微数据，并允许71%的人口的±1岁的年龄错误。将其与商业数据库联系起来，使他们能够正确地重新识别超过5000万人的名字。

Queries, Blatant Non-Privacy, and the Dinur-Nissim Attack

数据分析人员需要访问某些类型的查询，而管理员必须“保护数据集中个人的隐私”。
数据分析人员将能够询问“有多少行满足（标识符上的条件）有‘患了疾病？= 1’?"，例如（标识符上的条件）可以是“Name=Alice或Charlie或David”——这个查询的真正答案是2。更抽象地说，我们将假设分析人员可以指定作为[n]的一个子集的查询。设S∈{0,1}的n次方是一个查询向量，对于包含在子集中的索引为1，对于不包含在子集中的索引为0。我们调用这些子集查询（subset queries），注意到，要指定这些查询可能相当复杂——我们暂时回避这个问题，但将在讨论the Cohen-Nissim attack时重新讨论它。查询S的真正答案是A (S) = d·S，即d和S的点积。

管理员将接收一个查询集S，并输出一个响应r (S)。请注意，如果他们简单地输出r (S) = A (S)，这将很容易受到隐私侵犯：分析师可以问一个查询S = {i}，这将揭示个体i的秘密位。结果是管理员将输出一个“噪声”版本的r(S)：将输出一个r(S)，这样|r (S)−A(S)|≤E一些绑定E。注意，我们不要求这种差异r (S)−A(S)是随机分布的——管理员可能输出任何r (S)距离内的E(S)。

保护者提供统计数据，仍然会暴露用户的个人信息。即使保护者提供有噪声的统计数据，仍然可以恢复大部分人的个人信息。
给了一组数据，标明每个人有无疾病。如果问A,B,C,D,E 里有几个有疾病，可以通过内积的方式获得真实值，即S*d, S表示[A,B,C,D,E]是否被询问，如问A,B,E，则d为[1,1,0,0,1], d表示[A,B,C,D,E]是否有疾病，恒等于已知数据[1,0,1,0,1]。

无保护情况：
保护者接受S询问，返回R(S)，即true answer。但由于询问者可以只问一个人的疾病情况，则会暴露隐私。

保护情况：
保护者提供有噪声的统计数据。馆长会提供一个非0的噪声，并且加噪后的数据很接近于真实数据，差值小于E。

我们注意到，一个公然非私有的算法确实是对隐私的公然侵犯。这意味着对手可以在99%的条目上构建一个与真实数据库一致的数据库！因此，我们称之为重建攻击（reconstruction attacks）。我们将证明，相当一般的计划是公然的非私有的。

特别是，如果E = n/401，那么对手可以在99%的条目上匹配真正的数据库。此外，如果E = o (n)，则该算法是明显非私有的。

Proof.！！！

• 攻击：如果允许攻击者提出$2^n$个子集查询（相当于遍历每个可能性），并且保护者被要求以一定的限制E添加噪声，那么攻击者可以根据结果在4E个位置之外的所有位置重建数据库。

• 分析：对于所有dataset的候选组C，如果同时满足
  a.没有疾病的情况下，无疾病的C中的项的总和，与加噪后的所有项的总和，差值小于等于E；
  b.没有疾病的情况下，无病的真实项的总和，与加噪后的所有项的总和，差值小于等于E；
  则暂时保留这个C，无疾病的C和D项之间的差值小于等于2E。
  此外， 针对保留的C，有疾病的项也满足上述条件，则最终留下的候选组C。
  有疾病和无疾病两种情况合并，则C和D之间的差值小于等于4E，最终能够保证在4E个位置之外的所有位置重建数据库。

简单的说，如果分析人员能够用以O (n)为界的噪声询问2的n次方个查询，那么对手就可以（本质上）重建整个数据库。虽然我们得出了一个明显的无隐私行为的有力结论，但它要求分析师以指数级的方式询问许多问题（局限性）。因此，这种攻击在实践中不太可能有效。

（事实上，这种攻击可以得到加强——正如Dwork、麦克雪利和Talwar所显示的那样，即使管理者以任意的噪音大小做出一定比例的反应，对手也有可能成功。

难点

anti-concentration：

事实上，这个隐私上限也会“缩小”，因为我们要求的查询远少于n个(在某些“大数据”规模的应用程序中可能很大）。如果分析人员只询问m<<n个查询，那么管理员只需要添加O（根号m）的噪声。

Linear Reconstruction in Practice

以航空斗篷公司提供了“用于匿名数据重新识别的赏金计划”案例。
数据集中的每个用户都有一个唯一的客户机ID，我们称之为客户机ID。问题是是否有一个函数接收客户端id并将它“足够随机地”地包含在查询集中？它们使用由四个变量指定的函数： mult、exp、d、pred。前三个变量是数字，第四个变量是一个谓词，它接受一个数字，输出真或假。如果一行满足以下条件，则查询将包含在它中：（多*客户端id）^exp的第d位是否满足pred？举个例子，假设mult是17，客户端id是1，exp 0.5，d是3，pred是“数字是偶数吗？”

他们只有一个条件作为开销，只向每个查询添加恒定的多余噪声——远低于Dinur-Nissim攻击可以处理的O(根号n)！所以说，定理3可以轻松实现真实的重构攻击。

Lecture 3 Intro to Differential Privacy

Randomized Response

$\gamma$ = 1/2时对应于第一个真实的答案，$\gamma$ = 0时是第二个均匀随机答案。$\gamma$在0到1/2之间时，答案的正确率随着$\gamma$接近0（对应于更强的隐私），错误就会增加（或者，使用第二个措辞，样本复杂性）。

所以，如果需要在隐私保证的情况下，我们的分析数据达到一定的准确性，需要更多的数据。

问题：随机响应的隐私保护性能分析：

注意，随着γ接近0（对应于更强的隐私），错误就会增加（或者，使用第二个措辞，样本复杂性）。这是很显然的：如果我们想要的隐私保证越强，我们就需要更多的数据才能达到同样的准确性。

Differential Privacy

使用差分隐私算法M后，任意两个数据集的差异都满足上式。个人理解是所有数据集经过差分隐私算法加噪后，就很难区分任意一个数据集与其他数据集，有点匿名化的意思。

差分隐私用法的讨论

• 小的ε对应于强大的隐私，随着ε的增加而退化。
• ε被认为是一个较小的常数，这更可能是合理的隐私保证（更小对应更强的隐私）
• 最坏情况下的保证，对所有邻近的数据集X和X’，都进行随机生成（ε=0），但这是不可能的。
• 换句话说，该定义限制了M的输出满足任何事件的概率的乘法增加（通过改变数据集中的单个点而引起的）。
• 上式的定义是对称的，X和X’是可交换的
• 可以考虑M (X)和M（X’）分布的“接近性”的其他概念。TVD就是如此。
  
• 我们通常会使用“相邻数据集”的概念，其中X中的一个点被任意地改变后得到X’，有时被称为“有界”差异隐私；而在“无界”差异隐私中，一个点要么被添加或删除。

差分隐私的优点

1. 可以防御之前提到的数据链接攻击和重建攻击；
2. 不妨碍统计数据和机器学习；
3. 不适用于目标是识别特定个人的情况，这与该定义相反；
4. 差异隐私的定义在本质上是信息理论的。这与密码学相反，密码学通常侧重于有计算限制的对手。

Randomized Response, Revisited

基于随机响应的差分隐私提供了比中心化差异隐私更强的隐私保证，它提供了局部差异隐私。

Lecture 4 — Intro to Differential Privacy, Part 2

Laplace Mechanism

提到随机响应的不足：应用在非0/1的场景的信息损耗较大。
拉普拉斯机制的优点：可以直接处理任何类型的数字查询。

l1-敏感度：敏感度是一个自然的量。其直观动机是通过修改一个基准点来确定函数的 "变化程度 "的上限。
拉普拉斯分布：可以被看作是对称的指数分布。指数分布只支持在x∈[0，∞)和密度∝exp（−cx），而拉普拉斯分布支持在x∈R上，有密度∝exp（−c|x|）。
拉普拉斯机制：

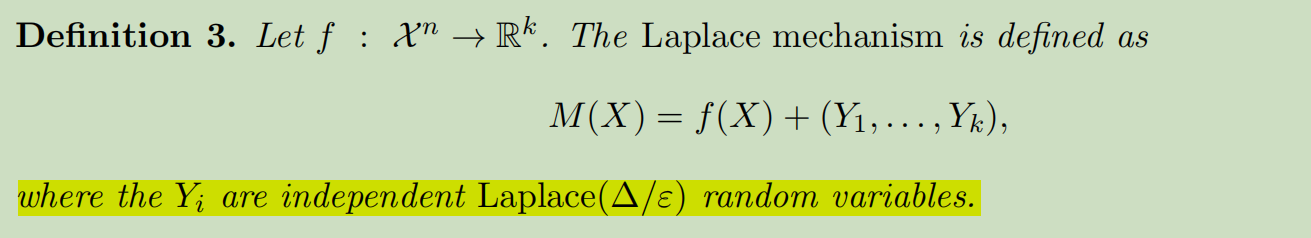
拉普拉斯机制加噪前后的偏差量级为O(1/εn)，而随机响应机制加噪前后的偏差量级为O(1/ε根号(n))。同等量级加噪情况下，随机效应机制会比拉普拉斯机制的隐私界限更高，但数据精度也更低了。

拉普拉斯机制符合ε-差分隐私
任意两个相邻集合加噪后最多相差exp(ε)个量级

Counting Queries

简单的说：做加法，得到单个值。例如：数据集中有多少人拥有属性P？
1 query：sensitivity Δ = 1 , noise = Lap(1/ε), 预算 = ε, error = O(1/ε)
k queries：sensitivity Δ = k , noise = Lap(k/ε), 预算 = ε, error = O(k/ε)

Dinur-Nissim attacks

• 分析者询问Ω(n)计数查询，由管理员使用O（根号n）量级的噪声进行防御，分析师依然可以重建数据库，并导致明显的无隐私。
• 如果分析者询问O (n)计数查询，并且管理员添加了O（n/ε）量级的噪声，那么隐私就得到了保护。

讨论：是否有更强大的攻击，让对手在更多的噪音下成功？或者我们可以减少噪音同时保持隐私？
结论：后者是正确的，并且可以通过更好的分析（以及对差异隐私的定义的轻微放松），使用所谓的高级组合来添加更少的噪声。

Histograms

简单的说：得到多个值，做统计。例如：数据集中有多少人X岁了？

这个函数的$l_1$-敏感性为2：改变任何一个人的年龄都会导致一个计数减少，另一个计数将会增加。

• 统计直方图中，误差的大小只与数据集的数量成对数关系，而不是以计数查询次数的线性有关。

Properties of Differential Privacy

差分隐私获得成功的原因之一是“用户友好”。

Post-Processing
一旦一个数据被私有化，如果数据不再被再次使用，它就不能被“非私有化”。换句话说，只有被“非私有化”的数据才可以被使用。

Group Privacy
两个隐私数据集随着相邻距离的增加，隐私界限呈现指数级增大。

(Basic) Composition
假设在同一数据集上运行了k个不同的ε-差分隐私算法，并发布了它们的所有结果，将获得kε-差分隐私算法的效果。（差分隐私算法性能可以叠加）

Lecture 5 — Approximate Differential Privacy

本课时学习由Dwork、肯塔帕迪、麦克雪利、米罗诺夫和Naor首次提出ε-差异隐私的放松机制。这种放松将具有略微较弱的隐私保护，但允许我们添加显著更少的噪音来实现近似的隐私保护。

Approximate Differential Privacy(($\epsilon ,\delta$)-DP)

新出现的隐私参数 𝛿 表示不满足此近似差分隐私定义的”失败概率”。有 1 − 𝛿 的概率获得等价于纯粹差分隐私的隐私保护程度。同时，有 𝛿 的概率不满足隐私参数为 𝜖 的纯粹差分隐私。

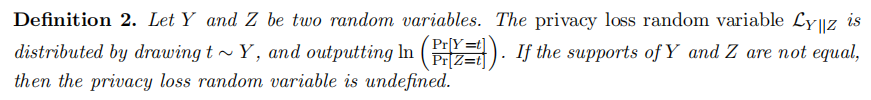
我们有 𝛿 的概率无法保证差分隐私，这意味着我们甚至可能有 𝛿 的概率泄露整个敏感数据集！因此，我们通常要求 𝛿 很小。一般来说，我们要求 𝛿 的取值小于等于 1/n，其中 𝑛 表示数据集的总大小。

Example1：有 1 − 𝛿 的概率满足 𝜖-差分隐私。然而，灾难机制同时有 𝛿 的概率泄露无噪声的整个数据集。
Example2：除非是𝛿极小于1/n，否则至少有一个人的数据是会被明确输出。

proof

catastrophic failure
灾难机制（可能是拉普拉斯机制的情况）有 1 − 𝛿 的概率满足 𝜖-差分隐私。然而，灾难机制同时有 𝛿 的概率泄露无噪声的整个数据集。尽管该机制满足近似差分隐私定义，但我们在实际中不太可能会应用此机制。大多数 (𝜖, 𝛿)-差分隐私机制不会出现类似的灾难性失效情况（如下），比如R´enyi DP， concentrated DP，高斯DP。

detail:

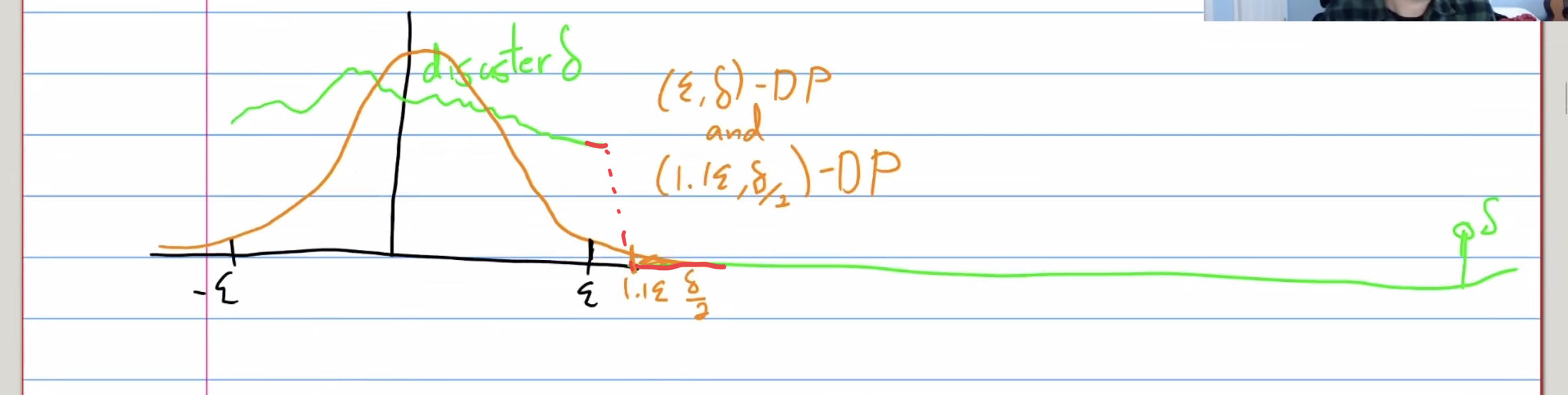
问题
{1, . . . , 1/𝛿}怎么理解？

答：如果一个数据集直接加上一个在{1, . . . , 1/𝛿}内随机数进行简单的输出的算法（下式），这将不满足差分隐私以及任何形式的意思保障。以及如果类似的隐私损失随机变量，可能导致输出真实的结果。

Gaussian Mechanism

L1 and L2 sensitivity
L1：给定长度为 k的向量 V ，其 L1范数定义为$||V|{|}_1={\sum }_{i=1}^k|V_i|$。（即向量各个元素的和）。在二维空间中，两个向量之差的 L1 范数就是它们的”曼哈顿距离”。
L2：给定长度为 k的向量 V ，其 L2范数定义为$||V|{|}_2=\sqrt{{\sum }_{i=1}^k{V}_i^2}$。（即向量各个元素平方和再求平方根）。在二维空间中，两个向量之差的 L2 范数就是它们的”欧氏距离”。L2 范数总是小于或等于 L1 范数。
L1和L2具有以下关系：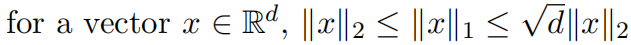
因此，L2的敏感性可能比L1的敏感性低$\sqrt{d}$倍。

Gaussian distribution
单变量的高斯分布$N(\mu ,{\sigma }^2)$，均值为$\mu$，方差为${\sigma }^2$。

Gaussian mechanism

也可以用多元高斯分布将其写成$f(X)+Y$，其中$Y\sim N（0,2ln(1.25/\delta ){∆}_2^2/{\epsilon }^2\cdot I）$，$I$代表一些其他操作。

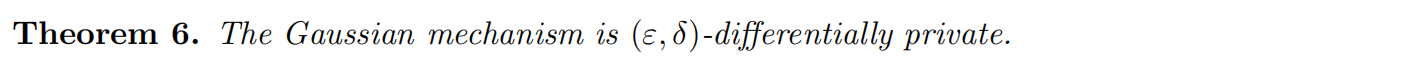
相比拉普拉斯机制，高斯机制可以增加一个更少的$O（\sqrt{d}）$噪声（尽管隐私保护稍弱），从而表明在某些情况下它可能更适合于多元问题。

Properties of Gaussian mechanism

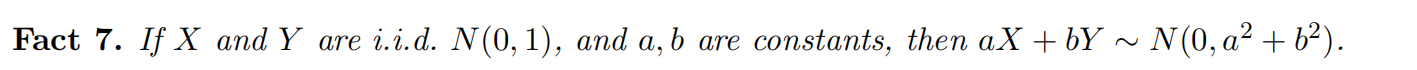
### Properties of ($\epsilon ,\delta$) - Differential Privacy（Catastrophe Mechanism）

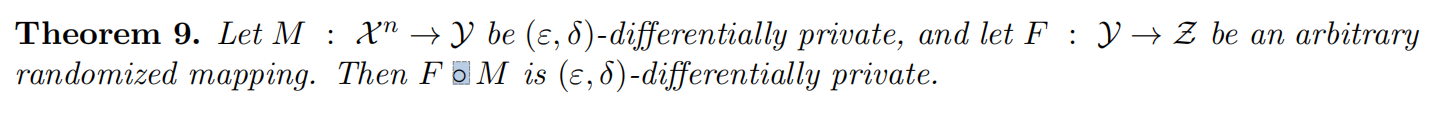
Post-Processing
如果使用了近似差分隐私机制对数据进行保护依然满足差分隐私的后处理特性，那么在得到加噪后的结果之后，可以再次应用相同的机制并使用不同的噪音来提高隐私保护级别。
Group Privacy
考虑k个项不同而不是1个项不同的数据集时，群隐私在近似DP下不如纯DP清晰。需要有一个额外的因子$e^{(k-1)\delta }$。

(Basic) Composition

在同一敏感数据集上运行k个私有分析，可以方便地将ε和δ相加以作为最终的隐私保证。

Lecture 6 — Advanced Composition

当使用高级组合性时，前述要求各个机制均需满足纯粹 𝜖-差分隐私。然而，如果各个机制满足 (𝜖, 𝛿)-差分隐
私，高级组合定理同样适用。

回顾一下上一节课中的多元均值估计的例子。结果表明，使用拉普拉斯机制和高斯机制得到的$l2$误差分别为$d^{3/2}/\epsilon n$和$d/\epsilon n$。可以让高级组合与拉普拉斯机制结合，使拉普拉斯机制也能实现大约$d/\epsilon n$的误差，尽管代价是放松到近似微分隐私。

理解：DP高级组合与串行组合的区别
串行组合：每次加的噪声$\epsilon$是一样的。
高级组合：每次加的噪声$\epsilon$随着查询次数的增加而改变。开始加大噪声比原$\epsilon$更大，但随着查询次数k增加，加的噪声会逐步减少，一般k大于70后加的噪比原$\epsilon$少。

Reduction to Binary-ish Mechanisms

教授希望讨论满足$(\epsilon ,\delta )-DP$隐私保证的最简单的随机变量是什么。
以下是最简单的随机变量表示：

其中一对候选随机变量如下，它具有结果类型的“类型”：一个用于捕获概率为$\delta$的“灾难性失败”，另一个作为“状态 quo”的$e^{\epsilon }$的乘法保证。对于前者，有“I am U”和“I am V”的结果，对于后者，简单地使用0和1。随机变量的描述如下表所示：

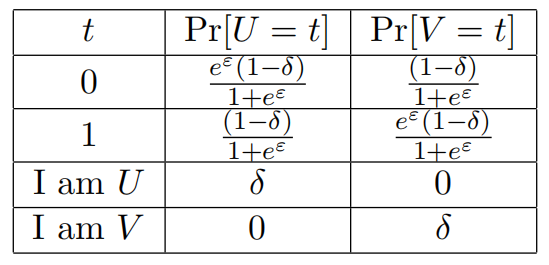
这里声称这对“简单”的随机变量足以表示任何一对具有有界隐私损失的随机变量。

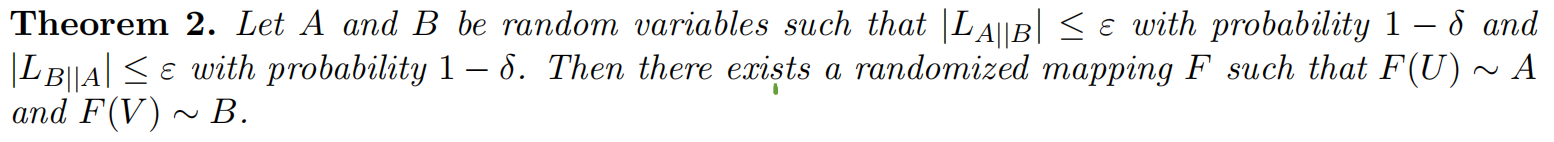
这个定理本质上说我们可以首先从一个简单的分布（U或V）中采样，然后将其映射到一个更复杂的分布中的样本中。
四个结果可以适当地映射到域的相应子集（以某种依赖于A和B的非均匀方式）：

输出结果"I am U"、“I am V”、0、1被映射到点x，被表示为：$L(x)>e^{\epsilon },L(x)<e^{-\epsilon },0\le L(x)\le e^{\epsilon },-e^{\epsilon }\le L(x)\le 0$。
这样做的好处是：只要检查U和V之间的隐私损失行为就足够了，因为通过后处理，A和B也会有隐私损失情况。

进一步，我们可以研究如何从一组不同的私有算法序列简化为一组简单的随机变量序列：
M代表一个$(\epsilon ,\delta )-DP$

只要我们可以证明（U1，…，Uk）和（V1，…，Vk）之间的隐私损失随机变量是适当的有限的限制，那么差异隐私的后处理性质（即，当我们应用F∗）将意味着对M (X)和M（X’）的也具有相同的隐私保证。

Composition of Binary-ish Mechanisms

本例在二进制机制下证明两个随机序列$(U_1,...,U_k)$和$(V_1,...,V_k)$的在以$\tilde{\epsilon }$为边界,$1-\tilde{\delta }$概率下的隐私损失随机变量的绝对价值。

设$z_j$是一个序列中的第$j$个随机变量，且序列内的每个变量都是独立的。且当$z_j$为"I am U"时我们认为隐私收到了侵犯。有：

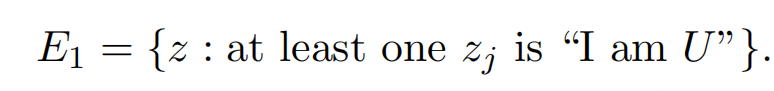
可得到序列中出现$E_1$的概率为：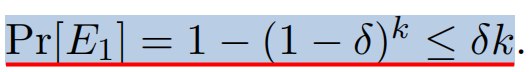
$E_2$表示隐私损失随机变量差距较大的事件。

可以对独立的变量Z使用 Chernoff bound公式：

将下值代入可得到
对在$\overline{E_1},\overline{E_2}$边界的输出（大部分的事件会在这里发生）

将所有可能的发生事件结合可以得到（前面有下划线的式子）：

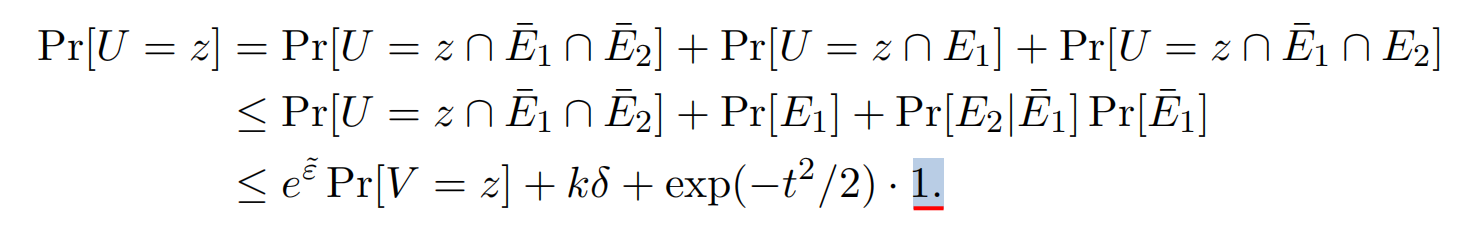
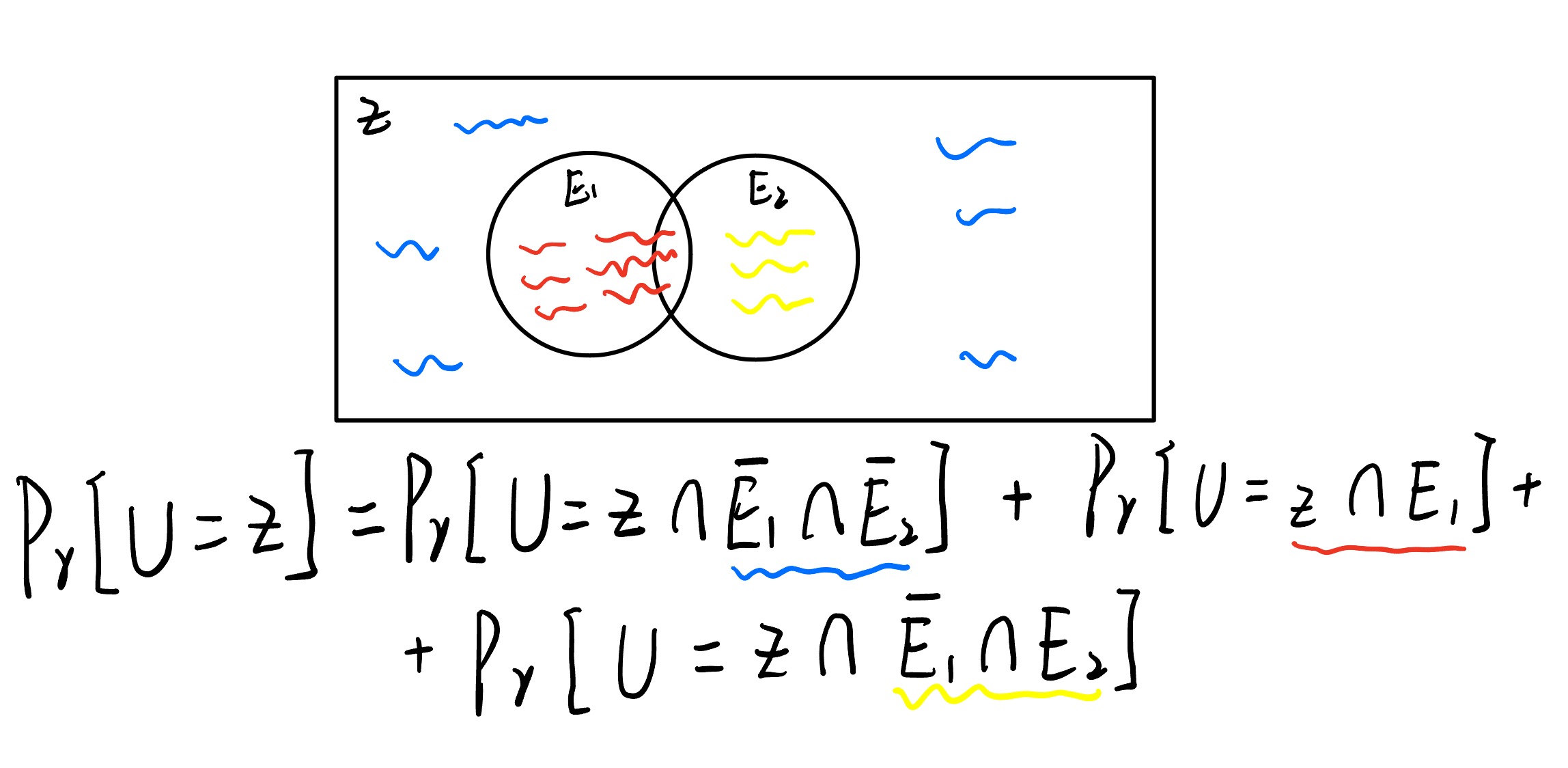
即：后面的$k\delta +exp(-t^2/2)\ast 1$可以当作$\tilde{\delta }$
理解：大部分差分隐私后的变量都出现在$\overline{E_1},\overline{E_2}$边界内，只有小部分（小概率）情况出现在$E_1,E_2$内可能发生灾难性失效。

Lecture 7 — Exponential Mechanism

我们已学习的基本机制（拉普拉斯机制和高斯机制）针对的都是数值型回复，只需直接在回复的数值结果上增加噪声即可。**但如果我们想返回一个准确结果（即不能直接在结果上增加噪声），同时还要保证回复过程满足差分隐私，拉普拉斯机制和高斯机制无法做到这点。**一种解决方法是使用指数机制（Exponential Mechanism）。此机制可以从备选回复集合中选出”最佳”回复的同时，保证回复过程满足差分隐私。分析者需要定义一个备选回复集合。同时，分析者需要指定一个评分函数（Scoring Function），此评分函数输出备选回复集合中每个回复的分数。分数最高的回复就是最佳回复。指数机制通过返回分数近似最大的回复来实现差分隐私保护。

和我们之前学习过的机制（如拉普拉斯机制）相比，指数机制最大的不同点在于其总会输出集合R中的一个元素。

指数机制的输入

只有数据集 $X$是隐私信息，$H$ 是公开的目标信息。以下为问题定义的敏感度：

其中$X^{\prime }andX$是相邻数据集。

Exponential Mechanism 指数机制定义

证明：

理解：

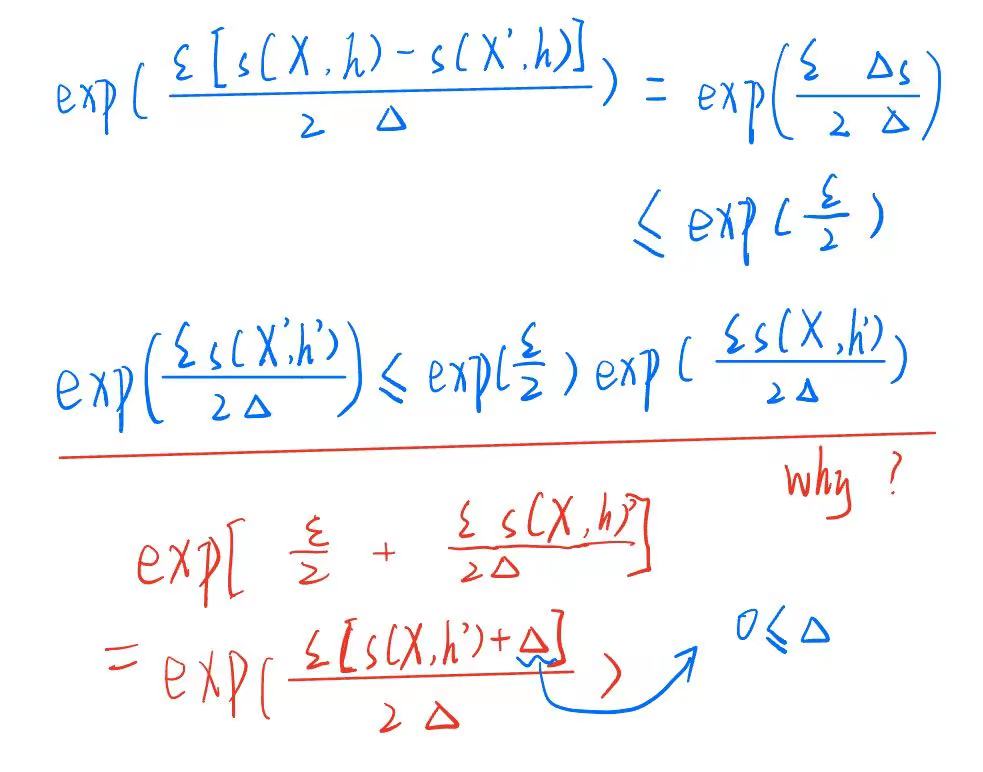
Utility

指数机制允许我们私下选择一个得分与最佳值相当的对象——特别是，我们将损失一个小的加量，这取决于灵敏度、ε和候选对象的数量。它的效用由以下定理来描述。

指数机制的有趣之处在于：

• 无论 ℛ 中包含多少个备选输出，指数机制的隐私消耗量仍然为 𝜖。
• 无论 ℛ 是有限集合还是无限集合，均可应用指数机制。但如果 ℛ 是无限集合，则我们会面临一个非常有挑战的问题：如何构造一个实际可用的实现方法，其可以遵循适当的概率分布从无限集合中采样得到输出结果。
• 指数机制代表了 𝜖-差分隐私的”基本机制”：通过选择适当的评分函数 𝑢，所有其他的 𝜖-差分隐私机制都可以用指数机制定义。

Application

Laplace Mechanism

Selling One Digital Good
场景：卖家有无限的物品供应。有$n$个买家个体，每个个体的值$v_i\in [0,1]$。卖家需要选择一个价格$p\in [0,1]$：如果$p\le v_i$，买家将购买一个项目的副本，卖家从他们那里收到收入$p$，否则卖家不购买该项目，卖家收到收入0。因此，总体收入是$p|i:p\le v_i|$。卖方被迫以一种差分隐私的方式来选择价格。
做法：

1. discretize the domain：由于$p\in [0,1]$，我们让回复目标集合为$H=\alpha ，2\alpha ，\dots \dots ，1$，可观察到$|H|=1/\alpha$。
2. 这种离散化使我们损失了多少？有$\gamma =max{p}_p|i:p\le vi|$，可以得到$OPT(v)\ge \gamma -\alpha n$($\alpha$是得分最小的情况，所以必然满足)。
3. instantiation实例化：卖家的收入可以表示为$p|i:p\le vi|$，当一个买家的购买意向发生变化时，卖家收入的变化为p，且$p\le 1$，所以敏感度$∆\le 1$。
4. 根据Corollary 4 可以得到总收入至少为$\gamma -\alpha n-log(1/\alpha )/ϵ$
   
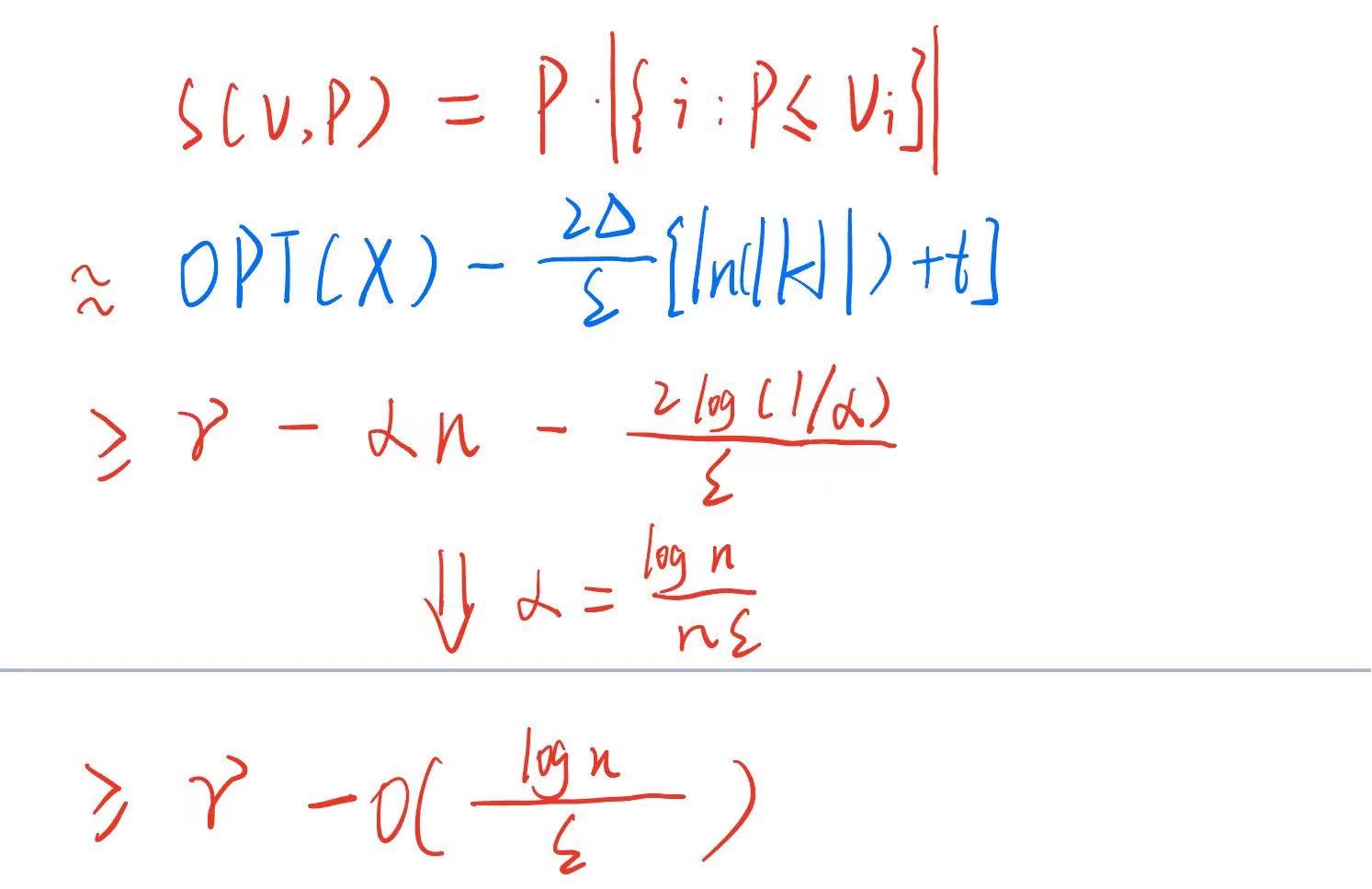
   Private PAC Learning
   算法给出一个数据格式$C:c:{0,1}^d\to 0,1$：该数据集由数据集点和标签组成。数据集中有n个相同数据格式的元素，有一个判别函数$c^{\ast }$可以区分出两个类别（机器学习学习的目标函数），而我们的目标是是差分隐私输出后数据集可以得到判别函数$\hat{x}$尽可能接近$c^{\ast }$。
   
   
   
   定理5、6没有证明

理解

Exponential Mechanism是针对的场景是必需要输出原集合出现的数的情况，通过对原集合中各个相同元素占总数的比例作为概率，然后对概率做差分隐私，再按加噪后的概率输出值。我们课题中对马尔可夫概率矩阵加噪其实就是用的Exponential Mechanism。

https://www.bilibili.com/video/BV1k54y1x7Ua/?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click&vd_source=6f4d58f2911ca74aae4c08e71feb11f0
http://www.gautamkamath.com/CS860-fa2020.html
https://www.youtube.com/watch?v=FJMjNOcIqkc&list=PLmd_zeMNzSvRRNpoEWkVo6QY_6rR3SHjp
《手动学差分隐私》