贪心算法学习

贪心算法

1.算法定义

在对问题求解时，总是做出在当前看来是最好的选择，不从整体最优上加以考虑，只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

2.算法步骤

1.建立数学模型来描述问题；
2.把求解的问题分成若干个子问题；
3.对每一子问题求解，得到子问题的局部最优解；
4.把子问题的局部最优解合成原来问题的一个解。

3.算法应用

各种调度问题，找零问题，区间问题，分配问题等可以分解为子问题并需要求最优解的问题上
贪心算法的基本要素
1.所求问题的整体最优解可以通过一系列局部最优的选择得到
2.题具有最优子结构性质，当一个问题的最优解包含其子问题的最优解时称此问题具有最优子结构性质
最优子结构：
问题能够分解成子问题来解决
子问题的最优解能递推到最终问题的最优解

示例

题目1.分配问题
多指有资源需要分配给不同的需求，要求如何分配才能满足更多的需求
有一批集装箱要装船，集装箱 i 的重量为wi ，轮船最大载重量为c
要求：在不受体积限制的情况下，将尽可能多的集装箱装船

给定：c>0, wi>0, 1≤i≤n
要求：找出一个n元0/1向量x=(x1,x2,…,xn) 其中 xi∈{0,1}
使得：$\sum _{i=1}^n{w}_i{x}_i\le c$
，而且 $\sum _{i=1}^n{x}_i$达到最大

设：集装箱已按重量从小到大排序
设：X=(x1, x2,…, xn)是最优装载问题的一个最优解
设：k = min{ i | xi=1, 1 ≤ i ≤ n }（第一个非零元素的下标）
易知，如果给定的最优装载问题有解，则1 ≤ k ≤ n
当k=1时， X 是一个满足贪心选择性质的最优解
当k>1时，取y1=1; yk=0; yi=xi, 1 < i ≤ n , i ≠k, 则：
$\sum _{i=1}^n{w}_i{y}_i$=($w_1-w_k$)+$\sum _{i=1}^n{w}_i{x}_i\le \sum _{i=1}^n{w}_i{x}_i\le c$
因此： Y=(y1, y2,…,yn)是所给最优装载问题的可行解
由于： $\sum _{i=1}^n{y}_i$=$\sum _{i=1}^n{x}_i$
故：Y也是满足贪心选择性质的最优解
因此：最优装载问题满足贪心选择性质！

最优装载问题具有最优子结构性质
设X=(x1,x2,…,xn)是载重量为c，集装箱为{1,2,…,n}的最优装载问题满足贪心选择性质的的一个最优解
由该问题的贪心选择性质易知：x1=1
且X’=(x2,x3,…,xn) 是如下子问题的最优解
载重量为c-w1，集装箱为{2,3,…,n}的最优装载问题
因此：最优装载问题具有最优子结构性质！
算法描述：采用贪心算法求解
贪心选择策略：重量最轻者先装船
根据以上分析：由此可产生该装载问题的最优解

void loading(int x[],  int w[], int c, int n) {
      int *R = (int *)malloc((n+1)*sizeof(int));
      // 根据w从小到大排序，数组R记录调整后的序号
      sort(w, R, n);  
      for (int i = 1; i <= n; i++) x[i] = 0;
      for (int i = 1; i <= n; i++) {
            int id = R[i]; 
            if (w[id] > c) break;
            x[id] = 1;  c -= w[id];
      }
}

题目2.活动安排问题
有n个活动的集合E={1,2,…,n}，其中每个活动都要求竞争使用同一资源，而在同一时间内只有一个活动能使用这一资源，每个活动 i 都有一个请求使用该资源的起始时间 si 和一个使用资源的结束时间 fi，且 si < fi 。如果选择了活动 i，则它在半开时间区间[si, fi)内占用资源，若区间[si, fi)与[sj, fj)不相交，则称活动i与活动j是相容的。如何选出最大的相容活动子集合。

贪心思想：
证明进行贪心选择可得全局最优解
首先证明活动安排问题有一个最优解以贪心选择开始
设：E={1，…，n}为给定活动集合（按结束时间由早到晚排列）
显然活动1具有最早的完成时间
设：集合A是该问题的一个最优解（按结束时间由早到晚排列）
不妨设A中的第一个活动是活动k
若k=1，则：A就是一个以贪心选择开始的最优解
若k>1，则设：B=(A-{k})∪{1}
由于F[1]≤F[k]，且A中活动相容，故B中活动也相容
由于B和A中包含的活动个数相同，故B也是最优的
得证：总存在一个以贪心选择开始的最优活动安排方案
选择活动1后
原问题就简化为对E中所有与活动1相容的活动进行活动安排的子问题。
可见每一步所做的贪心选择都将问题简化为一个更小的与原问题具有相同形式的子问题。

具体实现：
优先选择最先结束的活动，然后检测剩余活动中开始时间在剩余时间段中的最先结束的活动是否与已有活动冲突，如不冲突则加入选择，循环到没有活动为止。
这种选择方式为后序活动预留尽可能多的时间，贪心选择的意义在于：使剩余的可安排时间段极大化，以便安排尽可能多的相容活动

int Selector(vector<int>& start, vector<int>& finish, vector<boolean>& a)
{
	int n=start.length-1;
	a[1]=true;
	int j=1;
	int count=1;
	for(int i=2;i<=n;i++){
		if(start[i]>=finish[j]){
		a[i]=true;
		j=i;
		count++;
		}
		else a[i]=false;
		}
		
		return count;
}

题目3.背包问题
0-1背包问题：
给定n种物品和一个背包，背包的容量为C
设物品i的重量是W[i]，其价值为V[i] 。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
限制条件：在选择装入背包的物品时，对每种物品i只有2种选择，即装入背包或不装入背包；不能将物品 i 装入背包多次，也不能只装入部分的物品 i 。（因此称为0/1背包问题）
背包问题:
与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品 i 的一部分，而不一定要全部装入背包
这两类问题都具有相似的最优子结构性质，但背包问题可以用贪心算法求解，而0-1背包问题却不能用贪心算法求解！
两种背包问题的形式化表达：
0/1背包问题：
给定：c>0, wi>0, vi>0, 1≤i≤n
要求找出一个n元0/1向量(x1, x2,…, xn)
满足：$\sum _{i=1}^n{w}_i{x}_i\le c$ ($x_i$∈{0,1})
使得下式最大化：$\sum _{i=1}^n{v}_i{x}_i$

背包问题:
给定：c>0, wi>0, vi>0, 1≤i≤n
要求找出一个n元向量(x1, x2,…, xn)
满足：$\sum _{i=1}^n{w}_i{x}_i\le c$ ($0\le x_i\le 1$)
使得下式最大化：$\sum _{i=1}^n{v}_i{x}_i$
贪心算法求解背包问题的基本步骤：
首先计算每种物品单位重量的价值：vi/wi
然后按照贪心选择策略
将尽可能多的单位重量价值最高的物品装入背包
若将这种物品全部装入后，背包内的物品总重量未超过C
则选择单位重量价值次高的物品并尽可能多地装入背包
依此策略一直地进行下去，直到背包装满为止

例子
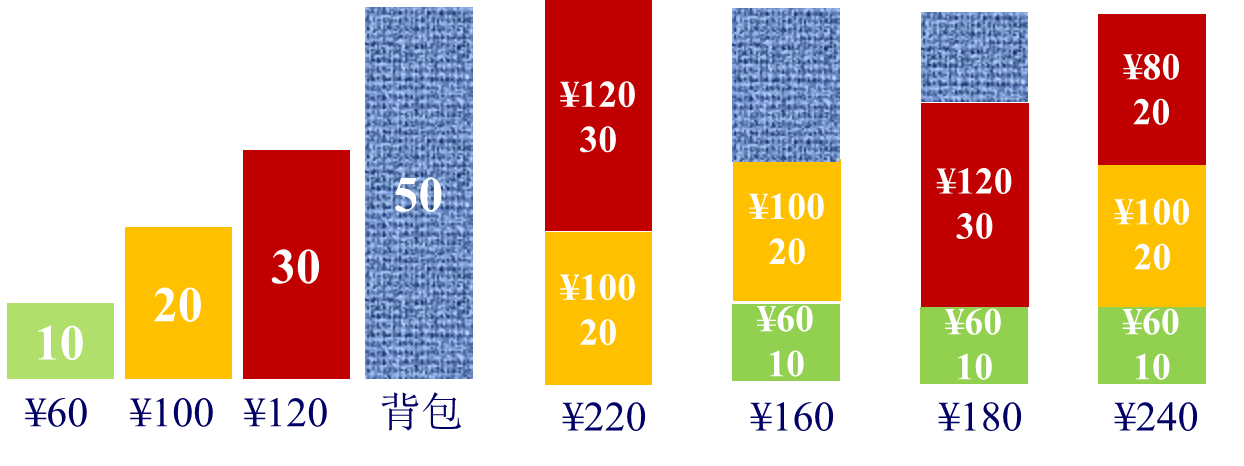
总共3件物品，背包容量50磅。物品1重10磅，价值60元，物品2重20磅，价值100元，物品3重30磅，价值120元。

物品1每磅价值6元，大于物品2的每磅价值5元和物品3的每磅价值4元。
对0-1背包问题，按照贪心策略的话就要物品1。然而从图中看出，最优解取的是物品2和3。选择物品1的可能解都是次优的。
对背包问题，选择物品1可以达到最优。

贪心算法与动态规划的区别

动态规划算法
每一步的最优解是由上一步的局部最优解进行选择得到的
因此需要保存（之前求解的）所有子问题的最优解备查
贪心算法
贪心策略：下一步的最优解是由上一步的最优解推导得到的
当前最优解包含上一步的最优解，之前的最优解则不作保留
因此在贪心算法中作出的每步决策都无法改变（不能回退）
二者关系
贪心算法本质上是一种（更快的）动态规划算法
贪心法正确的条件：每一步的最优解一定包含上一步的最优解
如果可以证明：在递归求解的每一步，按贪心选择策略选出的局部最优解，最终可导致全局最优解，则二者是等价的，这时用贪心算法更快更简单。