编译器-NFA转DFA

NFA 转 DAF ： subset construction（子集构造法）

对于一个正则表达式，虽然说NFA和DFA从input state走到final state总是能满足正则表达式的要求，但是NFA对于一个特定的例子可以有无限多中走法，而DFA对于一个特定的例子只有唯一的走法，所以DFA更利于编程转换成代码

转换的核心思想就是把NFA路线中的多个可能性的选择合并看作一个DFA state

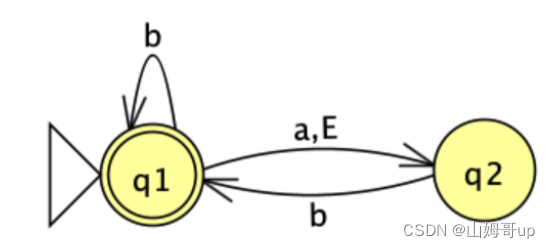
q1 → d1
q2 → d2
(q1,q2) → d3
∅ → d4

可以看出NFA的2个state可以最多有4个DFA state

如果有3个NFA state 那么可以最多有8个DFA state 即：{q1,q2,q3}
{q1}        {q2}        {q3}        {q1,q2}        {q1,q3}        {q2,q3}        {q1,q2,q3}        {∅}
可以看出 这八个DFA state都是{q1,q2,q3}的子集 所以这也是为什么叫subset construction

总结 如果有n个NFA state 那么可以有至多个DFA state

接下来看具体转换过程