Tree | 二叉查找树 —— 建立、查找、删除、懒惰删除

本文目录

一、二叉查找树的基本概念

二、二叉查找树的建立

1、二叉查找树的结构

2、二叉查找树的建立

 

三、二叉查找树的其他操作

1、查找元素

2、查找最小元素

3、查找最大元素

4、删除元素

四、一点补充

懒惰删除（Lazy Deletion）：

---

一、二叉查找树的基本概念

二叉查找树是一种特殊的二叉树，在查找的应用中很重要。

其在二叉树的基础上有如下规定：

对于树中的每一个节点数据key，其左儿子一定比key小，右儿子一定比key大。

并且对于一般的二叉查找树我们有如下约定：

1、数据域均为整型

2、数据不重复

进一步认识二叉树：

1、二叉查找树中每一棵子树都仍是二叉查找树。 

2、将二叉查找树从上向下压瘪了，成为一维排列——是一个增序排列。

二、二叉查找树的建立

1、二叉查找树的结构

二叉查找树本质是二叉树，所以其结构与二叉树相同。

有三个域：数据域、左孩子指针域、右孩子指针域。

结构体代码如下： 

typedef struct SearchTreeNode {
    int data;
    struct SearchTreeNode * left;
    struct SearchTreeNode * right;
} *SEARCH_TREE, search_tree;

2、二叉查找树的建立

二叉树的建立，可以通过插入函数来完成。将节点一个个正确恰当地插入根节点之下，即完成了整个二叉查找树的建立。

插入时，要考虑到根据二叉树的特性：树中的每一个节点数据key，其左儿子一定比key小，右儿子一定比key大。

插入函数很好理解：

1、有向遍历节点：向着正确的插入位置遍历。

即遍历到树的某一节点时，如果待插入数据比它小，我们就向着其左子树遍历，反之向其右子树遍历。显然，遍历的尽头就是空节点。

2、插入：我们始终将x插入到已有树的尽头。

即当遍历到NULL时，申请节点存入待插入数据，然后替代NULL。

下图展示了插入的具体过程：

代码实现： 

/* 传入参数为：
 * 待插入节点数据x、插入的树的根节点
 * 返回：
 * 插入位置的父节点 */
SEARCH_TREE Insert(int x, SEARCH_TREE T) {

    //递归的尽头：已经到了叶子节点之下
    if(!T) {
        T = (SEARCH_TREE)malloc(sizeof(search_tree));
        T->data = x;
        T->left = T->right = NULL;
    }
    //比当前节点小,向左搜寻插入位置
    else if (x < T->data)
        T->left = Insert(x, T->left);
    //比当前节点大,向右搜寻插入位置
    else if(x > T->data)
        T->right = Insert(x, T->right);
    return T;  //返回已经插入完毕的树
}

值得注意的是：以上插入函数，对于已有的元素继续插入，会直接返回，不进行插入操作。

 

三、二叉查找树的其他操作

1、查找元素

利用二叉查找树的性质，从树的根节点开始，比其大，继续查找其右子树；比其小，继续查找其左子树。

是一个递归的过程：

/* 传入参数为：
 * 待查找节点数据x、二叉查找树的根节点
 * 返回：
 * 如果找到，返回数据的节点;否则返回NULL */
SEARCH_TREE Find(int x, SEARCH_TREE root) {
    
    if(!root)  //查找到空树（说明树中没有待查找的节点）
        return NULL;
    
    if(x < root->data) //比当前节点小
        return Find(x, root->left);  //向左查找
    else if(x > root->data)//比当前节点大 
        return Find(x, root->right);  //向右查找
    else
        return root; //返回找到的节点
}

2、查找最小元素

二叉查找树十分方便查找，根据其定义，我们可以确定：树内最小元素在其最左端。

迭代法：只需要一直向其左子树搜寻，直到其左子树为空时，就是这棵二叉查找树的最小元素。

/* 传入参数为：
 * 二叉查找树
 * 返回：
 * 如果树不为空，返回最小节点;否则返回NULL */
SEARCH_TREE FindMin(SEARCH_TREE T) {
    //不是空树
    if (T) {
        while (T->left)  //当左子树不为空
            FindMin(T->left);  //一直向左搜寻
    }
    return T;
}

3、查找最大元素

同上，根据其定义，我们可以确定：树内最大元素在其最右端。

迭代法：只需要一直向其右子树搜寻，直到其右子树为空时，就是这棵二叉查找树的最大元素。

/* 传入参数为：
 * 二叉查找树
 * 返回：
 * 如果树不为空，返回最大节点;否则返回NULL */
SEARCH_TREE FindMax(SEARCH_TREE T) {
    //不是空树
    if (T) {
        while (T->right)  //当右子树不为空
            FindMax(T->right);  //一直向右搜寻
    }
    return T;
}

4、删除元素

 二叉查找树的删除操作相对来说复杂一点，我们必须保证在删除后不破坏二叉查找树树的性质。

我们将待删除的节点记为T，其情况有以下三种：

1、T没有子树

那么我们直接删除节点T就行，具体操作就是用NULL代替T，或者说free掉T。 

 

2、T有且仅有一棵子树

直接用T唯一的子树代替 T。

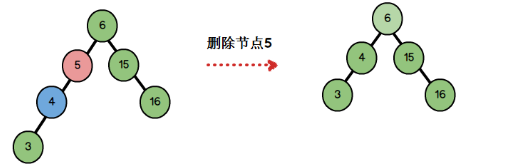
3、T有两棵子树

为了不改变二叉查找树的性质，我们可以选取T的左子树中的最大元素 / 右子树中的最小元素temp取代T，再删除temp原来所在的节点。

temp节点很好找，可利用上面已经实现的FindMax或FindMin函数。

 

理解了上图以后，再看代码就很简单啦~ 

/* 传入参数为：
 * 待删除元素x,二叉查找树
 * 返回：
 * 删除后的二叉查找树根节点 */
SEARCH_TREE Delete(int x, SEARCH_TREE T) {
    SEARCH_TREE temp;

    /* 寻找待删除节点 */
    if (x < T->data)
        T->left = Delete(x, T->left);  //向左子树中查找
    else if (x > T->data)
        T->right = Delete(x, T->right); //向右子树中查找
    /* 找到 T即为待删除节点 */
    else {
        //有两棵子树
        if(T->left && T->right) {
            temp = FindMin(T->right);  //找到待删除节点左子树中的最小元素temp
            T->data = temp->data;   //temp取代T
            T->right = Delete(temp->data, T->right); //删除temp原来节点
        }
        //有且仅有一棵子树或没有子树
        else {
            temp = T;
            if(!T->left)
                T = T->right;  //用右子树代替T
            else if (!T->right)
                T = T->left;  //用左子树代替
            free(temp);    
        }

        return T;
    }
}

 

四、一点补充

懒惰删除（Lazy Deletion）：

上面对于二叉树的删除操作有点麻烦，其实我们可以采取懒惰删除法，简单直观且不耗费时间。

懒惰删除，简单来说就是当要删除某节点N时，我们不直接实质地去删除它，而是用一个变量标记N为已删除状态。之后再用到这棵二叉树时，默认不访问被标记的“已删除节点”即可。这样操作的效果，一般情况下和真实地去删除一个节点是一样的。

至于如何标记，可以将节点的结构中再添加一个域——flag，标记其是否被删除即可。

---

---

---

End

欢迎关注个人公众号“鸡翅编程”，这里是认真且乖巧的码农一枚，旨在用心写好每一篇文章，平常会把笔记汇总成推送更新~