问题
四皇后问题是一张四乘四的棋盘,在棋盘中放四颗棋子,要求如下:任意两个皇后都不能处在同一行、同一列 任意两个皇后都不能处在同一斜线上(主斜线、反斜线)。
四皇后是八皇后的衍生版本,其原理都是一样的。八皇后说的是在8×8的国际棋盘上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?八皇后一共有92种解法。而四皇后是在一个4×4的棋盘上摆放4个皇后。
要求
- 任意两个皇后都不能处在同一行、同一列
- 任意两个皇后都不能处在同一斜线上(主斜线、反斜线)
思路
- 定义一个数组a[20],a[i]=j表示第i个皇后放在第i行第j列。
- 函数issafe()用于判断当前位置是否可选(在同一列、同一斜线,返回0;否则,返回1,表示可选
- 函数search()用于输出结果并判断,用到了递归中的回溯法。

算法
#include<iostream>
using namespace std;
int a[20]={-1},flag=0,count=0;//判断当前位置是否可选(在同一列、同一斜线,返回0;否则,返回1,表示可选
int issafe(int row,int col)//row表示当前将要选的行,cow表示当前将要选的列
{
for(int k=0;k<row;k++) //遍历前面放置了皇后的行
{
if(a[k]==col) return 0; //同一列不安全
if(row-k==col-a[k]) return 0; //同一主对角线,行之差和列之差相等
if((row-k)+(col-a[k])==0) return 0;//副对角线,行之差列之差互为相反数,即和为0
}
return 1;
}void search(int i,int n)
{ if(i-1==n-1&&flag)
{
++count;
for(int t=0;t<n;t++)
cout<<a[t]<<' ';
cout<<endl;
return ; //结束 ,退出本层
}
else
{
for(int j=0;j<n;j++) //回溯法,j不能定义为全局变量,否则用过会保存当前值,不会返回上层j+1的值,只能定义为局部变量
{
//cout<<i<<' '<<j<<endl;
if(issafe(i,j))
{
a[i]=j;
flag=issafe(i,j);
search(i+1,n);
}
}
i--; //回溯法,返回上层
}
}int main()
{
int n;
cin>>n;
search(0,n);
cout<<count<<endl;
}结果
四皇后
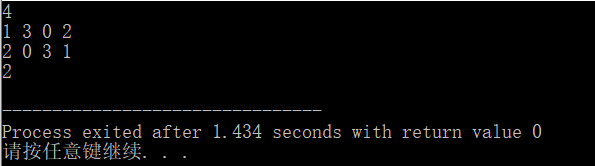
执行过程


八皇后结果
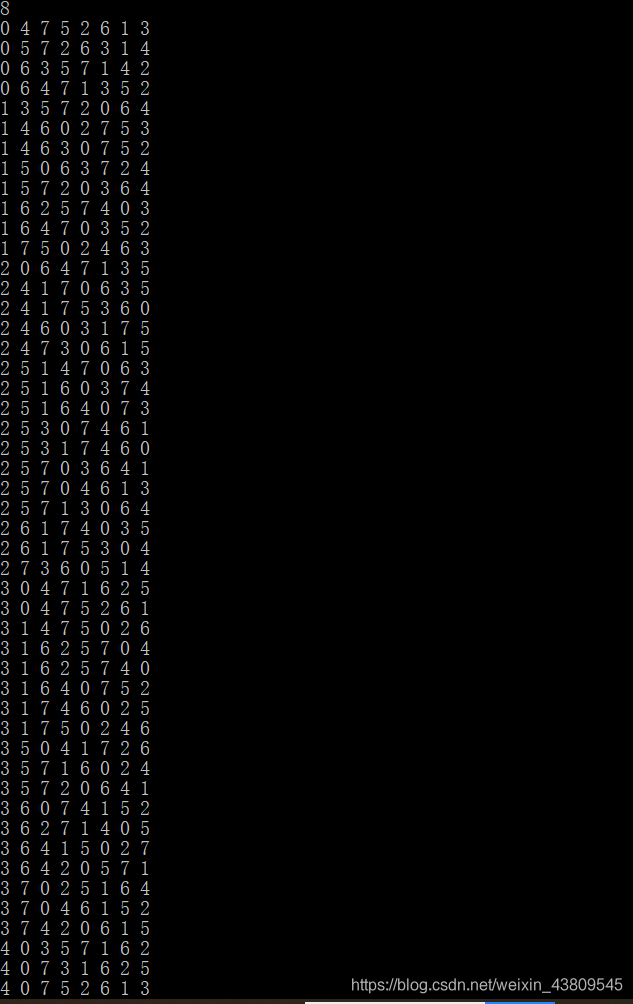

























 5090
5090

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








