如何找到与证明素数之一：小素数和概率素数的快速检验

引言

在前一篇文章中，我们对如何寻找素数给出了三类方法，本文则详细讨论前篇文章的第一节内容。首先是一个简短的介绍和目录。本章讨论寻找小素数和基本的概率素性检验。

---

一、寻找十分小的素数

为了找到所有的小素数，比如小于 $10,000,000,000$ 的素数，最有效的方法之一是使用埃拉托色尼筛法 ( 公元前 240 年 )：

列出所有小于或等于 $n$ ( 大于 $1$ ) 的整数，去掉所有小于或等于根号 $n$ 的素数的倍数，剩下的数就是素数。

例如，要找出所有小于或等于 $100$ 的奇素数，我们首先列出从 $3$ 到 $100$ 的奇数，第一个数是 $3$，所以它是第一个奇素数，把它的倍数都划掉。剩下的第一个数是 $5$，即第二个奇素数，把它的倍数都划掉。重复到 $7$ 后，因为剩下的第一个数 $11$ 大于 $100$ 的平方根，所以剩下的所有数都是素数。

这种方法非常快，以至于没有理由在计算机上存储大量的素数列表——如此高效的实现可以比计算机从磁盘读取素数的速度更快地找到它们。

Bressoud 有这个算法的伪代码实现 [Factorizations and primality testing, 1989, p19]，Riesel 有一个 PASCAL 实现 [Prime numbers and computer methods for factorization, 1994, p6]。也可以基于二次形创建更快的筛法。

如果找小素数，试除法效果会很好。要检验 $n$ 是否是素数，只需除以所有小于 $\sqrt{n}$ 的素数。例如，要验证 $211$ 是不是素数，只需除以 $2、3、5、7、11$ 和 $13$ 。( 伪代码 [Bressoud, Factorizations and primality testing, pp 21-22]， PASCAL [Prime numbers and computer methods for factorization, pp 7-8] )。有时数字 $n$ 的形式使这种方法特别有效 ( 例如，梅森数的因子有一种特殊的形式 )。

与其只除以素数，有时除以 $2,3$ 和 $5$ 更实用；然后除以对 $30(=2\cdot 3\cdot 5)$ 取模等于：
$$1,7,11,13,17,19,23,29$$的所有整数，同样在取到平方根时停止。这种类型的分解有时称为轮式分解 ( wheel factorization )。它需要更多的除法 ( 因为一些除数是合数 )，但不需要我们有一个可用的素数列表。我们将模 $30$ 的余数 $1,7,11,13,17,19,23,29$ 称为轮辐 ( spokes ) 。

例如我们要用上面提到的轮式分解来判断 $3331$ 是否是素数，我们要除以 $2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、49$ 和 $53$ 。注意 $49$ 不是素数，但相对于轮式分解来说是素数 ( 不妨称这组数为轮式分解素数 ) 。前面的 $2,3,5$ 是 $30$ 的因数，需要人为添上。

轮式分解其实是一种特殊类型的筛法。

轮 ( wheels ) 可以做成任何尺寸。最简单的轮是用一个素数 $2$ 来创造的，同时有一条轮辐：$1$ ( 所以我们要除以 $2$ ，然后取每个奇数 )。稍微复杂一点的轮会使用素数 $2$ 和 $3$ 。这样我们就有了两条轮辐：1 和 5 ( 模 $6$ 的余数，因 $2,3$ 被用到，故此处不能出现 ) 。所以我们要除以下面的整数：
$$2,3,5,7,11,13,17,19,23,25,29,31,35,37,41,43,\cdots$$ 前面的 $2,3$ 是 $6$ 的因数，需要人为添上。

这与将整数写在宽度为 $6$ 的表中是一样的——所有素数 ( 除了 $2$ 或 $3$ ) 最后都在与两个轮辐 $1$ 和 $5$ 对应的列中。( 素数用绿色表示 )

如果我们从素数 $2,3,5,7$ 开始，然后检查对 210 ( 这四个素数的乘积 ) 取模的余数是否与如下轮辐一致：

1, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 121, 127, 131, 137, 139, 143, 149, 151, 157, 163, 167, 169, 173, 179, 181, 187, 191, 193, 197, 199, 209. ( 121, 143, 169, 187, 209 为真正意义的合数 )

请注意，除了 $1$ 之外，轮中这些最小的轮辐都是素数 ( 轮式分解素数 ) 。这是因为任何小于轮中使用的最大素数的平方的数，都必须是素数，而不是轮所除去的 ( 轮中使用的数是指一个整数 $n$ 除以轮辐中其平方小于 $n$ 的那些轮辐 )。然而这也误导过许多人，认为这样的轮是素数的良好“生成器”。但事实并非如此，素数的密度会随着整数大小的增加而减小 ( 参见素数定理 )，因此当我们将这些相同的轮应用于一个大的整数列表时，几乎所有没有被轮排除的数都是合数。

基于 $2$ 和 $3$ 的简单轮排除了 $4/6=2/3$ 的合数。使用 $2、3、5$ 和 $7$ 的较复杂轮将去除 $162/210$ ( 超过 $77\%$ ) 的合数。

复杂轮的效率不是特别高。要去除 $90\%$ 的合数，我们必须使用 $251$ 以内的素数。$95\%$ 要求素数直到 $75037$。$96\%$ 要求素数直到 $1246379$ 。$97\%$ 要求素数直到 $134253593$ ！想象一下，你需要多少素数才能去除 $99\%$ 的合数！这个模数又会是多么巨大！

假设整数 $n$ 超过 $25$ 位，那么除以小于其平方根的轮式分解素数是不切实际的。如果 $n$ 有 $200$ 位，那么试除法是不可行的——所以需要更快的素性检验。我们将在下面讨论几个这样的检验。

---

二、费马数，概率素数和伪素数

费马大定理，也是他的“最后”定理，说明了当 $n\ge 2$ 时，丢番图方程 $x^n+y^n=z^n$ 无正整数 $x,y,z$ 解。 这最终被 Wiles 于 1995 年证明。此处我们关注的是他的“小”定理：

费马小定理    \; 若 $p$ 是素数，$a$ 是任一整数，则 $a^p\equiv a(modp)$ ；特别地，若 $p\nmid a$ ，则 $a^{p-1}\equiv 1(modp)$ 。

费马小定理给了我们一个强大的合数性检验：给定 $n>1$、选择 $a>1$ ，并计算 $a^{n-1}$ 模 $n$ ( 有一种非常简单的方法叫快速幂或二进制幂 ( binary exponentiation ) ，通过重复平方来快速完成 ) 。如果结果不是模 $n$ 余 $1$ ，那么 $n$ 是合数。如果是模 $n$ 余 $1$ ，那么 $n$ 可能是素数，所以 $n$ 被称为基于 $a$ 的弱概率素数 ( 或 a-PRP ) 。

一些早期文献把满足这个检验的所有数都称为伪素数，但是现在伪素数这个术语被适当地保留给合数概率素数。

伪素数 ( 合数 PRPs ) 的最小示例如下。

• $341=11\cdot 31$ 是一个 2-PRP, (Sarrus 1819) ,
• $91=7\cdot 13$ 是一个 3-PRP ,
• $217=7\cdot 31$ 是一个 5-PRP ,
• $25=5\cdot 5$ 是一个 7-PRP .

虽然有 $1,091,987,405$ 个素数小于 $25,000,000,000$ ，但其中只有 $21,853$ 个以 $2$ 为基数的伪素数，所以 Henri Cohen 开玩笑说 2-PRP 是工业级素数。幸运的是，$n$ 越大，PRP 检验正确的可能性 ( 平均而言 ) 就越大——请参阅下图。

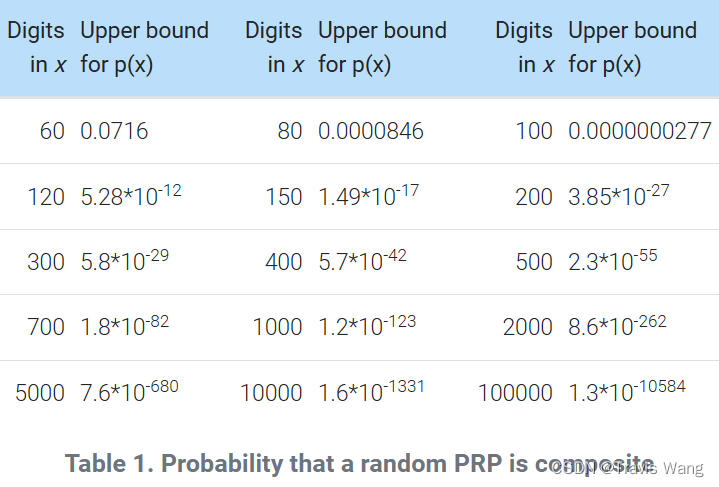
有趣的是，早在 1950 年，Lehmer 使用概率 / 伪素数的较弱定义 $a^n\equiv a(modn)$，发现 $2\cdot 73\cdot 1103=161038$ 是一个以 $2$ 为基底的偶伪素数。理查德·平奇在他的网站上列出了直到 $10^{21}$ ( 根据各种定义 ) 的伪素数。

伪素数可能相对较少，但对于每一个基数 $a>1$ ，伪素数仍然有无穷多，所以我们需要一个更严格的测试。使测试更准确的一种方法是使用多个基底 ( 检查以 $2$ 为基底，然后以 $3$ 为基底，然后以 $5$ 为基底，… )，但我们仍然遇到了一个有趣的障碍，叫做卡迈克尔数 ( Carmichael numbers ) 。

定义    \; 合数 $n$ 是一个卡迈克尔数，如果 $a^{n-1}\equiv 1(modn)$ 对任意与 $n$ 互素的 $a$ 都成立。

这里有一个坏消息：对一个卡迈克尔数的反复 $PRP$ 检验将无法表明它是合数，直到我们找到它的一个因子。虽然卡迈克尔数是罕见的 ( 只有 $2163$ 个小于 $25,000,000,000$ )，但最近已经证明存在无限多个 [There are infinitely many Carmichael numbers, 1994] 。卡迈克尔数小于 $10$ 万的部分如下 ( 共 $16$ 个 )：

561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361.

理查德·平奇将卡迈克尔数列到了 $10^{16}$ 。

备注：Jon Grantham 提出了 Frobenius 伪素数的想法，以推广许多标准类型 ( Fermat, Lucas… )，并使检验更准确。他的论文可以在网上找到。

---

三、强概率素性检验

使费马检验更准确的一个更好的方法是：如果奇数 $n$ 是素数，那么数字 $1$ 只有两个平方根 $1$ 和 $-1$ 模 $n$ 。所以 $a(n-1)/2$ ( 因为 $n$ 是奇数 ) 模 $n$ 等于 $1$ 或 $-1$ 。( 实际上可以用雅可比符号来计算它应该是哪个，但我们希望在这里开发一个更强大的检验 ) 。 如果 $(n-1)/2$ 是偶数，我们可以很容易地再取一个平方根 …… 让我们把它变成一个算法：

记 $n-1=2^s\cdot d$ ，其中 $d$ 是奇数且 $s$ 非负：$n$ 是一个基于 $a$ 的强概率素数 ( a-SPRP )，如果对于某些非负数 $r\le s$ 有 $a^d\equiv 1(modn)$ 或者 $(a^d{)}^{2^r}\equiv -1(modn)$ 这两者之一成立。

同样，所有整数 $n>1$ 若未通过此检验的，为合数；通过检验的是概率素数。最小的奇合数 SPRP 如下：

• $2047=23\cdot 89$ 是一个 2-SPRP,
• $121=11\cdot 11$ 是一个 3-SPRP,
• $781=11\cdot 71$ 是一个 5-SPRP,
• $25=5\cdot 5$ 是一个 7-SPRP.

基于这些结果的检验非常快，特别是结合前几个素数使用的试除法。如果你在编写这些程序时遇到困难，Riesel [Prime numbers and computer methods for factorization, p100] 有用于 SPRP 测试的 PASCAL 代码，Bressoud 有伪代码[Factorizations and primality testing, p77]， Langlois 提供 C 语言代码。

单独来说，这些测试仍然很弱 ( 每个基数 $a>1$ 都有无穷多个合数 a-SPRP )，但我们可以将这些单独的检验结合起来，对小整数 $n$ 进行更强大的检验：

• 如果 $n<1,373,653$ 既是 2-SPRP 也是 3-SPRP，那么 $n$ 是素数，
• 如果 $n<25,326,001$ 既是 2-SPRP、3-SPRP 也是 5-SPRP，那么 $n$ 是素数，
• 如果 $n<118,670,087,467$ 既是 2-SPRP、3-SPRP、5-SPRP 也是 7-SPRP，则要么 $n=3,215,031,751$ ，要么 $n$ 是素数，
• 如果 $n<2,152,302,898,747$ 既是 2-SPRP、3-SPRP、5-SPRP、7-SPRP 也是 11-SPRP，那么 $n$ 是素数，
• 如果 $n<3,474,749,660,383$ 既是 2-SPRP、3-SPRP、5-SPRP、7-SPRP、11-SPRP 也是 13-SPRP，那么 $n$ 是素数，
• 如果 $n<341,550,071,728,321$ 既是 2-SPRP、3-SPRP、5-SPRP、7-SPRP、11-SPRP、13-SPRP 也是 17-SPRP，那么 $n$ 是素数。

要根据这些结果快速进行素性检验，首先除以前几个素数 ( 比如低于 $257$ 的素数 )，然后执行以 $2,3,\cdots$ 为基数的强素性检验直到满足上述条件之一。例如，如果 $n<25,326,001$ ，我们只需要检查基数 $2,3$ 和 $5$ 。这比试除法快得多，因为别人已经做了很多工作，但只适用于很小的数字 ( $n<10^{16}$ ) 。

请注意，可以通过不将它们作为单独的检验来加强这些结果，而是意识到我们正在寻找 $-1$ 的平方根。例如，$n=46,856,248,255,981$ 是 $2$-伪素数 和 $7$-伪素数，但是
$$2^{(n-1)/4}\equiv 34456063004337(modn),$$ $$7^{(n-1)/4}\equiv 21307242304265(modn).$$ 以上这两个的平方是 $-1$ 。如果 $n$ 是素数，那么它就只有两个平方根，并且上面的数是相等的或者是相反的 ( 显然两者皆不满足 ) 。然而 $\gcd (n,34456063004337-21307242304265)=4840261$，我们便已经分解了 $n$ 。

最后，还有很多可以 ( 也应该 ) 说的。我们可以讨论欧拉伪素数及其与 SPRP 的关系。或者我们可以换一下：讨论卢卡斯伪素数，或斐波那契伪素数，或重要的组合检验 …… 但这需要一本书的一章——而 Ribenboim [The new book of prime number records, 1995] 的书已经写得很好了。让我们以最后一个结果来结束本节：

米勒检验 ( Miller’s Test )：如果广义黎曼假设成立，那么当 $n$ 是所有整数 a 的 a-SPRP ( 其中 $1<a<2(\log (n){)}^2$ ) ，则 $n$ 是素数。

广义黎曼假设对我们来说太复杂了，无法在这里解释——但如果它被证明了，那么我们就有了一个非常简单的素性检验。在它被证明之前，我们至少可以期望，如果 $n$ 是合数，我们应该能够找到一个表明它是合数的 a ( 一个见证者 )，而不用搜索太长时间。

大多数研究涵盖了米勒检验 ( 通常使用常数 a=$70$，来自文献 [Oesterlé, Versions effectives du théorème de chebotarev sous l’hypothèse de riemann généralisée, 1979]，正如米勒的文章所说的 $O((logn{)}^2)$ ) 。可改进常数 a=$2$ 是由 Bach 在文章 [Analytic methods in the analysis and design of number-theoretic algorithms, 1985] 中提出的。请注意，启发式地 Bach 和Huelsbergen [Statistical evidence for small generating sets, 1993] 认为我们应该能够用更小的边界替换 Miller 检验中的边界：
$$(\log 2{)}^{-1}\log n\log \log n.$$ 请注意，在米勒检验中没有有限的基数集合。事实上，如果 $n$ 是合数，我们让 $W(n)$ 表示 $n$ 的最小见证者 ( 最小 $a$ 表明 $n$ 是合数 )，那么有无穷多的合数 $n$ 满足：
$$W(n)>(\log n{)}^{1/(3\log \log \log n)}$$ 上述结论参见 [There are infinitely many Carmichael numbers, 1994] 。

译者补充：米勒检验已经改进为目前常见的 Miller-Rabin 检验，不再依赖广义黎曼假设，该检验详细参考此处。