灰色预测模型
灰色预测是对既含有已知信息又含有不确定信息的系统进行预测,就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
灰色预测对原始数据进行生成处理来寻找系统变动的规律,并生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
一、GM(1,1)模型简介
GM(1,1)是最简单的灰色预测模型,它是使用原始的离散非负数据列,通过一次累加生成削弱随机性的较有规律的新的离散数据列,然后通过建立微分方程模型,得到在离散点处的解经过累减生成的原始数据的近似估计值,从而预测原始数据的后续发展。(本文中只探究 GM(1,1) 模型,第一个 1 表示微分方程是一阶的,后面的 1 表示只有一个变量)
二、GM(1,1)原理
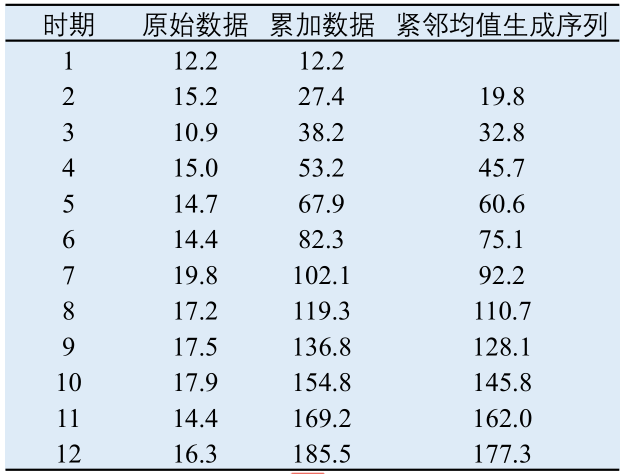
设 x ( 0 ) = ( x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) , ⋯ , x ( 0 ) ( n ) ) x^{(0)}=(x^{(0)}(1),x^{(0)}(2),\cdots,x^{(0)}(n)) x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n)) 是最初非负数据列,对其一次累加得到新的生成数据 x ( 1 ) x^{(1)} x(1) 。
x ( 1 ) = ( x ( 1 ) ( 1 ) , x ( 1 ) ( 2 ) , ⋯ , x ( 1 ) ( n ) ) x^{(1)}=(x^{(1)}(1),x^{(1)}(2),\cdots,x^{(1)}(n)) x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n)),其中: x ( 1 ) ( m ) = ∑ i = 1 m x ( 0 ) ( i ) , m = 1 , 2 , ⋯ , n x^{(1)}(m)=\sum_{i=1}^{m}{x^{(0)}(i)},m=1,2,\cdots,n x(1)(m)=∑i=1mx(0)(i),m=1,2,⋯,n。
令
z
(
1
)
z^{(1)}
z(1) 为数列
x
(
1
)
x^{(1)}
x(1) 的紧邻生成数列,即
z
(
1
)
=
(
z
(
1
)
(
1
)
,
z
(
1
)
(
2
)
,
⋯
,
z
(
1
)
(
n
)
)
z^{(1)}=(z^{(1)}(1),z^{(1)}(2),\cdots,z^{(1)}(n))
z(1)=(z(1)(1),z(1)(2),⋯,z(1)(n)),其中:
z
(
1
)
(
m
)
=
δ
x
(
1
)
(
m
)
+
(
1
−
δ
)
x
(
1
)
(
m
−
1
)
,
m
=
2
,
3
,
⋯
z^{(1)}(m)=\delta x^{(1)}(m)+(1-\delta)x^{(1)}(m-1),m=2,3,\cdots
z(1)(m)=δx(1)(m)+(1−δ)x(1)(m−1),m=2,3,⋯,
n
n
n 且
δ
=
0.5
\delta =0.5
δ=0.5。

我们称方程 x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b x^{(0)}(k)+az^{(1)}(k)=b x(0)(k)+az(1)(k)=b 为 GM(1,1) 模型的基本形式(k=2,3,…,n),其中, b b b 表示灰作用量。 − a -a −a 表示发展系数。下面引入矩阵形式:
u = ( a , b ) T , Y = [ x ( 0 ) ( 2 ) x ( 0 ) ( 3 ) ⋮ x ( 0 ) ( n ) ] , B = [ − z ( 1 ) ( 2 ) 1 − z ( 1 ) ( 3 ) 1 ⋮ ⋮ − z ( 1 ) ( n ) 1 ] u=(a,b)^T,\quad Y=\left[ \begin{array}{c} x^{(0)}(2)\\ x^{(0)}(3)\\ \vdots \\ x^{(0)}(n) \end{array}\right],\quad B=\left[ \begin{array}{c} -z^{(1)}(2)\quad 1\\ -z^{(1)}(3)\quad 1\\ \quad\vdots \quad\qquad \vdots \\ -z^{(1)}(n)\quad 1 \end{array}\right] u=(a,b)T,Y=⎣⎢⎢⎢⎡x(0)(2)x(0)(3)⋮x(0)(n)⎦⎥⎥⎥⎤,B=⎣⎢⎢⎢⎡−z(1)(2)1−z(1)(3)1⋮⋮−z(1)(n)1⎦⎥⎥⎥⎤
于是,GM(1,1) 模型
x
(
0
)
(
k
)
+
a
z
(
1
)
(
k
)
=
b
x^{(0)}(k)+az^{(1)}(k)=b
x(0)(k)+az(1)(k)=b 可表示为:
Y
=
B
u
\bf Y=Bu
Y=Bu
利用最小二乘法得到参数 a,b 的估计值为:
u
^
=
(
a
^
b
^
)
=
(
B
T
B
)
−
1
B
T
Y
\color{fuchsia}{ \hat u=\left( \begin{array}{c} \hat a\\ \hat b\\ \end{array} \right)=\bf (B^TB)^{-1}B^TY}
u^=(a^b^)=(BTB)−1BTY
实际上就是将
x
(
0
)
x^{(0)}
x(0) 序列视为因变量
y
y
y,
z
(
1
)
z^{(1)}
z(1) 序列是为自变量
x
x
x,进行回归。
x
(
0
)
(
k
)
=
−
a
z
(
1
)
(
k
)
+
b
⇒
y
=
k
x
+
b
\color{red}{\bf x^{(0)}(k)=-az^{(1)}(k)+b \quad\Rightarrow\quad y=kx+b}
x(0)(k)=−az(1)(k)+b⇒y=kx+b
引入最小二乘法(OLS)
最小二乘法定义:
y
i
^
=
k
x
i
+
b
,
k
^
,
b
^
=
a
r
g
min
k
,
b
(
∑
i
=
1
n
(
y
i
−
y
i
^
)
2
)
=
a
r
g
min
k
,
b
∑
i
=
1
n
(
y
i
−
k
x
i
−
b
)
2
\hat{y_i} =kx_i+b,\quad \hat{k},\hat{b}=\mathop{arg\min}\limits_{k,b}(\sum_{i=1}^{n} (y_i-\hat{y_i})^2)= \mathop{arg\min}\limits_{k,b} \sum_{i=1}^{n}{(y_i-kx_i-b)^2}
yi^=kxi+b,k^,b^=k,bargmin(i=1∑n(yi−yi^)2)=k,bargmini=1∑n(yi−kxi−b)2
我们令:
L
=
∑
i
=
1
n
(
y
i
−
k
x
i
−
b
)
2
=
[
y
1
−
k
x
1
−
b
,
y
2
−
k
x
2
−
b
,
⋯
,
y
n
−
k
x
n
−
b
]
[
y
1
−
k
x
1
−
b
y
2
−
k
x
2
−
b
⋮
y
n
−
k
x
n
−
b
]
L=\sum_{i=1}^{n}(y_i-kx_i-b)^2=[y_1-kx_1-b,y_2-kx_2-b,\cdots,y_n-kx_n-b] \left[ \begin{array}{c} y_1-kx_1-b\\ y_2-kx_2-b\\ \vdots\\ y_n-kx_n-b\\ \end{array} \right]
L=i=1∑n(yi−kxi−b)2=[y1−kx1−b,y2−kx2−b,⋯,yn−kxn−b]⎣⎢⎢⎢⎡y1−kx1−by2−kx2−b⋮yn−kxn−b⎦⎥⎥⎥⎤
并且令:
矩
阵
Y
=
[
y
1
y
2
⋮
y
n
]
,
X
=
[
1
x
1
1
x
2
⋮
⋮
1
x
n
]
,
β
=
[
b
k
]
矩阵 Y = \left[ \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n\\ \end{array} \right],\quad X=\left[ \begin{array}{c} 1 \quad x_1\\ 1 \quad x_2\\ \vdots \text{ }\quad\text{ }\vdots\\ 1 \quad x_n\\ \end{array} \right],\quad \beta= \left[ \begin{array}{c} b\\ k\\ \end{array} \right]
矩阵Y=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤,X=⎣⎢⎢⎢⎡1x11x2⋮ ⋮1xn⎦⎥⎥⎥⎤,β=[bk]
那么:
X
β
=
[
b
+
k
x
1
b
+
k
x
2
⋮
b
+
k
x
n
]
,
Y
−
X
β
=
[
y
1
−
k
x
1
−
b
y
2
−
k
x
2
−
b
⋮
y
n
−
k
x
n
−
b
]
X\beta=\left[ \begin{array}{c} b+kx_1\\ b+kx_2\\ \vdots\\ b+kx_n\\ \end{array} \right],\quad Y-X\beta=\left[ \begin{array}{c} y_1-kx_1-b\\ y_2-kx_2-b\\ \vdots\\ y_n-kx_n-b\\ \end{array} \right]
Xβ=⎣⎢⎢⎢⎡b+kx1b+kx2⋮b+kxn⎦⎥⎥⎥⎤,Y−Xβ=⎣⎢⎢⎢⎡y1−kx1−by2−kx2−b⋮yn−kxn−b⎦⎥⎥⎥⎤
所以有:
L
=
(
Y
−
X
β
)
T
(
Y
−
X
β
)
=
(
Y
T
−
β
T
X
T
)
(
Y
−
X
β
)
=
Y
T
Y
−
Y
T
X
β
−
β
T
X
T
Y
+
β
T
X
T
X
β
则
β
^
=
[
b
^
k
^
]
=
a
r
g
min
β
(
L
)
=
a
r
g
m
i
n
β
=
(
Y
T
Y
−
Y
T
X
β
−
β
T
X
T
Y
+
β
T
X
T
X
β
)
\begin{array}{l} L=(Y-X\beta)^T(Y-X\beta) \\ \quad=(Y^T-\beta^TX^T)(Y-X\beta)\\ \quad=Y^TY-Y^TX\beta-\beta^TX^TY+\beta^TX^TX\beta \\ \end{array}\\ 则 \text{ }\hat \beta=\left[ \begin{array}{c} \hat b\\ \hat k\\ \end{array} \right]=\mathop{arg\min}\limits_{\beta}{(L)}=\mathop{argmin}\limits_{\beta}=(Y^TY-Y^TX\beta-\beta^TX^TY+\beta^TX^TX\beta)\\
L=(Y−Xβ)T(Y−Xβ)=(YT−βTXT)(Y−Xβ)=YTY−YTXβ−βTXTY+βTXTXβ则 β^=[b^k^]=βargmin(L)=βargmin=(YTY−YTXβ−βTXTY+βTXTXβ)
对矩阵求导:
d
L
d
t
=
−
X
T
Y
−
X
T
Y
+
2
X
T
X
β
=
0
⇒
X
T
X
β
=
X
T
Y
\frac {dL}{dt}=-X^TY-X^TY+2X^TX\beta=0\Rightarrow X^TX\beta=X^TY\\
dtdL=−XTY−XTY+2XTXβ=0⇒XTXβ=XTY
所以:
β
^
=
(
X
T
X
)
−
1
X
T
Y
\color{fuchsia}{\bf\hat\beta=(X^TX)^{-1}X^TY}
β^=(XTX)−1XTY
最小二乘法可参考:https://blog.csdn.net/weixin_43819566/article/details/113091852
利用 OLS 估计的回归结果可以得出 a ^ \hat a a^ 和 b ^ \hat b b^,即 x ( 0 ) ( k ) = − a ^ z ( 1 ) ( k ) + b ^ ( k = 2 , 3 , ⋯ , n ) x^{(0)}{(k)}=-\hat az^{(1)}(k)+\hat b \quad (k=2,3,\cdots,n) x(0)(k)=−a^z(1)(k)+b^(k=2,3,⋯,n)
x ( 0 ) ( k ) = − a ^ z ( 1 ) ( k ) + b ^ ⇒ x ( 1 ) ( k ) − x ( 1 ) ( k − 1 ) = − a ^ z ( 1 ) ( k ) + b ^ x^{(0)}{(k)}=-\hat az^{(1)}(k)+\hat b \Rightarrow \color {blue} { x^{(1)}(k)-x^{(1)}(k-1) \color{black}{\text{ } = \text{ }-\hat a } \color{fuchsia}{ z^{(1)}(k)}} \color{black}{\text{ }+\text{ }} \color{red}{\hat b} x(0)(k)=−a^z(1)(k)+b^⇒x(1)(k)−x(1)(k−1) = −a^z(1)(k) + b^
对于以上式子:
等
式
左
边
:
x
(
1
)
(
k
)
−
x
(
1
)
(
k
−
1
)
=
∫
k
−
1
k
d
x
(
1
)
(
t
)
d
t
d
t
(
牛
顿
莱
布
尼
茨
公
式
)
等
式
右
边
:
z
(
1
)
(
k
)
=
x
(
1
)
(
k
)
+
x
(
1
)
(
k
−
1
)
2
≈
∫
k
−
1
k
x
(
1
)
(
t
)
d
t
(
定
积
分
几
何
意
义
)
等式左边:\color {blue} { x^{(1)}(k)-x^{(1)}(k-1)}\color{#000}{ = \int_{k-1}^k {\frac{dx^{(1)}(t)}{dt}} \,dt}\quad(牛顿莱布尼茨公式)\\ 等式右边:\color {fuchsia} {z^{(1)}(k)} \color {black} {\text{ } =\text{ } \frac{x^{(1)}(k)+x^{(1)}(k-1)}{2}}\approx \int_{k-1}^k x^{(1)}(t)dt\quad(定积分几何意义)
等式左边:x(1)(k)−x(1)(k−1)=∫k−1kdtdx(1)(t)dt(牛顿莱布尼茨公式)等式右边:z(1)(k) = 2x(1)(k)+x(1)(k−1)≈∫k−1kx(1)(t)dt(定积分几何意义)

∫ k − 1 k d x ( 1 ) ( t ) d t d t ≈ − a ^ ∫ k − 1 k x ( 1 ) ( t ) d t + ∫ k − 1 k b ^ d t = ∫ k − 1 k [ − a ^ x ( 1 ) ( t ) + b ^ ] d t \color{blue}{\int_{k-1}^k {\frac{dx^{(1)}(t)}{dt}} \,dt}\color{black}{\text{ }\approx\text{ }-\hat a}\color{fuchsia}{\int_{k-1}^k x^{(1)}(t)dt}\color{black}{\text{ }+\text{ }}\color{red}{\int_{k-1}^k \hat b dt}\color{black}{=\int_{k-1}^k\left[-\hat ax^{(1)}(t)+\hat b\right]}dt ∫k−1kdtdx(1)(t)dt ≈ −a^∫k−1kx(1)(t)dt + ∫k−1kb^dt=∫k−1k[−a^x(1)(t)+b^]dt
微 分 方 程 : d x ( 1 ) ( t ) d t = − a ^ x ( 1 ) ( t ) + b ^ 被 称 为 G M ( 1 , 1 ) 模 型 的 白 化 方 程 微分方程:\bf\frac{dx^{(1)}(t)}{dt}=-\hat ax^{(1)}(t)+\hat b\quad被称为\text{ }GM(1,1)\text{ }模型的白化方程 微分方程:dtdx(1)(t)=−a^x(1)(t)+b^被称为 GM(1,1) 模型的白化方程
x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b 被 称 为 G M ( 1 , 1 ) 的 灰 色 微 分 方 程 \bf x^{(0)}(k)+az^{(1)}(k)=b被称为\text{ }GM(1,1)\text{ }的灰色微分方程 x(0)(k)+az(1)(k)=b被称为 GM(1,1) 的灰色微分方程
白化方程求解:
白化方程:
d
x
(
1
)
(
t
)
d
t
=
−
a
^
x
(
1
)
(
t
)
+
b
^
\frac{dx^{(1)}(t)}{dt}=-\hat ax^{(1)}(t)+\hat b
dtdx(1)(t)=−a^x(1)(t)+b^,如果取初始值
x
^
(
1
)
(
t
)
∣
t
=
1
=
x
(
0
)
(
1
)
\hat x^{(1)}(t)\mid_{t=1}=x^{(0)}(1)
x^(1)(t)∣t=1=x(0)(1),可求出对应的解为:
x
(
1
)
(
t
)
=
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
(
t
−
1
)
+
b
^
a
^
所
以
x
(
1
)
(
m
+
1
)
=
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
(
m
)
+
b
^
a
^
,
m
=
1
,
2
,
⋯
,
n
−
1
x^{(1)}(t)=\left[ x^{(0)}(1)-\frac{\hat b}{\hat a}\right]e^{-\hat a(t-1)}+\frac{\hat b}{\hat a}\\ 所以\quad x^{(1)}(m+1)=\left[ x^{(0)}(1)-\frac{\hat b}{\hat a}\right]e^{-\hat a(m)}+\frac{\hat b}{\hat a},\quad m=1,2,\cdots,n-1
x(1)(t)=[x(0)(1)−a^b^]e−a^(t−1)+a^b^所以x(1)(m+1)=[x(0)(1)−a^b^]e−a^(m)+a^b^,m=1,2,⋯,n−1
由于
x
(
1
)
(
m
)
=
∑
i
=
1
m
x
(
0
)
(
i
)
,
m
=
1
,
2
,
⋯
,
n
x^{(1)}(m)=\displaystyle\sum_{i=1}^{m}x^{(0)}(i),m=1,2,\cdots,n
x(1)(m)=i=1∑mx(0)(i),m=1,2,⋯,n,所以可以得到:
x
(
0
)
(
m
+
1
)
=
x
(
1
)
(
m
+
1
)
−
x
(
1
)
(
m
)
=
(
1
−
e
a
^
)
[
x
(
0
)
(
1
)
−
b
^
a
^
]
e
−
a
^
(
m
)
+
b
^
a
^
,
m
=
1
,
2
,
⋯
,
n
−
1
\bf x^{(0)}(m+1)=x^{(1)}(m+1)-x^{(1)}(m)=(1-e^{\hat a})\left[ x^{(0)}(1)-\frac{\hat b}{\hat a}\right]e^{-\hat a(m)}+\frac{\hat b}{\hat a},\quad m=1,2,\cdots,n-1
x(0)(m+1)=x(1)(m+1)−x(1)(m)=(1−ea^)[x(0)(1)−a^b^]e−a^(m)+a^b^,m=1,2,⋯,n−1
如果对原始数据进行预测,那么只需要在上式 m ≥ n m≥n m≥n 即可。
GM(1,1)模型的本质是有条件的指数拟合: f ( x ) = C 1 e C 2 ( x − 1 ) f(x)=C_1e^{C_2(x-1)} f(x)=C1eC2(x−1),其中这里的指数规律阵对 x ( 1 ) ( k ) x^{(1)}(k) x(1)(k) 序列而言,原始数据是做差的结果。
三、准指数规律的检验
- 数据具有准指数规律是使用灰色系统建模的理论基础。
- 累加 r r r 次的序列为 x ( r ) = ( x ( r ) ( 1 ) , x ( r ) ( 2 ) , ⋯ , x ( r ) ( n ) ) x^{(r)}=(x^{(r)}(1),x^{(r)}(2),\cdots,x^{(r)}(n)) x(r)=(x(r)(1),x(r)(2),⋯,x(r)(n)),定义级比 σ ( k ) = x ( r ) ( k ) x ( r ) ( k − 1 ) , k = 2 , 3 , ⋯ , n \sigma(k)=\frac{x^{(r)}(k)}{x^{(r)}(k-1)},k=2,3,\cdots,n σ(k)=x(r)(k−1)x(r)(k),k=2,3,⋯,n。
- 如果 ∀ k , σ ( k ) ∈ [ a , b ] \forall k,\sigma(k) \in[a,b] ∀k,σ(k)∈[a,b],且区间长度 δ = b − a < 0.5 \delta=b-a<0.5 δ=b−a<0.5,则称累加 r r r 次后的序列具有准指数规律。
- 具体到 GM(1,1) 模型中,我们只需判断累加一次后的序列 x ( 1 ) = ( x ( 1 ) ( 1 ) , x ( 1 ) ( 2 ) , ⋯ , x ( 1 ) ( n ) ) x^{(1)}=(x^{(1)}(1),x^{(1)}(2),\cdots,x^{(1)}(n)) x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n)) 是否存在准指数规律。
- 根据上述公式:
序列 x ( 1 ) x^{(1)} x(1) 的级比 σ ( k ) = x ( 1 ) ( k ) x ( 1 ) ( k − 1 ) = x ( 0 ) ( k ) + x ( 1 ) ( k − 1 ) x ( 1 ) ( k − 1 ) = x ( 0 ) ( k ) x ( 1 ) ( k − 1 ) + 1 \sigma(k)=\frac{x^{(1)}(k)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)+x^{(1)}(k-1)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)}{x^{(1)}(k-1)}+1 σ(k)=x(1)(k−1)x(1)(k)=x(1)(k−1)x(0)(k)+x(1)(k−1)=x(1)(k−1)x(0)(k)+1
定义 ρ ( k ) = x ( 0 ) ( k ) x ( 1 ) ( k − 1 ) \rho(k)=\frac{x^{(0)}(k)}{x^{(1)}(k-1)} ρ(k)=x(1)(k−1)x(0)(k) 为原始序列 x ( 0 ) x^{(0)} x(0) 的光滑比,注意到: ρ ( k ) = x ( 0 ) ( k ) x ( 0 ) ( 1 ) + x ( 0 ) ( 2 ) + ⋯ + x ( 0 ) ( k − 1 ) \rho(k)=\frac{x^{(0)}(k)}{x^{(0)}(1)+x^{(0)}(2)+\cdots+x^{(0)}(k-1)} ρ(k)=x(0)(1)+x(0)(2)+⋯+x(0)(k−1)x(0)(k)
假设 x ( 0 ) x^{(0)} x(0) 为非负序列,那么随着 k k k 增加,最终 ρ ( k ) \rho(k) ρ(k) 会逐渐接近 0,因此要是的具有 x ( 1 ) x^{(1)} x(1) 具有准指数规律,即 ∀ k \forall k ∀k,区间长度 δ \delta δ <0.5,只需要保证 ρ ( k ) ∈ ( 0 , 0.5 ) \rho(k)∈(0,0.5) ρ(k)∈(0,0.5) 即可,此时序列 x ( 1 ) x^{(1)} x(1) 的级比 σ ( k ) ∈ ( 1 , 1.5 ) \sigma(k)∈(1,1.5) σ(k)∈(1,1.5) 。
注意:一般前两期: ρ ( 2 ) \rho(2) ρ(2) 和 ρ ( 3 ) \rho(3) ρ(3) 可能不符合要求,重点关注后面的期数。
四、GM(1,1)模型的评价
使用 GM(1,1) 模型对未来的数据进行预测时,首先需要检验 GM(1,1) 模型对原数据的拟合程度(对原始数据的还原效果)。一般有两种方法:残差检验和级比偏差检验。
残差检验:
绝对残差:
ε
(
k
)
=
x
(
0
)
(
k
)
−
x
^
(
0
)
(
k
)
,
k
=
2
,
3
,
⋯
,
n
\varepsilon(k)=x^{(0)}(k)-\hat x^{(0)}(k),k=2,3,\cdots,n
ε(k)=x(0)(k)−x^(0)(k),k=2,3,⋯,n
相对残差:
ε
r
(
k
)
=
∣
x
(
0
)
−
x
^
(
0
)
(
k
)
∣
x
(
0
)
(
k
)
×
100
%
,
k
=
2
,
3
,
⋯
,
n
\varepsilon_r(k)=\frac{|x^{(0)}-\hat x^{(0)}(k)|}{ x^{(0)}(k)}\times100\%,k=2,3,\cdots,n
εr(k)=x(0)(k)∣x(0)−x^(0)(k)∣×100%,k=2,3,⋯,n
平均相对残差:
ε
‾
r
=
1
n
−
1
∑
k
=
2
n
∣
ε
r
(
k
)
∣
\overline \varepsilon_r = \frac{1}{n-1} \sum_{k=2}^{n}|\varepsilon_r(k)|
εr=n−11k=2∑n∣εr(k)∣
- 如果 ε ‾ r < 20 % \overline \varepsilon_r< 20\% εr<20%,则认为 GM(1,1) 对原始数据的拟合达到了一般要求。
- 如果 ε ‾ r < 10 % \overline \varepsilon_r< 10\% εr<10%,则认为 GM(1,1) 对原始数据的拟合达效果非常不错。(10%不绝对)
级比偏差检验:
首先由
x
(
0
)
(
k
−
1
)
x^{(0)}(k-1)
x(0)(k−1) 和
x
(
0
)
(
k
)
x^{(0)}(k)
x(0)(k) 计算出原始数据的级比
σ
(
k
)
\sigma(k)
σ(k):
σ
(
k
)
=
x
(
0
)
(
k
)
x
(
0
)
(
k
−
1
)
,
(
k
=
2
,
3
,
⋯
,
n
)
\sigma(k)=\frac{x^{(0)}(k)}{x^{(0)}(k-1)},\quad(k=2,3,\cdots,n)
σ(k)=x(0)(k−1)x(0)(k),(k=2,3,⋯,n)
再根据预测出来的发展系数
(
−
a
^
)
(-\hat a)
(−a^) 计算出相应的级比偏差和平均级比偏差:
η
(
k
)
=
∣
1
−
1
−
0.5
a
^
1
+
0.5
a
^
1
σ
(
k
)
∣
,
η
ˉ
=
∑
k
=
2
n
η
(
k
)
n
−
1
\eta(k)=\left|1-\frac{1-0.5\hat a}{1+0.5\hat a}\frac{1}{\sigma(k)}\right|,\quad \bar \eta=\sum_{k=2}^{n}\frac{\eta(k)}{n-1}
η(k)=∣∣∣∣1−1+0.5a^1−0.5a^σ(k)1∣∣∣∣,ηˉ=k=2∑nn−1η(k)
- 如果 η ˉ < 0.2 \bar \eta< 0.2 ηˉ<0.2,则认为 GM(1,1) 对原始数据的拟合达到了一般要求。
- 如果 η ˉ < 0.1 \bar \eta< 0.1 ηˉ<0.1,则认为 GM(1,1) 对原始数据的拟合达效果非常不错。
检验的原理:
η
(
k
)
\eta(k)
η(k) 越小,说明
x
(
0
)
(
k
)
x^{(0)}(k)
x(0)(k) 和
x
^
(
0
)
(
k
)
\hat x^{(0)}(k)
x^(0)(k) 越接近。特别地,当
η
(
k
)
=
0
\eta(k)=0
η(k)=0 时,可以得到:
σ
(
k
)
=
1
−
0.5
a
^
1
+
0.5
a
^
=
x
^
(
0
)
(
k
)
x
(
0
)
(
k
−
1
)
\sigma(k)=\frac{1-0.5\hat a}{1+0.5\hat a}=\frac{\hat x^{(0)}(k)}{x^{(0)}(k-1)}
σ(k)=1+0.5a^1−0.5a^=x(0)(k−1)x^(0)(k)
五、模型扩展(★)
- 数据是以年份度量的非负数据(如果是月份或者季度数据就要用 时间序列模型);
- 数据能经过准指数规律的检验(除了前两期外,后面至少90%的期数的光滑比要低于0.5,规定的 90% 不绝对) ;
- 数据的期数较短且和其他数据之间的关联性不强(小于等于10,也不能太短了,比如只有 3 期数据),要是数据期数较长,一般用传统的时间序列模型比较合适。
- 在传统的 GM(1,1) 模型的基础上,每预测一次,将预测的数据作为已知数据进行下一次预测,那么这种模型为 新信息 GM(1,1) 模型。在新信息 GM(1,1) 模型的基础上,去掉最老信息 x ( 0 ) ( 1 ) x^{(0)}(1) x(0)(1) ,那么这种模型为 新陈代谢 GM(1,1) 模型。应对比传统GM(1,1)、新信息 GM(1,1) 、新陈代谢 GM(1,1) 三种模型的预测效果,抉择使用。
本文借鉴了数学建模清风老师的课件与思路,如果大家发现文章中有不正确的地方,欢迎大家在评论区留言,也可以点击查看下方链接查看清风老师的视频讲解~








 灰色预测模型GM(1,1)是一种处理含有已知和不确定信息系统的预测方法,通过对非负数据序列进行一次累加生成处理,建立微分方程模型进行预测。本文详细介绍了GM(1,1)模型的原理,包括数据生成、模型建立、参数估计和模型评价,并探讨了模型的适用条件和扩展。通过最小二乘法求解模型参数,利用级比偏差和残差检验评估模型拟合效果。在满足特定条件的数据集上,GM(1,1)模型能有效预测未来趋势。
灰色预测模型GM(1,1)是一种处理含有已知和不确定信息系统的预测方法,通过对非负数据序列进行一次累加生成处理,建立微分方程模型进行预测。本文详细介绍了GM(1,1)模型的原理,包括数据生成、模型建立、参数估计和模型评价,并探讨了模型的适用条件和扩展。通过最小二乘法求解模型参数,利用级比偏差和残差检验评估模型拟合效果。在满足特定条件的数据集上,GM(1,1)模型能有效预测未来趋势。


















 12万+
12万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










